Đề thi thử THPT môn Toán năm 2025 Sở GD&ĐT Hà Tĩnh
I. Phần trắc nghiệm
Đề bài
Hàm số nào dưới đây đồng biến trên khoảng \(( - \infty ; + \infty )\)?
-
A.
\(y = - {x^3} - 2x + 1\)
-
B.
\(y = \frac{{x - 2}}{{x + 1}}\)
-
C.
\(y = 3{x^3} + 3x - 2\)
-
D.
\(y = 2{x^3} - 5x + 1\)
Cho hàm số y = f(x) có đạo hàm \(f'(x) = ({x^2} - 4)(x + 2)(x - 3)\) và liên tục trên \(\mathbb{R}\). Số điểm cực trị của hàm số đã cho là
-
A.
5
-
B.
2
-
C.
3
-
D.
1
Cho hàm số y = f (x) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn [-2;4] bằng
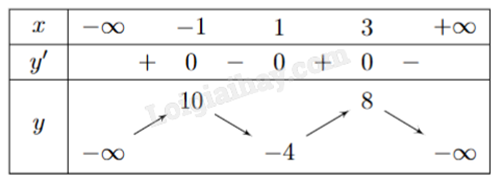
-
A.
-1
-
B.
10
-
C.
1
-
D.
8
Cho hàm số đa thức bậc bốn y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) − 1 = 0 có bao nhiêu nghiệm thực phân biệt?
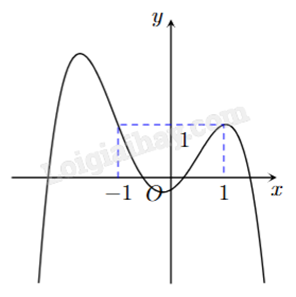
-
A.
3
-
B.
1
-
C.
2
-
D.
4
-
A.
\(y = {x^3} + 3x\)
-
B.
\(y = {x^3} - 3x\)
-
C.
\(y = {x^3} - 3{x^2}\)
-
D.
\(y = {x^3} + 3{x^2}\)
Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^x} < \frac{1}{8}\) là?
-
A.
\((3; + \infty )\)
-
B.
\(( - \infty ;3)\)
-
C.
\([3; + \infty )\)
-
D.
\(( - \infty ;3]\)
Trong không gian Oxyz, cho \(\overrightarrow a = 2\overrightarrow i - 3\overrightarrow j + \overrightarrow k \). Tọa độ của \(\overrightarrow a \) là
-
A.
(-2;1;3)
-
B.
(2;-3;1)
-
C.
(2;1;3)
-
D.
(2;1;-3)
Trong không gian Oxyz, cho tam giác ABC với A(1;3;4), B(2;−1;0), C(3;1;2). Tọa độ trọng tâm G của tam giác ABC là
-
A.
\(G\left( {3;\frac{3}{2};3} \right)\)
-
B.
\(G\left( {2; - 1;2} \right)\)
-
C.
\(G\left( {2;1;2} \right)\)
-
D.
\(G\left( {6;3;6} \right)\)
Trong không gian Oxyz, cho \(\overrightarrow a = (1; - 2;2)\), \(\overrightarrow b = ( - 1;2;1)\). Giá trị của tích vô hướng \(\overrightarrow a .\overrightarrow b \) bằng
-
A.
3
-
B.
-3
-
C.
2
-
D.
-2
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAD đều. Góc giữa hai đường thẳng BC và SA bằng
-
A.
\({60^o}\)
-
B.
\({30^o}\)
-
C.
\({90^o}\)
-
D.
\({45^o}\)
Trong tuẫn lễ bảo vệ môi trường, các học sinh khối 12 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 12 ở bảng sau:

Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.
-
A.
19,51
-
B.
19,59
-
C.
20,1
-
D.
18,3
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{x}\) \((ac \ne 0)\) có đồ thị như hình vẽ. Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng
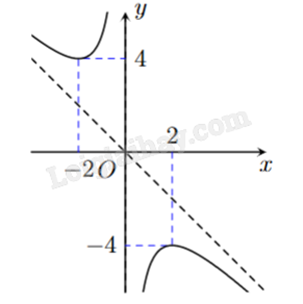
-
A.
Đường thẳng y = x
-
B.
Đường thẳng y = -x
-
C.
Đường thẳng x = 0
-
D.
Đường thẳng y = 2x
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức \(c(t) = \frac{t}{{{t^2} + 1}}\) (mg/l).
a) Sau khi tiêm thuốc 2 giờ thì nồng độ thuốc trong máu của bệnh nhân bằng 0,4 (mg/l).
b) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân có thể vượt quá 0,5 (mg/l).
c) Sau khi tiêm thuốc 1 giờ thì nồng độ thuốc trong máu của bệnh nhân cao nhất.
d) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân cao nhất bằng 0,5 (mg/l).
Một hồ nước nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh hoạ, nó được giới hạn bởi các trục tọa độ và đồ thị của hàm số \(y = f(x) = - 0,1{x^3} + 0,9{x^2} - 1,5x + 5,6\). Đơn vị đo độ dài trên mỗi trục tọa độ là 100m.
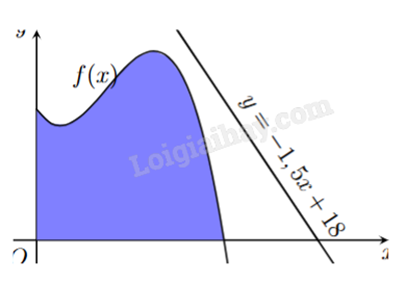
a) Đường dạo ven hồ chạy dọc theo trục Ox dài 600m.
b) Trên đường đi dạo ven hồ chạy dọc theo trục Ox, điểm cách gốc O một đoạn 500m có khoảng cách theo phương thẳng đứng đến bờ hồ đối điện là lớn nhất.
c) Khoảng cách nhỏ nhất theo phương thẳng đứng từ một điểm trên đường đi dạo ven hồ đến bờ hồ đối diện là 490 m.
d) Trong công viên có một con đường chạy dọc theo đồ thị hàm số y = −1,5x + 18. Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyền đến con đường này là ngắn nhất. Biết toạ độ của điểm để xây bến thuyền này là M(a;b). Giá trị a + 5b bằng 43.
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1;0;−2), B(−2;3;4), C(4;−6;1).
a) \(\overrightarrow {AB} = (3; - 3;6)\).
b) Hình chiếu vuông góc của B lên trục Ox là B′(−2;3;0).
c) Tồn tại 1 điểm M thuộc trục hoành sao cho tam giác MBC vuông tại M.
d) Nếu ABDC là hình bình hành thì tọa độ điểm D là (1;−3;7).
Cho lăng trụ đứng ABC.A’B’C’ có AC = a, BC = 2a, \(\widehat {ACB} = {120^o}\) có thể tích V. Gọi M là trung điểm của BB’.
a) Góc phẳng nhị diện \([A,CC.,B] = {60^o}\).
b) Biết khoảng cách giữa hai mặt đáy lăng trụ bằng 2a. Khi đó \(V = {a^3}\sqrt 3 \).
c) \({V_{M.ABC}} = \frac{1}{6}V\).
d) \(d(C',(ABB'A')) = \frac{{a\sqrt {21} }}{7}\).
Cho đồ thị hàm số f (x) = 2sinx như hình vẽ bên. Tính diện tích tam giác ABC (kết quả làm tròn đến hàng phần trăm).
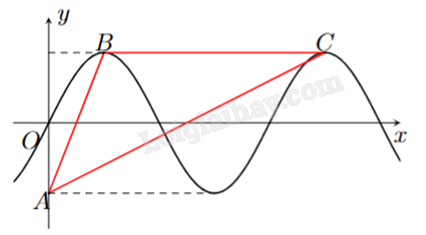
Đáp án:
Trong đề kiểm tra 15 phút môn Toán có 20 câu trắc nghiệm. Mỗi câu trắc nghiệm có 4 phương án trả lời, trong đó chỉ có một phương án trả lời đúng. An giải chắc chắn đúng 10 câu, 10 câu còn lại lựa chọn ngẫu nhiên đáp án. Biết rằng mỗi câu trả lời đúng được 0,5 điểm, trả lời sai không bị trừ điểm. Xác suất để An đạt được đúng 8 điểm là p. Khi đó, 100p bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Một hồ bơi được chế tạo từ một khối hộp chữ nhật có chiều dài 12 mét, rộng 6 mét, sâu 1 mét ở đầu
nông và sâu 3 mét ở đầu sâu (như hình vẽ). Nước được bơm vào hồ bơi với tốc độ 0,25 mét khối mỗi phút. Biết rằng trong bể có 1 mét nước ở đầu sâu. Để lượng nước đạt 75% dung tích bể bơi thì cần bơm trong thời gian bao lâu (đơn vị tính bằng phút)?
Đáp án:
Giả sử tỉ lệ sinh của tỉnh A tuân theo quy luật logistic được mô hình hoá bằng hàm số \(f(t) = \frac{{200}}{{1 + 4{e^{ - t}}}}\), \(t \ge 0\), \(t \in \mathbb{N}\), trong đó thời gian t được tính bằng tháng. Khi đó đạo hàm f’(t) sẽ biểu thị tốc độ tăng dân số của tỉnh A. Hỏi sau bao nhiêu tháng tốc độ tăng trưởng của dân số tỉnh A là lớn nhất?
Đáp án:
Một máy bay trình diễn có đường bay gắn với hệ trục Oxy được mô phỏng như hình vẽ, trục Ox gắn với mặt đất. Đường bay có dạng là một phần của đồ thị hàm phân thức bậc hai trên bậc nhất y = f (x) có đường tiệm cận đứng là x = 2. Điểm G là giao điểm của đường tiệm cận xiên của đồ thị hàm y = f (x) và trục Ox được gọi là điểm giới hạn. Biết rằng máy bay xuất phát tại vị trí A cách gốc toạ độ O một khoảng 2,5 đơn vị và máy bay khi ở vị trí cao nhất cách điểm xuất phát 1,5 đơn vị theo phương song song với trục Ox và cách mặt đất 4,5 đơn vị. Vị trí máy bay tiếp đất cách điểm giới hạn một khoảng bằng bao nhiêu?
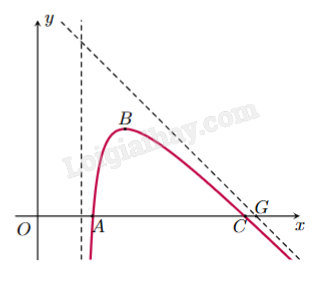
Đáp án:
Có ba lực cùng tác động vào một cái bàn như hình vẽ. Trong đó hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) có giá nằm trên mặt phẳng chứa mặt bàn, tạo với nhau một góc \({110^o}\) và có độ lớn lần lượt là 9N và 4N , lực \(\overrightarrow {{F_2}} \) vuông góc với mặt bàn và có độ lớn 7N. Độ lớn hợp lực của ba lực trên là a(N), tìm giá trị của a (kết quả quy tròn về số nguyên).
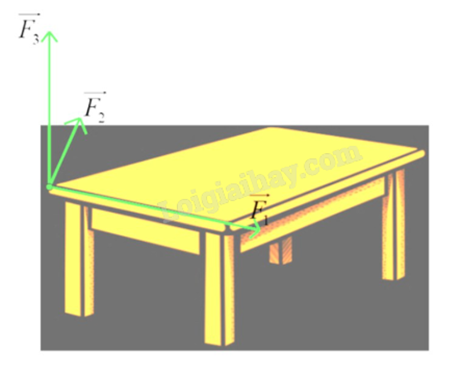
Đáp án:
Lời giải và đáp án
Hàm số nào dưới đây đồng biến trên khoảng \(( - \infty ; + \infty )\)?
-
A.
\(y = - {x^3} - 2x + 1\)
-
B.
\(y = \frac{{x - 2}}{{x + 1}}\)
-
C.
\(y = 3{x^3} + 3x - 2\)
-
D.
\(y = 2{x^3} - 5x + 1\)
Đáp án : C
Tính đạo hàm của từng hàm số rồi xét sự biến thiên.
Xét đáp án A: \(y' = - 3{x^2} - 2 < 0\), \(\forall x \in \mathbb{R}\) nên hàm số nghịch biến trên \(\mathbb{R}\). Loại A.
Xét đáp án B: Hàm số không liên tục trên \(\mathbb{R}\). Loại B.
Xét đáp án C: \(y' = 9{x^2} + 3 > 0\), \(\forall x \in \mathbb{R}\) nên hàm số đồng biến trên \(\mathbb{R}\). Chọn C.
Xét đáp án D: \(y' = 6{x^2} - 5 = 0 \Leftrightarrow \pm \frac{{\sqrt {30} }}{6}\) nên hàm số không đồng biến trên \(\mathbb{R}\). Loại D.
Cho hàm số y = f(x) có đạo hàm \(f'(x) = ({x^2} - 4)(x + 2)(x - 3)\) và liên tục trên \(\mathbb{R}\). Số điểm cực trị của hàm số đã cho là
-
A.
5
-
B.
2
-
C.
3
-
D.
1
Đáp án : B
Lập bảng biến thiên và xét dấu.
Ta có bảng xét dấu:

Vậy f(x) có hai điểm cực trị là x = 2 và x = 3.
Cho hàm số y = f (x) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn [-2;4] bằng

-
A.
-1
-
B.
10
-
C.
1
-
D.
8
Đáp án : B
Quan sát bảng biến thiên và nhận xét.
Quan sát bảng biến thiên, ta thấy giá trị lớn nhất của f(x) trên [-2;4] là f(-1) = 10.
Cho hàm số đa thức bậc bốn y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) − 1 = 0 có bao nhiêu nghiệm thực phân biệt?

-
A.
3
-
B.
1
-
C.
2
-
D.
4
Đáp án : A
Cho hàm số y = f(x) có đồ thị \(({C_1})\) và y = g(x) có đồ thị \(({C_2})\).
Số giao điểm của \(({C_1})\) và \(({C_2})\) bằng số nghiệm của phương trình f(x) = g(x).
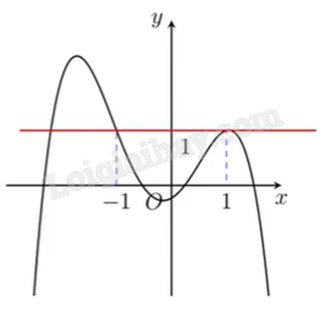
\(f(x) - 1 = 0 \Leftrightarrow f(x) = 1\).
Đồ thị hàm số f(x) cắt đường thẳng y = 1 tại ba điểm nên phương trình trên có ba nghiệm thực phân biệt.
-
A.
\(y = {x^3} + 3x\)
-
B.
\(y = {x^3} - 3x\)
-
C.
\(y = {x^3} - 3{x^2}\)
-
D.
\(y = {x^3} + 3{x^2}\)
Đáp án : C
Thay tọa độ các điểm thuộc đồ thị vào từng hàm số xem có thỏa mãn phương trình.
\(f( - 1) = 2\) nên loại A, D.
\(f(2) = 4\) nên loại B.
Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^x} < \frac{1}{8}\) là?
-
A.
\((3; + \infty )\)
-
B.
\(( - \infty ;3)\)
-
C.
\([3; + \infty )\)
-
D.
\(( - \infty ;3]\)
Đáp án : A
Với 0 < a < 1, ta có \({a^x} < {a^\alpha } \Leftrightarrow x > \alpha \).
\({\left( {\frac{1}{2}} \right)^x} < \frac{1}{8} \Leftrightarrow {\left( {\frac{1}{2}} \right)^x} < {\left( {\frac{1}{2}} \right)^x} \Leftrightarrow x > 3\) (vì \(0 < \frac{1}{2} < 1\)).
Trong không gian Oxyz, cho \(\overrightarrow a = 2\overrightarrow i - 3\overrightarrow j + \overrightarrow k \). Tọa độ của \(\overrightarrow a \) là
-
A.
(-2;1;3)
-
B.
(2;-3;1)
-
C.
(2;1;3)
-
D.
(2;1;-3)
Đáp án : B
\(\overrightarrow a = m\overrightarrow i + n\overrightarrow j + p\overrightarrow k = (m;n;p)\).
\(\overrightarrow a = 2\overrightarrow i - 3\overrightarrow j + \overrightarrow k = (2; - 3;1)\).
Trong không gian Oxyz, cho tam giác ABC với A(1;3;4), B(2;−1;0), C(3;1;2). Tọa độ trọng tâm G của tam giác ABC là
-
A.
\(G\left( {3;\frac{3}{2};3} \right)\)
-
B.
\(G\left( {2; - 1;2} \right)\)
-
C.
\(G\left( {2;1;2} \right)\)
-
D.
\(G\left( {6;3;6} \right)\)
Đáp án : C
Với G là trọng tâm tam giác ABC, ta có \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3}\end{array} \right.\).
\(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 2 + 3}}{3} = 2\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{3 + ( - 1) + 1}}{2} = 1\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{4 + 0 + 2}}{3} = 2\end{array} \right. \Rightarrow G(2;1;2)\).
Trong không gian Oxyz, cho \(\overrightarrow a = (1; - 2;2)\), \(\overrightarrow b = ( - 1;2;1)\). Giá trị của tích vô hướng \(\overrightarrow a .\overrightarrow b \) bằng
-
A.
3
-
B.
-3
-
C.
2
-
D.
-2
Đáp án : B
Áp dụng biểu thức tọa độ của tích vô hướng: \(\overrightarrow a .\overrightarrow b = {x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}\).
\(\overrightarrow a .\overrightarrow b = 1.( - 1) + ( - 2).2 + 2.1 = - 3\).
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAD đều. Góc giữa hai đường thẳng BC và SA bằng
-
A.
\({60^o}\)
-
B.
\({30^o}\)
-
C.
\({90^o}\)
-
D.
\({45^o}\)
Đáp án : A
Nếu a // b thì (a,c) = (b,c).

ABCD là hình vuông nên BC // AD.
Khi đó \((BC,SA) = (AD,SA) = \widehat {SAD} = {60^o}\) (vì tam giác SAD đều).
Trong tuẫn lễ bảo vệ môi trường, các học sinh khối 12 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 12 ở bảng sau:

Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.
-
A.
19,51
-
B.
19,59
-
C.
20,1
-
D.
18,3
Đáp án : B
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.({u_{m + 1}} - {u_m})\).
Cỡ mẫu: n = 53 + 82 + 48 + 39 + 18 = 240.
Trung vị của dãy số liệu \({x_1},{x_2},...,{x_{240}}\) là \(\frac{{{x_{120}} + {x_{121}}}}{2} \in [15,5;20,5]\).
Số trung vị của mẫu số liệu ghép nhóm là:
\({M_e} = 15,5 + \frac{{\frac{{240}}{2} - 53}}{{82}}(20,5 - 15,5) \approx 19,59\).
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{x}\) \((ac \ne 0)\) có đồ thị như hình vẽ. Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng

-
A.
Đường thẳng y = x
-
B.
Đường thẳng y = -x
-
C.
Đường thẳng x = 0
-
D.
Đường thẳng y = 2x
Đáp án : B
Dựa vào các điểm thuộc đồ thị để tìm hàm số, từ đó tìm đường tiệm cận xiên.
\(y(2) = - 4 \Leftrightarrow \frac{{a{{.2}^2} + b.2 + c}}{2} = - 4 \Leftrightarrow 4a + 2b + c = - 8\) (1).
\(y(2) = 4 \Leftrightarrow \frac{{a{{.2}^2} + b.2 + c}}{2} = 4 \Leftrightarrow 4a - 2b + c = - 8\) (2).
\(y = \frac{{a.{x^2} + b.x + c}}{x} = ax + b + \frac{c}{x}\), suy ra \(y' = a - \frac{c}{{{x^2}}}\).
Ta có \(y'(2) = 0 \Leftrightarrow a - \frac{c}{{{a^2}}} = 0 \Leftrightarrow 4a - c = 0\) (3).
Giải hệ các phương trình (1), (2), (3) ta được a = -1, b = 0, c = -4.
Do đó \(y = \frac{{ - {x^2} - 4}}{x} = - x - \frac{4}{x}\).
\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {f(x) - ( - x)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \left[ { - x - \frac{4}{x} - ( - x)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{ - 4}}{x} = 0\).
Vậy đường tiệm cận xiên là y = -x.
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức \(c(t) = \frac{t}{{{t^2} + 1}}\) (mg/l).
a) Sau khi tiêm thuốc 2 giờ thì nồng độ thuốc trong máu của bệnh nhân bằng 0,4 (mg/l).
b) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân có thể vượt quá 0,5 (mg/l).
c) Sau khi tiêm thuốc 1 giờ thì nồng độ thuốc trong máu của bệnh nhân cao nhất.
d) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân cao nhất bằng 0,5 (mg/l).
a) Sau khi tiêm thuốc 2 giờ thì nồng độ thuốc trong máu của bệnh nhân bằng 0,4 (mg/l).
b) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân có thể vượt quá 0,5 (mg/l).
c) Sau khi tiêm thuốc 1 giờ thì nồng độ thuốc trong máu của bệnh nhân cao nhất.
d) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân cao nhất bằng 0,5 (mg/l).
Tính đạo hàm của hàm số đã cho, lập bảng biến thiên và nhận xét.
a) Đúng. \(c(2) = \frac{2}{{{2^2} + 1}} = 0,4\) (mg/l).
Vậy sau khi tiêm thuốc 2 giờ, nồng độ thuốc trong máu của bệnh nhân bằng 0,4 (mg/l).
b) Sai. Với \(t \ge 0\), ta có \(c'(t) = \frac{{1.({t^2} + 1) - t.2t}}{{{{({t^2} + 1)}^2}}} = \frac{{ - {t^2} + 1}}{{{{({t^2} + 1)}^2}}} = 0 \Rightarrow t = 1\).
Bảng biến thiên:
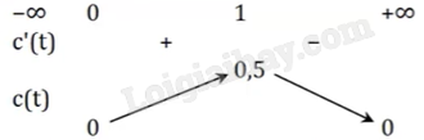
Từ đó, ta thấy với \(t \in [0; + \infty )\) thì \(0 \le c(t) \le 5\) nên nồng độ thuốc trong máu của bệnh nhân không vượt quá 0,5 (mg/l).
c) Đúng. Từ bảng biến thiên, ta thấy nồng độ thuốc trong máu cao nhất bằng c(1) = 0,5 (mg/l).
Vậy sau khi tiêm thuốc 1 giờ thì nồng độ thuốc trong máu của bệnh nhân cao nhất.
d) Đúng. Từ bảng biến thiên, ta thấy nồng độ thuốc trong máu cao nhất bằng 0,5 (mg/l).
Một hồ nước nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh hoạ, nó được giới hạn bởi các trục tọa độ và đồ thị của hàm số \(y = f(x) = - 0,1{x^3} + 0,9{x^2} - 1,5x + 5,6\). Đơn vị đo độ dài trên mỗi trục tọa độ là 100m.

a) Đường dạo ven hồ chạy dọc theo trục Ox dài 600m.
b) Trên đường đi dạo ven hồ chạy dọc theo trục Ox, điểm cách gốc O một đoạn 500m có khoảng cách theo phương thẳng đứng đến bờ hồ đối điện là lớn nhất.
c) Khoảng cách nhỏ nhất theo phương thẳng đứng từ một điểm trên đường đi dạo ven hồ đến bờ hồ đối diện là 490 m.
d) Trong công viên có một con đường chạy dọc theo đồ thị hàm số y = −1,5x + 18. Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyền đến con đường này là ngắn nhất. Biết toạ độ của điểm để xây bến thuyền này là M(a;b). Giá trị a + 5b bằng 43.
a) Đường dạo ven hồ chạy dọc theo trục Ox dài 600m.
b) Trên đường đi dạo ven hồ chạy dọc theo trục Ox, điểm cách gốc O một đoạn 500m có khoảng cách theo phương thẳng đứng đến bờ hồ đối điện là lớn nhất.
c) Khoảng cách nhỏ nhất theo phương thẳng đứng từ một điểm trên đường đi dạo ven hồ đến bờ hồ đối diện là 490 m.
d) Trong công viên có một con đường chạy dọc theo đồ thị hàm số y = −1,5x + 18. Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyền đến con đường này là ngắn nhất. Biết toạ độ của điểm để xây bến thuyền này là M(a;b). Giá trị a + 5b bằng 43.
a) Tìm hoành độ giao điểm của đồ thị f(x) và trục hoành.
b) Tìm giá trị lớn nhất của hàm số f(x) trên khoảng hoặc đoạn phù hợp.
c) Tìm giá trị nhỏ nhất của hàm số f(x) trên khoảng hoặc đoạn phù hợp.
d) Áp dụng công thức tính khoảng cách và ứng dụng đạo hàm để tìm giá trị nhỏ nhất.
a) Sai. Hoành độ giao điểm của f(x) và trục Ox là nghiệm của phương trình:
\( - 0,1{x^3} + 0,9{x^2} - 1,5x + 5,6 = 0 \Leftrightarrow x = 8\).
Vậy đường dạo ven hồ chạy dọc theo trục Ox dài 800m.
b) Đúng. \(f'(x) = - 0,3{x^2} + 1,8x - 1,5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 5\end{array} \right.\).
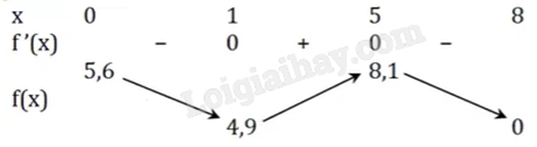
Vậy điểm cách O một đoạn 500m có khoảng cách theo phương thẳng dứng đến bờ hồ đối diện là lớn nhất và bằng 810m.
c) Đúng. Khoảng cách nhỏ nhất theo phương thẳng đứng từ một điểm trên đường đi dạo ven hồ đến bờ hồ đối diện là f(1) = 490m.
d) Đúng. Gọi \(M(a;b) \in f(x)\) với \(0 \le x \le 8\). Khi đó \(M(a; - 0,1{a^3} + 0,9{a^2} - 1,5a + 5,6)\).
Đặt \(\Delta :y = - 1,5 + 18 \Leftrightarrow 1,5x + y - 18 = 0\).
\(d(M,\Delta ) = \frac{{\left| {1,5a + \left( { - 0,1{a^3} + 0,9{a^2} - 1,5a + 5,6} \right) + 18} \right|}}{{\sqrt {1,{5^2} + {1^2}} }} = \frac{{2\sqrt {13} }}{{13}}\left| { - 0,1{a^3} + 0,9{a^2} + 12,4} \right|\).
Xét hàm \(f(a) = - 0,1{a^3} + 0,9{a^2} + 12,4\) với \(0 \le x \le 8\).
\(f'(a) = - 0,3{x^2} + 1,8a = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\a = 6\end{array} \right.\).
Bảng biến thiên:
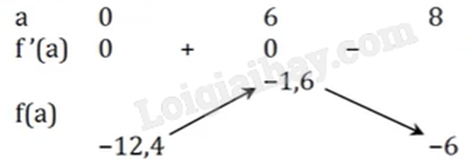
Với \(0 \le x \le 8\) thì \( - 12,4 \le f(a) \le - 1,6\) suy ra \(1,6 \le \left| {f(a)} \right| \le 12,4\).
Vậy giá trị nhỏ nhất của |f(a)| khi \(0 \le x \le 8\) là |f(6)| = 1,6.
Suy ra \(\min d(M,\Delta ) = \frac{{2\sqrt {13} }}{{13}}.1,6 = \frac{{16\sqrt {13} }}{{65}}\) khi a = 6. Khi đó M(6;7,4).
Vậy a + 5b = 6 + 5.7,4 = 43.
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1;0;−2), B(−2;3;4), C(4;−6;1).
a) \(\overrightarrow {AB} = (3; - 3;6)\).
b) Hình chiếu vuông góc của B lên trục Ox là B′(−2;3;0).
c) Tồn tại 1 điểm M thuộc trục hoành sao cho tam giác MBC vuông tại M.
d) Nếu ABDC là hình bình hành thì tọa độ điểm D là (1;−3;7).
a) \(\overrightarrow {AB} = (3; - 3;6)\).
b) Hình chiếu vuông góc của B lên trục Ox là B′(−2;3;0).
c) Tồn tại 1 điểm M thuộc trục hoành sao cho tam giác MBC vuông tại M.
d) Nếu ABDC là hình bình hành thì tọa độ điểm D là (1;−3;7).
a) Áp dụng công thức tính tọa độ vecto \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\).
b) Hình chiếu vuông góc của điểm A(a;b;c) lên trục Ox là A’(a;0;0).
c) Áp dụng công thức tính tích vô hướng cho hai vecto vuông góc.
d) Áp dụng quy tắc về hai vecto bằng nhau.
a) Sai. \(\overrightarrow {AB} = ( - 2 - 1;3 - 0;4 + 2) = ( - 3;3;6)\).
b) Sai. Hình chiếu vuông góc của B lên trục Ox là B’(-2;0;0).
c) Sai. \(M \in Ox \Rightarrow M(x;0;0)\).
\(\overrightarrow {BM} = (x + 2; - 3; - 4)\), \(\overrightarrow {CM} = (x - 4;6; - 1)\).
\(\Delta MBC\) vuông tại M suy ra \(\overrightarrow {BM} .\overrightarrow {CM} = 0 \Leftrightarrow (x + 2)(x - 4) + ( - 3).6 + ( - 4).( - 1) = 0 \Leftrightarrow {x^2} - 2x - 22 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt {23} \\x = 1 - \sqrt {23} \end{array} \right.\).
Vậy có hai điểm M thỏa mãn là \({M_1}(1 + \sqrt {23} ;0;0)\) và \({M_2}(1 - \sqrt {23} ;0;0)\).
d) Đúng. \(\overrightarrow {BD} = ({x_D} + 2;{y_D} - 3;{z_D} - 4)\), \(\overrightarrow {AC} = (3; - 6;3)\).
ABDC là hình bình hành \( \Leftrightarrow \overrightarrow {BD} = \overrightarrow {AC} \Leftrightarrow \left\{ \begin{array}{l}{x_D} + 2 = 3\\{y_D} - 3 = - 6\\{z_D} - 4 = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 1\\{y_D} = - 3\\{z_D} = 7\end{array} \right.\).
Vậy D(1;-3;7).
Cho lăng trụ đứng ABC.A’B’C’ có AC = a, BC = 2a, \(\widehat {ACB} = {120^o}\) có thể tích V. Gọi M là trung điểm của BB’.
a) Góc phẳng nhị diện \([A,CC.,B] = {60^o}\).
b) Biết khoảng cách giữa hai mặt đáy lăng trụ bằng 2a. Khi đó \(V = {a^3}\sqrt 3 \).
c) \({V_{M.ABC}} = \frac{1}{6}V\).
d) \(d(C',(ABB'A')) = \frac{{a\sqrt {21} }}{7}\).
a) Góc phẳng nhị diện \([A,CC.,B] = {60^o}\).
b) Biết khoảng cách giữa hai mặt đáy lăng trụ bằng 2a. Khi đó \(V = {a^3}\sqrt 3 \).
c) \({V_{M.ABC}} = \frac{1}{6}V\).
d) \(d(C',(ABB'A')) = \frac{{a\sqrt {21} }}{7}\).
a) Góc phẳng nhị diện của góc nhị diện là góc có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.
b) Áp dụng công thức tính diện tích tam giác \(S = \frac{1}{2}bc\sin A\) và công thức tính thể tích lăng trụ \(V = Bh\).
c) Dựa vào tỉ lệ độ dài giữa đoạn MB và BB’.
d) Tìm hình chiếu vuông góc của điểm lên mặt phẳng rồi tính khoảng cách giữa điểm đó và hình chiếu.
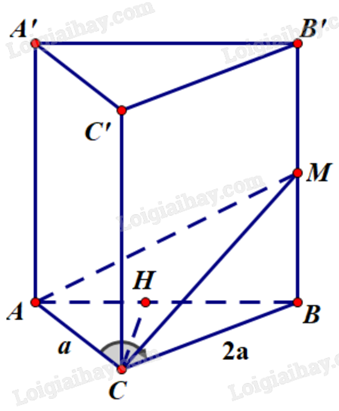
a) Sai. Có \(\left\{ \begin{array}{l}AC \bot CC'\\BC \bot CC'\end{array} \right. \Rightarrow [a;CC';B] = (AC,BC) = \widehat {ACB} = {120^o}\).
b) Đúng. \({S_{ABC}} = \frac{1}{2}AC.BC.\sin \widehat {ACB} = \frac{1}{2}a.2a.\sin {120^o} = \frac{{{a^2}\sqrt 3 }}{2}\).
\(V = {S_{ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{2}.2a = {a^3}\sqrt 3 \).
c) Đúng. \({V_{MABC}} = \frac{1}{3}MB.{S_{ABC}} = \frac{1}{3}.\frac{1}{2}AA'.{S_{ABC}} = \frac{1}{6}V\).
d) Đúng. Gọi H là đường cao của tam giác ABC.
Ta có \(\left\{ \begin{array}{l}CH \bot AB\\AA' \bot (ABC) \Rightarrow AA' \bot CH\end{array} \right. \Rightarrow CH \bot (AA'B'B) \Rightarrow d(C,(ABB'A')) = CH\).
\(AB = \sqrt {A{C^2} + B{C^2} - 2AC.BC.\cos \widehat {ACB}} = \sqrt {{a^2} + {{(2a)}^2} - 2.a.2a.\cos {{120}^o}} = a\sqrt 7 \).
\({S_{ABC}} = \frac{1}{2}CH.AB \Leftrightarrow \frac{{{a^2}\sqrt 3 }}{2} = \frac{1}{2}CH.a\sqrt 7 \Leftrightarrow CH = \frac{{a\sqrt {21} }}{7}\).
Vì CC’ // (ABB’A”) nên \(d(C',(ABB'A')) = d(C,(ABB'A')) = CH = \frac{{a\sqrt {21} }}{7}\).
Cho đồ thị hàm số f (x) = 2sinx như hình vẽ bên. Tính diện tích tam giác ABC (kết quả làm tròn đến hàng phần trăm).

Đáp án:
Đáp án:
Tìm tọa độ các điểm A, B, C rồi tính diện tích tam giác.
Với mọi \(x \in \mathbb{R}\), ta có: \( - 1 \le \sin x \le 1 \Leftrightarrow - 2 \le 2\sin x \le 2 \Leftrightarrow - 2 \le f(x) \le 2\).
Xét \(f(x) = 2 \Leftrightarrow 2\sin x = 2 \Leftrightarrow \sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \) \((k \in \mathbb{Z})\).
Với x > 0, ta có: \(\frac{\pi }{2} + k2\pi > 0 \Leftrightarrow k2\pi > - \frac{\pi }{2} \Leftrightarrow k > - \frac{1}{4} \Rightarrow k \in \{ 0;1;2...\} \).
Dựa vào đồ thị, ta thấy:
Với k = 0 thì \(x = \frac{\pi }{2} + 0.2\pi = \frac{\pi }{2}\). Vậy \(B\left( {\frac{\pi }{2};2} \right)\).
Với k = 1 thì \(x = \frac{\pi }{2} + 1.2\pi = \frac{{5\pi }}{2}\). Vậy \(C\left( {\frac{{5\pi }}{2};2} \right)\).
Có A(0;-2).
\(BC = \sqrt {{{(2\pi )}^2} + {0^2}} = 2\pi \).
\(d(A,BC) = 2OA = 2.2 = 4\).
\({S_{ABC}} = \frac{1}{2}d(A,BC).BC = \frac{1}{2}.4.2\pi = 4\pi \approx 12,57\).
Trong đề kiểm tra 15 phút môn Toán có 20 câu trắc nghiệm. Mỗi câu trắc nghiệm có 4 phương án trả lời, trong đó chỉ có một phương án trả lời đúng. An giải chắc chắn đúng 10 câu, 10 câu còn lại lựa chọn ngẫu nhiên đáp án. Biết rằng mỗi câu trả lời đúng được 0,5 điểm, trả lời sai không bị trừ điểm. Xác suất để An đạt được đúng 8 điểm là p. Khi đó, 100p bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Đáp án:
Tìm số câu hỏi mà An cần chọn đúng và cần chọn sai để đạt đúng 8 điểm.
Áp dụng công thức tổ hợp để tính xác suất.
Để đạt được đúng 8 điểm thì An phải trả lời đúng 16 câu và sai 4 câu. Khi đó, số câu chọn ngẫu nhiên đúng là 6 câu và sai là 4 câu.
Số cách chọn 6 câu đúng từ 10 câu chọn ngẫu nhiên là \(C_{10}^6\).
Số cách chọn 4 câu sai từ 4 câu chọn ngẫu nhiên còn lại là \(C_4^4\).
Xác suất để chọn 1 câu đúng là \(\frac{1}{4}\), xác suất để chọn 1 câu sai là \(\frac{3}{4}\).
Vậy xác suất để chọn 6 câu đúng và 4 câu sai từ 10 câu chọn ngẫu nhiên còn lại là \(p = C_{10}^6.C_4^4.{\left( {\frac{1}{4}} \right)^6}.{\left( {\frac{3}{4}} \right)^4} = \frac{{17010}}{{1048576}}\).
Vậy \(100p \approx 1,6\).
Một hồ bơi được chế tạo từ một khối hộp chữ nhật có chiều dài 12 mét, rộng 6 mét, sâu 1 mét ở đầu
nông và sâu 3 mét ở đầu sâu (như hình vẽ). Nước được bơm vào hồ bơi với tốc độ 0,25 mét khối mỗi phút. Biết rằng trong bể có 1 mét nước ở đầu sâu. Để lượng nước đạt 75% dung tích bể bơi thì cần bơm trong thời gian bao lâu (đơn vị tính bằng phút)?
Đáp án:
Đáp án:
Sử dụng công thức tính diện tích hình thang và thể tích hình lăng trụ đứng.
Áp dụng hệ quả định lí Thales.
Tính thể tích phần nước đã có trong bể, thể tích toàn bộ bể rồi từ đó tìm ra thể tích nước cần bơm.
Đặt tên các điểm như hình vẽ.
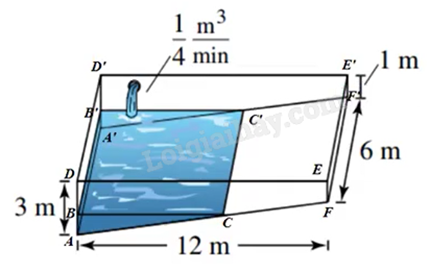
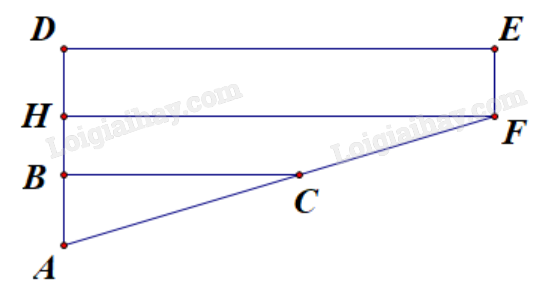
Ta có \(AD = AB + HB + DH\)
\( \Leftrightarrow HB = AD - AB - DH = 3 - 1 - 1 = 1\) (m).
Suy ra \(AH = AB + BH = 1 + 1 = 2\).
Sử dụng hệ quả định lí Thales, ta có:
\(\frac{{BC}}{{HF}} = \frac{{AB}}{{AH}} \Leftrightarrow BC = \frac{{AB.HF}}{{AH}} = \frac{{AB.DE}}{{AH}} = \frac{{1.12}}{2} = 6\) (m).
\({S_{ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}.1.6 = 3\) \(({m^2})\).
Thể tích nước đang có trong bể là: \({V_1} = {S_{ABC}}.AA' = 3.6 = 18\) \(({m^3})\).
\({S_{ADEF}} = \frac{{(AD + EF).DE}}{2} = \frac{{(3 + 1).12}}{2} = 24\) \(({m^2})\).
Thể tích hồ bơi là: \(V = {S_{ADEF}}.AA' = 24.6 = 144\) \(({m^3})\).
Thể tích nước cần bơm là: \(75\% V - {V_1} = 75\% .144 - 18 = 90\) \(({m^3})\).
Thời gian bơm là: \(\frac{{96}}{{0,25}} = 360\) (phút).
Giả sử tỉ lệ sinh của tỉnh A tuân theo quy luật logistic được mô hình hoá bằng hàm số \(f(t) = \frac{{200}}{{1 + 4{e^{ - t}}}}\), \(t \ge 0\), \(t \in \mathbb{N}\), trong đó thời gian t được tính bằng tháng. Khi đó đạo hàm f’(t) sẽ biểu thị tốc độ tăng dân số của tỉnh A. Hỏi sau bao nhiêu tháng tốc độ tăng trưởng của dân số tỉnh A là lớn nhất?
Đáp án:
Đáp án:
Tính đạo hàm cấp hai của f(t), từ đó tìm giá trị lớn nhất của f’(t).
\(f'(t) = 200.\frac{{ - 4{e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^2}}} = \frac{{800{e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^2}}}\);
\(f''(t) = 800.\frac{{ - {e^{ - t}}{{(1 + 4{e^{ - t}})}^2} - {e^{ - t}}.2.( - 4{e^{ - t}}).(1 + 4{e^{ - t}})}}{{{{(1 + 4{e^{ - t}})}^4}}} = 800.\frac{{4{{({e^{ - t}})}^2} - {e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^3}}} = \frac{{800{e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^3}}}(4{e^{ - t}} - 1)\).
\(f''(t) = 0 \Leftrightarrow 4{e^{ - t}} - 1 = 0 \Leftrightarrow \ln {e^{ - t}} = \ln \frac{1}{4} \Leftrightarrow - t\ln e = \ln 1 - \ln 4 \Leftrightarrow - t = 0 - \ln 4 \Leftrightarrow t = \ln 4\).
Bảng biến thiên:
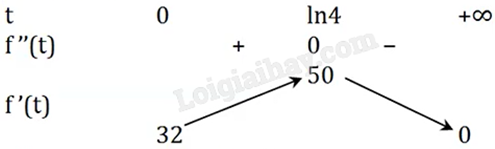
Giá trị lớn nhất của f’(t) là f’(ln4) = 50.
Tốc độ tăng trưởng dân số của tỉnh A lớn nhất bằng 50 khi \(t = \ln 4 \approx 1,38\).
\(f'(1) \approx 48,18\); \(f'(2) \approx 45,57\). Suy ra f’(1) > f’(2).
Vậy sau 1 tháng, tốc độ tăng trưởng dân số của tỉnh A là lớn nhất.
Một máy bay trình diễn có đường bay gắn với hệ trục Oxy được mô phỏng như hình vẽ, trục Ox gắn với mặt đất. Đường bay có dạng là một phần của đồ thị hàm phân thức bậc hai trên bậc nhất y = f (x) có đường tiệm cận đứng là x = 2. Điểm G là giao điểm của đường tiệm cận xiên của đồ thị hàm y = f (x) và trục Ox được gọi là điểm giới hạn. Biết rằng máy bay xuất phát tại vị trí A cách gốc toạ độ O một khoảng 2,5 đơn vị và máy bay khi ở vị trí cao nhất cách điểm xuất phát 1,5 đơn vị theo phương song song với trục Ox và cách mặt đất 4,5 đơn vị. Vị trí máy bay tiếp đất cách điểm giới hạn một khoảng bằng bao nhiêu?

Đáp án:
Đáp án:
Dựa vào các điểm đồ thị đi qua và điểm cực trị, tìm phương trình của đồ thị biểu diễn đường bay.
Từ đó, tìm tọa độ giao điểm C với trục Ox, phương trình đường tiệm cận xiên và tọa độ điểm G là giao điểm của tiệm cận xiên với trục Ox.
Tính khoảng cách CG.
Đường bay là một phần của đồ thị hàm số bậc hai trên bậc nhất: \(y = \frac{{a{x^2} + bx + c}}{{x - 2}}\) (do tiệm cận đứng là x = 2).
Theo đề bài: A(2,5;0), B(4;4,5).
Vì A thuộc đồ thị hàm số nên ta có \(\frac{{a.2,{5^2} + b.2,5 + c}}{{2,5 - 2}} = 0 \Leftrightarrow 6,25a + 2,5b + c = 0\) (1).
Vì B thuộc đồ thị hàm số nên ta có \(\frac{{a{{.4}^2} + b.4 + c}}{{4 - 2}} = 4,5 \Leftrightarrow 16a + 4b + c = 9\) (2).
\(y' = \frac{{(2ax + b)(x - 2) - (a{x^2} + bx + c).1}}{{{{(x - 2)}^2}}} = \frac{{a{x^2} - 4ax - 2b - c}}{{{{(x - 2)}^2}}}\).
Điểm B là một cực trị của đồ thị hàm số nên \(\frac{{a{{.4}^2} - 4a.4 - 2b - c}}{{{{(4 - 2)}^2}}} = 0 \Leftrightarrow 2b + c = 0\) (3).
Giải hệ các phương trình (1), (2), (3), ta được a = -1; b = 12,5; c = -25.
Suy ra \(y = f(x) = \frac{{ - {x^2} + 12,5x - 25}}{{x - 2}} = - x + 10,5 - \frac{4}{{x - 2}}\).
\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {f(x) - ( - x + 10,5)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \left[ { - x + 10,5 + \frac{4}{{x - 2}} - ( - x + 10,5)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \frac{4}{{x - 2}} = 0\).
Vậy y = -x + 10,5 là tiệm cận xiên.
Phương trình hoành độ giao điểm của tiệm cận xiên và trục Ox là \( - x + 10,5 = 0 \Leftrightarrow x = 10,5\).
Vậy G(10,5;0).
Phương trình hoành độ giao điểm của đồ thị f(x) với trục Ox là \(\frac{{ - {x^2} + 12,5x - 25}}{{x - 2}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2,5\\x = 10\end{array} \right.\).
Vậy A(2,5;0), C(10;0).
\(CG = {x_G} - {x_C} = 10,5 - 10 = 0,5\).
Vậy vị trí máy bay tiếp đất tại C cách điểm giới hạn G một khoảng bằng 0,5.
Có ba lực cùng tác động vào một cái bàn như hình vẽ. Trong đó hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) có giá nằm trên mặt phẳng chứa mặt bàn, tạo với nhau một góc \({110^o}\) và có độ lớn lần lượt là 9N và 4N , lực \(\overrightarrow {{F_2}} \) vuông góc với mặt bàn và có độ lớn 7N. Độ lớn hợp lực của ba lực trên là a(N), tìm giá trị của a (kết quả quy tròn về số nguyên).

Đáp án:
Đáp án:
Sử dụng quy tắc tổng hợp lực \(\overrightarrow {{F_{12}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) và \({F_{12}} = \sqrt {{F_1}^2 + {F_2}^2 + 2{F_1}.{F_2}\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right)} \).
\(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right| = \sqrt {{{\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right)}^2}} \)
\( = \sqrt {{F_1}^2 + {F_2}^2 + {F_3}^2 + 2\overrightarrow {{F_1}} .\overrightarrow {{F_2}} + 2\overrightarrow {{F_2}} .\overrightarrow {{F_3}} + 2\overrightarrow {{F_3}} .\overrightarrow {{F_1}} } \)
\( = \sqrt {{F_1}^2 + {F_2}^2 + {F_3}^2 + 2{F_1}.{F_2}.\cos {{110}^o} + 2{F_2}.{F_3}.\cos {{90}^o} + 2{F_3}.{F_1}.\cos {{90}^o}} \)
\( = \sqrt {{9^2} + {4^2} + {7^2} + 2.9.4\cos {{110}^o} + 2.4.7.\cos {{90}^o} + 2.7.9.\cos {{90}^o}} \approx 11\) (N).
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2026 trường THPT Cửa Lò - Nghệ An
Đề KSCL Toán 12 lần 1 năm 2025 - 2026 trường THPT Triệu Sơn 3 - Thanh Hóa
Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng
Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình
Đề thi thử THPT môn Toán năm 2026 trường THPT Nguyễn Trung Thiên - Hà Tĩnh
Các bài khác cùng chuyên mục
- Đề thi thử THPT môn Toán năm 2026 trường THPT Nguyễn Trung Thiên - Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình
- Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
- Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
- Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng
- Đề thi thử THPT môn Toán năm 2026 trường THPT Nguyễn Trung Thiên - Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình
- Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
- Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
- Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng









Danh sách bình luận