Hàm số nào dưới đây đồng biến trên khoảng \(( - \infty ; + \infty )\)?
-
A.
\(y = - {x^3} - 2x + 1\)
-
B.
\(y = \frac{{x - 2}}{{x + 1}}\)
-
C.
\(y = 3{x^3} + 3x - 2\)
-
D.
\(y = 2{x^3} - 5x + 1\)
Tính đạo hàm của từng hàm số rồi xét sự biến thiên.
Xét đáp án A: \(y' = - 3{x^2} - 2 < 0\), \(\forall x \in \mathbb{R}\) nên hàm số nghịch biến trên \(\mathbb{R}\). Loại A.
Xét đáp án B: Hàm số không liên tục trên \(\mathbb{R}\). Loại B.
Xét đáp án C: \(y' = 9{x^2} + 3 > 0\), \(\forall x \in \mathbb{R}\) nên hàm số đồng biến trên \(\mathbb{R}\). Chọn C.
Xét đáp án D: \(y' = 6{x^2} - 5 = 0 \Leftrightarrow \pm \frac{{\sqrt {30} }}{6}\) nên hàm số không đồng biến trên \(\mathbb{R}\). Loại D.
Đáp án : C

Các bài tập cùng chuyên đề
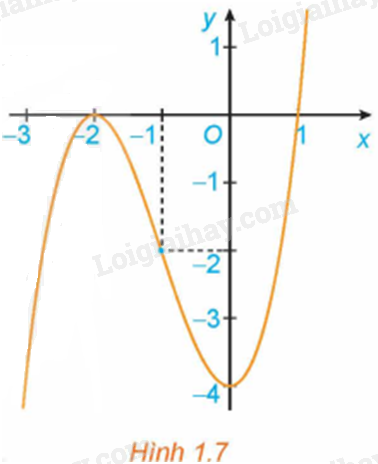
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
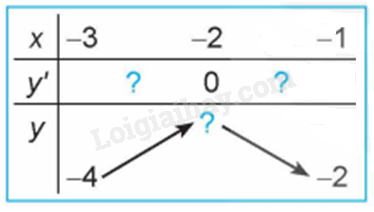
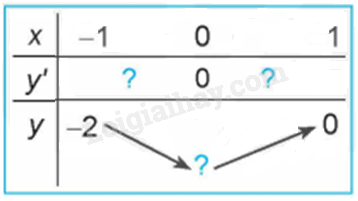
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\);
b) \(y = - {x^3} + 2{x^2} - 5x + 3\).
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{{2x - 1}}{{x + 2}}\);
b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Xét chiều biến thiên của các hàm số sau:
a) \(y = \sqrt {4 - {x^2}} \);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
A. \(y = - {x^3} + 3{x^2} - 9x\);
B. \(y = - {x^3} + x + 1\);
C. \(y = \frac{{x - 1}}{{x - 2}}\);
D. \(y = 2{x^2} + 3x + 2\).
Dân số của một quốc gia sau t (năm) kể từ năm 2023 được ước tính bởi công thức: \(N\left( t \right) = 100{e^{0,012t}}\) (N(t) được tính bằng triệu người, \(0 \le t \le 50\)).
a) Ước tính dân số của quốc gia này vào các năm 2030 và 2035 (kết quả tính bằng triệu người, làm tròn kết quả đến chữ số thập phân thứ ba).
b) Xem N(t) là hàm số của biến số t xác định trên đoạn [0; 50]. Xét chiều biến thiên của hàm số N(t) trên đoạn [0; 50].
c) Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/ năm). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm?
Tìm các khoảng đơn điệu của hàm số sau \(y = \frac{{2x - 1}}{{x + 2}}\).
Chứng minh rằng hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
a) Xác định tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^3}\).
b) Xét dấu của đạo hàm \(f'\left( x \right) = 3{x^2}\).
c) Phương trình \(f'\left( x \right) = 0\) có bao nhiêu nghiệm ?
Tìm các khoảng đơn điệu của hàm số \(y = {x^4} + 2{x^2} - 3\).
Xét dấu \(y'\) rồi tìm khoảng đồng biến, nghịch biến của hàm số\(y = \frac{4}{3}{x^3} - 2{x^2} + x - 1\).
Tìm các khoảng đơn điệu của hàm số sau:
a) \(y = - {x^3} + 2{x^2} - 3\) b) \(y = {x^4} - 2{x^2} + 5\)
c) \(y = \frac{{3x + 1}}{{2 - x}}\) d) \(y = \frac{{{x^2} - 2x}}{{x + 1}}\)
Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) được tính bởi công thức sau:
\(V\left( T \right) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}\).
Hỏi thể tích \(V\left( T \right)\),\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) giảm trong khoảng nhiệt độ nào?
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm \(t = 0\left( s \right)\) cho đến khi tên lửa đẩy được phóng đi tại thời điểm \(t = 126\left( s \right)\), cho bởi hàm số sau:
\(v\left( t \right) = 0,001320{t^3} - 0,09029{t^2} + 23\).
(v được tính bằng ft/s, 1 feet = 0,3048 m)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\). Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?

Chứng minh rằng hàm số \(f\left( x \right) = 3x - sinx\) đồng biến trên \(\mathbb{R}\)
Xét tính đơn điệu của các hàm số sau:
a) \(f(x) = {x^3} - 6{x^2} + 9x\)
b) \(g(x) = \frac{1}{x}\)
Cho hàm số y = f(x) = \({x^2}\)
a) Từ đồ thị của hàm số y = f(x) (Hình 4), hãy chỉ ra các
khoảng đồng biến và nghịch biến của hàm số đã cho.
b) Tính đạo hàm f '(x) và xét dấu f '(x).
c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến,
nghịch biến của hàm số với dấu của f '(x).

Chứng minh rằng hàm số \(y = \frac{{2x + 1}}{{x - 3}}\) nghịch biến trên từng khoảng xác định của nó
Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức \(f\left( x \right) = 0,01{x^3}-0,04{x^2} + 0,25x + 0,44\) (tỉ USD) với x là số năm tính từ 2010 đến 2017 (\(0 \le x \le 7\)).
a) Tính đạo hàm của hàm số y = f(x).
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Xét một chất điểm chuyển động dọc theo trục \(Ox\). Toạ độ của chất điểm tại thời điểm \(t\) được xác định bởi hàm số \(x(t) = {t^3} - 6{t^2} + 9t\) với \(t \ge 0\). Khi đó \(x'(t)\) là vận tốc của chất điểm tại thời điểm \(t\), kí hiệu \(v(t)\); \(v'(t)\) là gia tốc chuyển động của chất điểm tại thời điểm \(t\), kí hiệu \(a(t)\).
a) Tìm các hàm \(v(t)\) và \(a(t)\).
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Đạo hàm của hàm số y = f (x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng

A. (–1;3)
B. (–3;1)
C. (1;5)
D. (3;\( + \infty \))
Cho hàm \(y = \frac{{ - 2x - 3}}{{4 - x}}\). Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đồng biến trên (\( - \infty \); –4) và nghịch biến trên (–4; \( + \infty \)).
B. Hàm số đồng biến trên (\( - \infty \); 4) và (4; \( + \infty \)).
C. Hàm số nghịch biến trên (\( - \infty \); 4) và (4; \( + \infty \)).
D. Hàm số nghịch biến trên (\( - \infty \); –4) và (–4; \( + \infty \)).
Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau: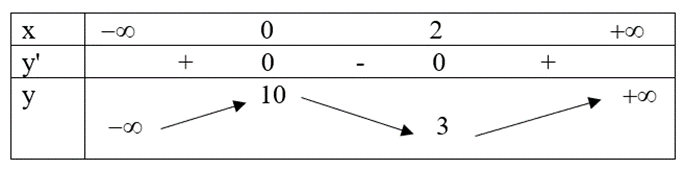
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
-
A.
\(( - \infty ;0)\)
-
B.
\((0;2)\)
-
C.
\((2; + \infty )\)
-
D.
\(\mathbb{R}\)
Hàm số nào sau đây nghịch biến trên R?
-
A.
\(y = \frac{{x - 3}}{{x + 2}}\)
-
B.
\(y = {x^3} - 3x - 5\)
-
C.
\(y = - {x^3} - 2x - 5\)
-
D.
\(y = {x^2} + 4\)
Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:
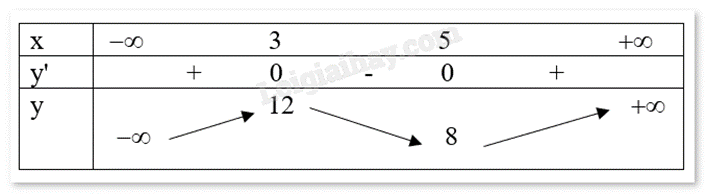
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
-
A.
\(( - \infty ;3)\)
-
B.
\((5; + \infty )\)
-
C.
\((3;5)\)
-
D.
\(\mathbb{R}\)
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?
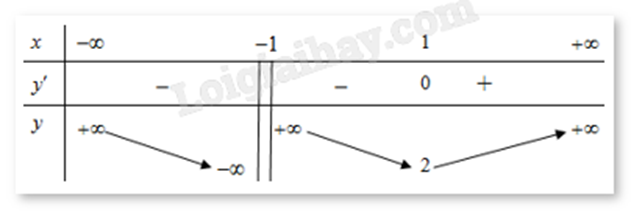
-
A.
Hàm số nghịch biến trên \(( - \infty ; - 1)\)
-
B.
Hàm số nghịch biến trên \(( - \infty ; + \infty )\)
-
C.
Hàm số đồng biến trên khoảng \(( - 1; + \infty )\)
-
D.
Hàm số đồng biến trên khoảng \(( - \infty ;1)\)
Hình 1.2 là đồ thị (C) của hàm số \(y = f(x) = \frac{{ - 1}}{2}{x^2} + 3\)
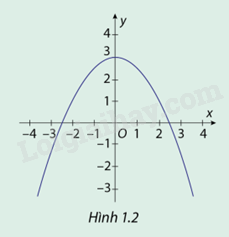
a) Quan sát đồ thị hàm số (C) và chỉ ra các khoảng đồng biến, nghịch biến của hàm số đã cho.
b) Xác định dấu của đạo hàm \(f'(x)\) khi \(x\)thuộc các khoảng đồng biến, nghịch biến ở câu.
c) Ghi lại và hoàn thành bảng biến thiên sau
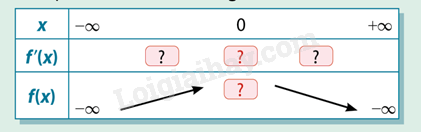
Lập bảng biến thiên và kết luận các khoảng đồng biến, nghịch biến của hàm số.
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Cho hàm số \(y = f(x) = {x^3} + 1\)
a) Bằng định nghĩa, hãy cho biết hàm \(f(x)\)có đồng biến trên \(R\) hay không
b) Hãy nhận xét về dấu của đạo hàm \(f'(x)\) trên \(R\)







Danh sách bình luận