Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAD đều. Góc giữa hai đường thẳng BC và SA bằng

Kim tự tháp Cheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay). (Theo britannica.com).

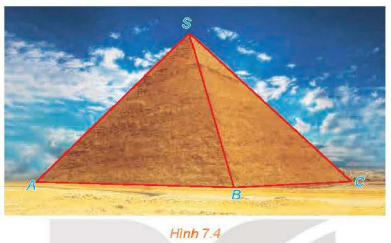
Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp (H.7.4).

Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) và (a', b') có mối quan hệ gì?

Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).

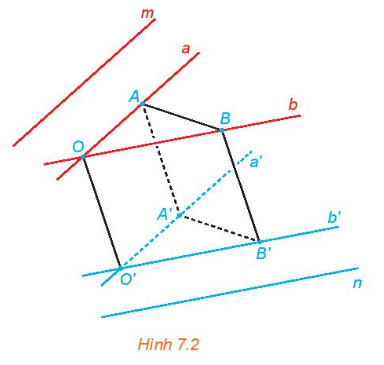
a) Mỗi cặp đường thẳng a, a và b, b' có cùng thuộc một mặt phẳng hay không?

b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B' Giải thích vì sao OAA'O', OBB'O', ABB'A' là các hình bình hành.

c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.

(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B').

Đối với hai cánh cửa trong Hình 7.5, tính góc giữa hai đường mép cửa BC và MN.

Cho hình lăng trụ ABC.A'B'C' có các đáy là các tam giác đều. Tính góc (AB, B'C'). 

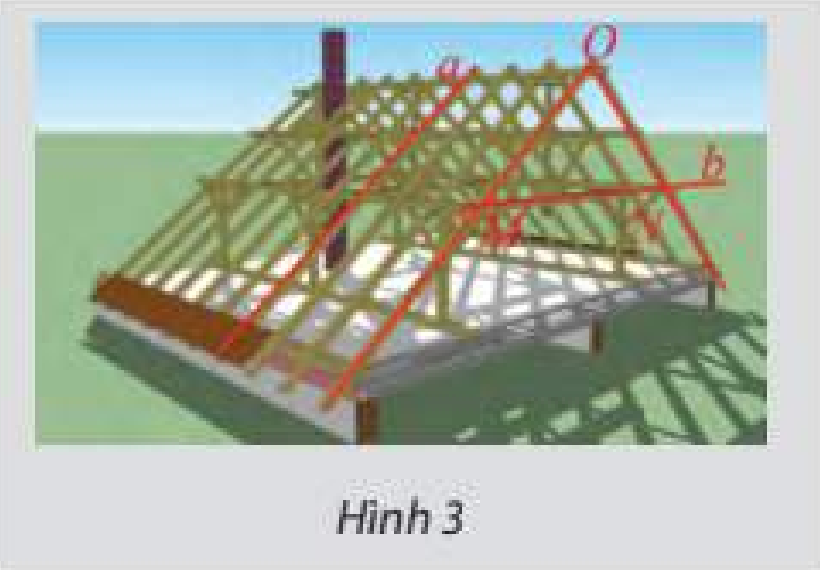
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác \(OMN\) vuông cân tại \(O\). Tính góc giữa hai thanh gỗ \(a\) và \(b\).

Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông  \(M,N,E,F\) lần lượt là trung điểm các cạnh \(BC,BA,AA',A'D'\). Tính góc giữa các cặp đường thẳng:

a) \(MN\) và \(DD'\);            

b) \(MN\) và \(CD'\);            

c) \(EF\) và \(CC'\).

Cho hai đường thẳng chéo nhau \(a\) và \(b\) trong không gian. Qua một điểm \(M\) tuỳ ý vẽ \(a'\parallel a\) và vẽ \(b'\parallel b\). Khi thay đổi vị trí của điểm \(M\), có nhận xét gì về góc giữa \(a'\) và \(b'\)?

Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:

a) \(AB\) và \(BB'\);

b) \(AB\) và \(DD'\).

Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).

Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(K\) là trung điểm của \(CD\). Tính góc giữa hai đường thẳng \(AK\) và \(BC\).

Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(BC\) và \(A{\rm{D}}\). Biết \(AB = CD = 2a\) và \(MN = a\sqrt 3 \). Tính góc giữa \(AB\) và \(C{\rm{D}}\).

Một ô che nắng có viền khung hình lục giác đều \(ABCDEF\) song song với mặt bàn và có cạnh \(AB\) song song với cạnh bàn \(a\) (Hình 5). Tinh số đo góc hợp bởi đường thẳng \(a\) lần lượt với các đường thẳng \(AF,AE\) và \(A{\rm{D}}\).

Cho đường thẳng \(d\) vuông góc với hai đường thẳng 2 cắt nhau \(a\) và \(b\) trong mặt phẳng \(\left( P \right)\). Xét một đường thẳng \(c\) bất kì trong \(\left( P \right)\) (\(c\) không song song với \(a\) và \(b\)). Gọi \(O\) là giao điểm của \(d\) và \(\left( P \right)\). Trong \(\left( P \right)\) vẽ qua \(O\) ba đường thẳng \(a',b',c'\) lần lượt song song với \(a,b,c\). Vẽ một đường thẳng cắt \(a',b',c'\) lần lượt tại \(B,C,D\). Trên \(d\) lấy hai điểm \(E,F\) sao cho \(O\) là trung điểm của \(EF\) (Hình 4).

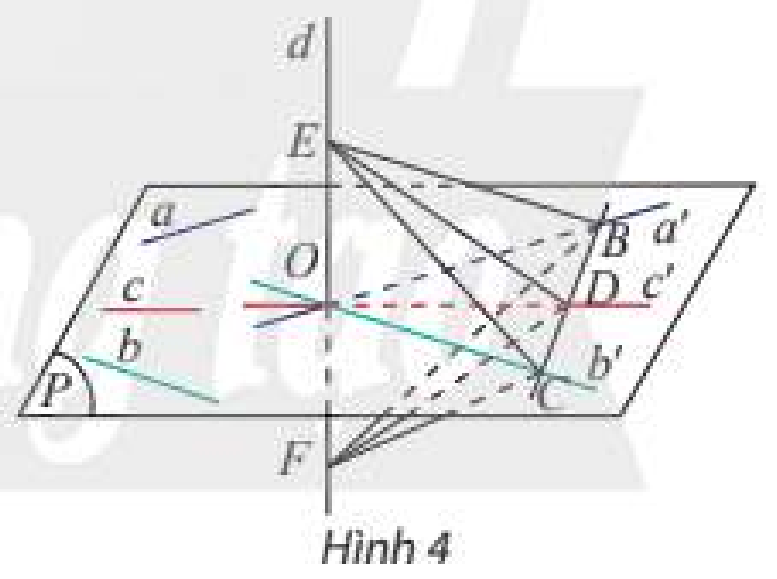
a) Giải thích tại sao hai tam giác \(CEB\) và \(CFB\) bằng nhau.

b) Có nhận xét gì về tam giác \(DEF\)? Từ đó suy ra góc giữa \(d\) và \(c\).

Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam giác MNP đều. Tính góc giữa hai đường thẳng AC và BD.

Trong mặt phẳng cho hai đường thẳng a, b.

a) Nếu a và b cắt nhau tại O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?

b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?

c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = 100^\circ \) (Hình 8) . Tính góc giữa hai đường thẳng: 

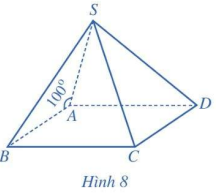
a) SA và AB.

b) SA và CD.

Quan sát Hình 32 và cho biết:

a) Hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng nào.

b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc nào.

Giả sử ở những giây đầu tiên sau khi cất cánh. máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc \({20^ \circ }\) và có vận tốc 200 km/h. Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 2 giây (làm tròn kết quả đến hàng phần mười).

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAD là tam giác đều và M là trung điểm của cạnh AD. Tính góc giữa hai đường thẳng BC và SA, BC và SM.

Cho hình hộp ABCD có tất cả các cạnh bằng nhau và góc A’AD bằng 120 độ. Tính góc giữa các cặp đường thẳng sau: A’C và BD, AD và BB’, A’D và BB’.

Cho hình chóp S.ABCD có đáy là hình vuông tâm O và tất cả các cạnh của hình chóp đều bằng a. Gọi M, N lần lượt là trung điểm các cạnh SA, AB.

a) Tính góc giữa các cặp đường thẳng sau: MN và SD, MO và SB.

b) Tính tang của góc giữa hai đường thẳng SN và BC.

Một chiếc thang có dạng hình thang cân cao 6 m, hai chân thang cách nhau 80 cm, hai ngọn thang cách nhau 60 cm.Thang được dựa vào bờ tường như hình bên. Tính góc tạo giữa đường thẳng chân tường và cạnh cột thang (tính gần đúng theo đơn vị độ, làm tròn kết quả đến chữ số thập phân thứ hai).

Cho đường thẳng a vuông góc với mặt phẳng (P), đường thẳng b song song với mặt phẳng (P). Góc giữa hai đường thẳng a và b bằng

A. \({30^ \circ }\).

B. \({90^ \circ }\).

C. \({60^ \circ }\).

D. \({0^ \circ }\).

Cho tứ diện đều ABCD, góc giữa hai đường thẳng AB và CD bằng

A. \({30^0}\).

B. \({45^0}\).

C. \({60^0}\).

D. \({90^0}\).

Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM.

Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(SA = a\sqrt 3 ,SA \bot AC,\) \(SA \bot BC,\) \(\widehat {BAD} = {120^0}\). Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:

a) SD và BC.

b) MN và SC.

Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính các góc giữa các đường thẳng sau:

a) IJ và DC.

b) MN và IJ.

Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) vuông góc với nhau, giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) là đường thẳng \(c\). Gọi a là đường thẳng nằm trên \(\left( P \right)\) và vuông góc với đường thẳng \(c;b\) là đường thẳng nằm trên \(\left( Q \right)\) và tạo với đường thẳng \(c\) một góc \({60^ \circ }\). Góc giữa hai đường thẳng \(a\) và \(b\) bằng

A. \({60^ \circ }\).

B. \({90^ \circ }\).

C. \({150^ \circ }\).

D. \({30^ \circ }\).

Cho hình lập phương \(ABCD \cdot A'B'C'D'\) có cạnh bằng \(a\). Góc giữa hai đường thẳng \(AC\) và \(BC'\) bằng

A. \({90^ \circ }\).

B. \({30^ \circ }\).

C. \({60^ \circ }\).

D. \({45^ \circ }\).