Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 2 - Hình học 7
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 2 - Hình học 7
Đề bài
Bài 1. Cho biết \( \Rightarrow \widehat {{A_1}} + \widehat {BAD} + \widehat {{A_3}} = {90^o}\) \(\Delta ABC = \Delta HIK\), trong đó có \(AC = 5cm\), \(\widehat A = {70^o},\,\widehat C = {50^o}\). Tính HK và số đo góc I của tam giác HIK.
Bài 2. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC. Tia phân giác của góc \(\widehat {HAB}\) cắt BC tại E, tia phân giác của góc \(\widehat {HAC}\) cắt BC tại D. Chứng minh rằng \(AB + AC = BC + DE.\)
Bài 3. Cho tam giác ABC có ba góc nhọn, kẻ BD vuông góc với AC (D thuộc AC) và CE vuông góc với AB (E thuộc AB). Trên tia đối của tia BD lấy điểm F sao cho \(BF = AC\). Trên tia đối của tia CE lấy điểm G sao cho \(CG = AB.\)
a) Chứng minh \(\widehat {ABF} = \widehat {ACG}\).
b) Chứng minh \(AF = AG\) và \(AF \bot AG.\)
LG bài 1
Phương pháp giải:
Sử dụng:
Tính chất 2 tam giác bằng nhau
Tổng ba góc của 1 tam giác bằng 180 độ
Lời giải chi tiết:
\(\Delta ABC = \Delta HIK\)(giả thiết) \( \Rightarrow HK = AC = 5cm.\)
\(\widehat {HIK} = \widehat {ABC} = {180^o} - \left( {\widehat A + \widehat C} \right) \)\(\;= {180^o} - \left( {{{70}^o} + {{50}^o}} \right) = {60^o}\).
\(\widehat {AEC} = \widehat {{A_2}} + \widehat {HAC}\), mà \(\widehat {{A_1}} = \widehat {{A_2}}\) (giả thiết)
LG bài 2
Phương pháp giải:
Sử dụng:
Hai góc cùng phụ với góc thứ 3 thì bằng nhau
Góc ngoài của tam giác bằng tổng 2 góc trong không kề với nó
Tổng ba góc của 1 tam giác bằng 180 độ
Tam giác cân có 2 cạnh bên bằng nhau
Lời giải chi tiết:
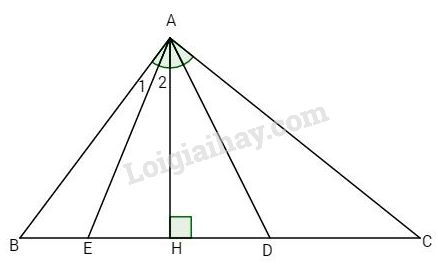
Ta có \(\widehat {AEH} = \widehat B + \widehat {{A_1}}\) (góc ngoài của \(\Delta AEB\)
\(\widehat B = \widehat {HAC}\) (cùng phụ với góc C)
\( \Rightarrow \widehat {AEC} = \widehat {EAC} \Rightarrow \Delta AEC\) cân tại C
\( \Rightarrow AC = EC.\)
Chứng minh tương tự ta lại có \(\Delta ABD\) cân tại B \( \Rightarrow AB = BD.\)
Từ đó vế trái: \(AB + AC = BD + CE \)\(\;= BD + ED + DC;\)
Vế phải: \(BC + DE = BD + DC + DE.\)
Vậy \(AB + AC = BC + DE\,(đpcm)\).
LG bài 3
Phương pháp giải:
Sử dụng:
Hai góc cùng phụ với góc thứ 3 thì bằng nhau
Tổng 2 góc kề bù bằng 180 độ
Lời giải chi tiết:
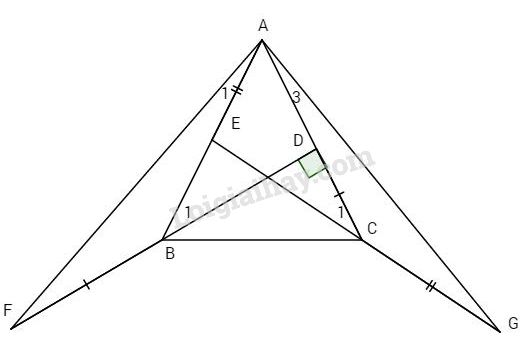
a) Ta có \(\widehat {{B_1}} = \widehat {{C_1}}\) (cùng phụ với góc \(\widehat {BAC}\)), mà \(\widehat {{B_1}} + \widehat {ABF} = {180^o}\) (kề bù).
Tương tự \(\widehat {{C_1}} + \widehat {ACG} = {180^o} \Rightarrow \widehat {ABF} = \widehat {ACG}.\)
b) Xét \(\Delta ABF\) và \(\Delta GCA\) có
+) \(AB = CG\) (giả thiết)
+) \(\widehat {ABF} = \widehat {ACG}\) (chứng minh trên)
+) \(BF = AC\) (giả thiết).
Do đó \(\Delta ABF = \Delta GCA\)(c.g.c)
\( \Rightarrow AF = AG.\)
Ta có \(\Delta ADF\) vuông tại D (giả thiết) nên \(\widehat {{A_1}} + \widehat {BAD} + \widehat F = {90^o}\)
Mà \(\widehat F = \widehat {{A_3}}\,(\Delta ABF = \Delta GCA)\)
\( \Rightarrow \widehat {{A_1}} + \widehat {BAD} + \widehat {{A_3}} = {90^o}\) hay \(AF \bot AG.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 2 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 2 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 2 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 2 - Hình học 7
- Lý thuyết Ôn tập chương 2. Tam giác
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
