Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Ôn tập chương III : Quan hệ giữa các yếu tố trong tam g..
Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 3 - Hình học 7
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 3 - Hình học 7
Đề bài
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH, các đường phân giác của góc \(\widehat {BAH}\) và \(\widehat {CAH}\) cắt BC ở D và E.
a) Chứng minh \(\widehat {HAB} = \widehat {C.}\)
b) Chứng minh \(\Delta ABE\) cân.
Bài 2: Cho tam giác ABC có \(AB < AC\), phân giác AD. Trên tia AC lấy điểm E sao cho \(A{\rm{E}} = AB.\)
a) Chứng minh: \(B{\rm{D}} = E{\rm{D}}.\)
b) AB cắt ED ở K. Chứng minh rằng: \(\Delta DBK = \Delta DEC.\)
c) Chứng minh: \(\Delta AKC\) cân tại A.
d) Chứng minh: \(A{\rm{D}} \bot KC.\)
LG bài 1
Phương pháp giải:
+Tổng hai góc nhọn trong tam giác vuông bằng 90 độ
+Hai góc cùng phụ với góc thứ ba thì bằng nhau
Lời giải chi tiết:
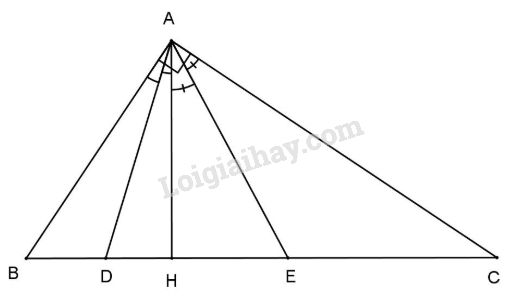
a) Ta có \(\Delta ABC\) vuông tại A nên \(\widehat B + \widehat C = {90^0}\) (1) (trong tam giác vuông, 2 góc nhọn có tổng bằng \(90^0\))
\(\Delta AHB\) vuông tại H nên
\(\widehat B + \widehat {BAC} = {90^0}\) (2) (trong tam giác vuông, 2 góc nhọn có tổng bằng \(90^0\))
Từ (1) và (2) \( \Rightarrow \widehat {BAH} = \widehat C\) (cùng phụ với góc B)
b) Mặt khác AE là tia phân giác của \(\widehat {A{\rm{E}}B} = \widehat C + \widehat {CA{\rm{E}}}\) (góc ngoài \(\Delta A{\rm{E}}C\))
\( \Rightarrow \widehat {BAH} + \widehat {HA{\rm{E}}} = \widehat {A{\rm{E}}B}\) hay \(\widehat {E{\rm{A}}B} = \widehat {A{\rm{E}}B}.\)
Chứng tỏ \(\Delta ABE\) cân tại B.
LG bài 2
Phương pháp giải:
Hai góc kề bù có tổng bằng 180 độ
Hai góc đối đỉnh thì bằng nhau
Trong tam giác cân đường trung tuyến đồng thời là đường cao
Lời giải chi tiết:
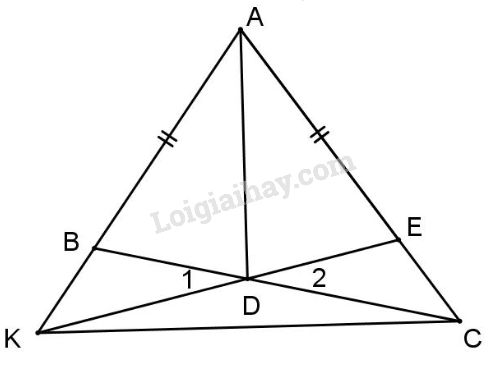
a) Xét \(\Delta A{\rm{D}}B\) và \(\Delta A{\rm{D}}E\) có:
+) AD cạnh chung;
+) \({\widehat A_1} = {\widehat A_2}\) (gt);
+) \(AB = A{\rm{E}}\) (gt).
Do đó \(\Delta A{\rm{D}}B = \Delta A{\rm{D}}E\) (c.g.c)
b) \(\Delta A{\rm{D}}B = \Delta A{\rm{D}}E\)(cmt)
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {A{\rm{ED}}}\) (góc tương ứng),
mà \(\widehat {AB{\rm{D}}} + \widehat {A{\rm{ED}}} = {180^0}\) (kề bù).
Tương tự \(\widehat {A{\rm{ED}}} + \widehat {CE{\rm{D}}} = {180^0}\)
\( \Rightarrow \widehat {BK{\rm{D}}} = \widehat {CE{\rm{D}}}.\)
Xét \(\Delta KB{\rm{D}}\) và \(\Delta CE{\rm{D}}\) có:
+) \({\widehat D_1} = {\widehat D_2}\) (đối đỉnh);
+) DB = DE (cmt);
+) \(\widehat {K{\rm{D}}B} = \widehat {CE{\rm{D}}}\) (cmt).
Do đó \(\Delta DBK = \Delta DEC\) (g.c.g).
c) Ta có \(AB = A{\rm{E}}\) (gt), \(\Delta \Delta {\rm B}{\rm K} = \Delta DEC\) (cmt) \( \Rightarrow BK = EC\) (cmt) \( \Rightarrow AB + BK = A{\rm{E}} + EC\) hay \(AK = AC.\)
Vậy \(\Delta AKC\) cân tại A.
d) \(\Delta ABC\) cân tại A (cmt); có AD là phân giác (gt) nên AD cũng đồng thời là đường cao, hay \(A{\rm{D}} \bot KC.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 3 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 3 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 3 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 6 - Chương 3 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 7 - Chương 3 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
