 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Ôn tập chương III : Quan hệ giữa các yếu tố trong tam g..
Ôn tập chương III : Quan hệ giữa các yếu tố trong tam g..
Bài 67 trang 87 SGK Toán 7 tập 2
Cho tam giác MNP với đường trung tuyến MR và trọng tâm Q.
Đề bài
Cho tam giác \(MNP\) với đường trung tuyến \(MR\) và trọng tâm \(Q.\)
a) Tính tỉ số các diện tích của hai tam giác \(MPQ\) và \(RPQ.\)
b) Tính tỉ số các diện tích của hai tam giác \(MNQ\) và \(RNQ.\)
Từ các kết quả trên, hãy chứng minh các tam giác \(QMN, QNP, QPM\) có cùng diện tích.
Gợi ý: Hai tam giác ở mỗi câu a, b, c có chung đường cao.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất trọng tâm của tam giác.
Lời giải chi tiết
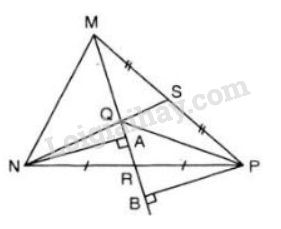
a) Vẽ \(PB \perp MR\) tại \(B\).
Vậy tam giác \(MPQ\) và \(RPQ\) có chung đường cao \(PB.\)
Vì \(Q\) là trọng tâm của \(∆MNP\) nên điểm \(Q\) thuộc đường trung tuyến \(MR\) và \(MQ = 2QR.\)
Ta có: \( S_{\Delta MPQ}= \dfrac{1}{2}MQ.PB\)\(\,= \dfrac{1}{2}. 2QR.PB =QR.PB \)
và \(S_{\Delta RPQ}= \dfrac{1}{2}QR.PB \)
Vậy: \(\dfrac{S_{\Delta MPQ}}{S_{\Delta RPQ}} = \dfrac{QR.PB}{\dfrac{1}{2}QR.PB} = 2 \) (1)
b) Vẽ \(NA \perp MR\) tại \(A\)
Vậy tam giác \(MNQ\) và \(RNQ\) có chung đường cao \(NA.\)
Vì \(Q\) là trọng tâm của \(∆MNP\) nên điểm \(Q\) thuộc đường trung tuyến \(MR\) và \(MQ = 2QR.\)
Ta có: \( S_{\Delta MNQ}= \dfrac{1}{2}MQ.NA\)\(= \dfrac{1}{2}. 2QR.NA =QR.NA \)
và \(S_{\Delta RNQ}= \dfrac{1}{2}QR.NA \)
Vậy: \(\dfrac{S_{\Delta MNQ}}{S_{\Delta RNQ}} = \dfrac{QR.NA}{\dfrac{1}{2}QR.NA} = 2 \) (2)
c) Hai tam giác \(∆RPQ\) và \(∆RQN\) có chung đường cao kẻ từ \(Q\) và \(PR = RN\) nên \({S_{RPQ}} = {S_{RQN}}\)
Vì \({S_{RPQ}} + {S_{RQN}} = {S_{QNP}}\)
Nên \({S_{QNP}} = 2{S_{RPQ}} = 2{S_{RQN}}\) hay \(\dfrac{S_{\Delta QNP}}{S_{\Delta RPQ}} =2\) (3)
Từ (1), (2), (3) ta có: \({S_{MNQ}} ={S_{QNP}} ={S_{MPQ}}\)
(Chú ý: \(S\) là diện tích, ví dụ \({S_{MNQ}}\) là diện tích tam giác \(MNQ\)).
Loigiaihay.com













Danh sách bình luận