Đề kiểm tra 15 phút - Đề số 8 - Bài 2,3,4,5 - Chương 2 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 8 - Bài 2,3,4,5 - Chương 2 - Hình học 7
Đề bài
Cho \(\Delta ABC\) có AB = AC, tia phân giác của góc A cắt cạnh BC tại D. Lấy E trên AD. Chứng minh rằng:
a) \(\Delta AEB = \Delta AEC\)
b) ED là tia phân giác của góc \(\widehat {BEC}\)
c) \(AD \bot BC.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Tam giác bằng nhau
Tính chất góc ngoài của tam giác
Tính chất tia phân giác của 1 góc
Lời giải chi tiết
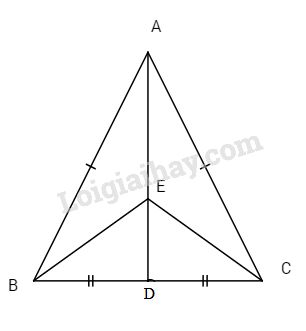
a) Xét \(\Delta AEB \) và \( \Delta AEC\) có:
+) AE là cạnh chung
+) \(\widehat {DAB} = \widehat {DAC}\)(giả thiết)
+) \(AB = AC\) (giả thiết)
Do đó \(\Delta AEB = \Delta AEC\) (c.g.c)
b) Ta có \(\widehat {BED}\) là góc ngoài của \(\Delta AEB \) nên \(\widehat {BED} = \widehat {BAE} + \widehat {EBA}\) (góc ngoài của tam giác bằng tổng hai góc trong không kề)
Tương tự \(\widehat {CED} = \widehat {CAE} + \widehat {ECA}\).
Mà \(\widehat {BAE} = \widehat {CAE}\) và \(\widehat {EBA} = \widehat {ECA}\) (do \(\Delta AEB = \Delta AEC\))
\( \Rightarrow \widehat {BED} = \widehat {CED}\), chứng tỏ ED là tia phân giác của góc \(\widehat {BEC}\).
c) Xét \(\Delta ADB\) và \(\Delta ADC\) có:
+) AD chung,
+) \(\widehat {BAD} = \widehat {CAD}\) (giả thiết),
+) AB = AC (giả thiết).
Vậy \(\Delta ADB=\Delta ADC\) (c.g.c)
\( \Rightarrow \widehat {ADB} = \widehat {ADC}\) (góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC} = {180^o}\) (kề bù) \( \Rightarrow \widehat {ADB} = \widehat {ADC} = {90^o}\).
Chứng tỏ \(AD \bot BC.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 9 - Bài 2,3,4,5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 10 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 11 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 13 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 14 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
