Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
Đề bài
Hàm số $y = - x^{3} + 3x^{2} + 2$ đồng biến trên khoảng nào trong các khoảng sau?
-
A.
$\left( {- \infty;0} \right)$.
-
B.
$\left( {2; + \infty} \right)$.
-
C.
$\left( {- 1;1} \right)$.
-
D.
$\left( {0;2} \right)$.
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [-1; 1]. Biết f(-1) = 1, f(1) = -1. Giá trị của tích phân $\int\limits_{- 1}^{1}{f'(x)dx}$ bằng
-
A.
0.
-
B.
2.
-
C.
−2.
-
D.
1.
-
A.
$\overset{\rightarrow}{SA} + \overset{\rightarrow}{SB} = \overset{\rightarrow}{SC} + \overset{\rightarrow}{SD}$.
-
B.
$\overset{\rightarrow}{AB} + \overset{\rightarrow}{AD} = \overset{\rightarrow}{AC}$.
-
C.
$\overset{\rightarrow}{AB} - \overset{\rightarrow}{AD} = \overset{\rightarrow}{DB}$.
-
D.
$\overset{\rightarrow}{SA} + \overset{\rightarrow}{SC} = \overset{\rightarrow}{SB} + \overset{\rightarrow}{SD}$.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2; 2; 3), B(0; -4; 1). Tọa độ trung điểm của đoạn thẳng AB là
-
A.
$\left( {- 1; - 3; - 1} \right)$.
-
B.
$\left( {1; - 1;2} \right)$.
-
C.
$\left( {2; - 2;4} \right)$.
-
D.
$\left( {- 2; - 6; - 2} \right)$.
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overset{\rightarrow}{a}\left( {1;2;3} \right)$, $\overset{\rightarrow}{b}\left( {0; - 1;1} \right)$. Độ dài của vectơ $2\overset{\rightarrow}{a} - \overset{\rightarrow}{b}$ bằng
-
A.
54.
-
B.
$\sqrt{54}$.
-
C.
62.
-
D.
$\sqrt{62}$.
Cho cấp số cộng $\left( u_{n} \right)$ có $u_{1} = 1$, $u_{2} = - 2$. Số hạng thứ 5 của cấp số cộng là
-
A.
−9.
-
B.
−7.
-
C.
−14.
-
D.
−11.
Cho hàm số y = f(x) liên tục trên [-2; 2]. Biết F(x) là một nguyên hàm của f(x) và F(2) – F(-2) = 5. Giá trị của tích phân $\int\limits_{- 2}^{2}{\left\lbrack {f(x) - 2x + 1} \right\rbrack dx}$ bằng
-
A.
7.
-
B.
9.
-
C.
1.
-
D.
−1.
-
A.
$y = \dfrac{x^{2} - 2x}{x - 1}$.
-
B.
$y = \dfrac{x^{2} + 2x}{x - 1}$.
-
C.
$y = \dfrac{- x^{2} + 2x}{x - 1}$.
-
D.
$y = \dfrac{x + 2}{x - 1}$.
Nguyên hàm của hàm số $f(x) = 2^{x}$ là
-
A.
$2^{x} + C$.
-
B.
$\dfrac{2^{x + 1}}{x + 1} + C$.
-
C.
$2^{x}.\ln 2 + C$.
-
D.
$\dfrac{2^{x}}{\ln 2} + C$.
Phương trình đường tiệm cận ngang của đồ thị hàm số $y = \dfrac{- x + 2}{x - 1}$ là
-
A.
y = -1.
-
B.
x = 1.
-
C.
y = 1.
-
D.
x = -1.
Cho hình chóp tứ giác S. ABCD có SA vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB với mặt phẳng (ABCD) là
-
A.
$\widehat{SAB}$.
-
B.
$\widehat{ASB}$.
-
C.
$\widehat{DBA}$.
-
D.
$\widehat{SBA}$.
Nghiệm của phương trình $\sin\left( {x + \dfrac{\pi}{3}} \right) = - \dfrac{1}{2}$ là
-
A.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{2} + k\pi} \\ {x = \dfrac{5\pi}{6} + k\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
-
B.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{6} + k2\pi} \\ {x = \dfrac{\pi}{2} + k2\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
-
C.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{2} + k2\pi} \\ {x = \dfrac{5\pi}{6} + k2\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
-
D.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{6} + k\pi} \\ {x = \dfrac{\pi}{2} + k\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
Cho hàm số $f(x) = \log_{3}\left( {2x - 3} \right)$.
a) Tập xác định của hàm số là $\left\lbrack {\dfrac{3}{2}; + \infty} \right)$.
b) $f'(x) = \dfrac{2}{\left( {2x - 3} \right)\ln 3}$, $\forall x \in \left( {\dfrac{3}{2}; + \infty} \right)$.
c) Phương trình $f(x) = \log_{3}\left( {x^{2} - x - 1} \right)$ có hai nghiệm phân biệt.
d) Gọi S là tập hợp tất cả các nghiệm nguyên của bất phương trình $f(x) \leq 4$. Tổng tất cả các phần tử của S bằng 903.
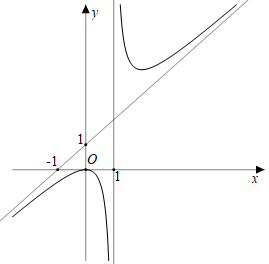
Cho hàm số $y = \dfrac{ax^{2} + bx + c}{x + d}$ có đồ thị như hình vẽ dưới đây. Biết rằng điểm O(0; 0) là điểm cực đại của đồ thị hàm số.
a) Phương trình đường tiệm cận xiên của đồ thị hàm số là y = x + 1.
b) Điểm cực tiểu của đồ thị hàm số là T(2; 4).
c) Hàm số đồng biến trên $\left( {1; + \infty} \right)$.
d) Gọi A, B là hai điểm di động trên đồ thị hàm số sao cho các tiếp tuyến của đồ thị hàm số tại A và B luôn song song với nhau. Khi khoảng cách từ điểm M(4; 1) đến đường thẳng AB lớn nhất thì độ dài đoạn thẳng AB bằng $2\sqrt{5}$.
Cho hình lăng trụ $ABC.A'B'C'$ có tất cả các cạnh bằng a, $\widehat{A^{\prime}AB} = 120^{\text{o}}$, $\widehat{A^{\prime}AC} = 60^{\text{o}}$. Gọi M là trung điểm của BC, N là điểm thỏa mãn $\overset{\rightarrow}{BN} = \dfrac{2}{3}\overset{\rightarrow}{BB^{\prime}}$.

a) Giả sử $\overset{\rightarrow}{A^{\prime}M} = x.\overset{\rightarrow}{AB} + y.\overset{\rightarrow}{AC} + z.\overset{\rightarrow}{AA^{\prime}}$ thì $x + y = z$.
b) $\overset{\rightarrow}{NB} = - 2\overset{\rightarrow}{NB^{\prime}}$.
c) $\overset{\rightarrow}{AB} + \overset{\rightarrow}{CC^{\prime}} = \overset{\rightarrow}{AB^{\prime}}$.
d) $\overset{\rightarrow}{A^{\prime}M}.\overset{\rightarrow}{C^{\prime}N} = \dfrac{4a^{2}}{3}$.
Một vật đang đứng yên thì bắt đầu chuyển động nhanh dần đều trong khoảng 10 giây với gia tốc là a $\left( \text{m/s}^{\text{2}} \right)$, a > 0. Biết rằng quãng đường vật đi được sau 5 giây kể từ khi bắt đầu chuyển động là 25 m.
a) Vận tốc của vật tại thời điểm t = 5 (s) là 10 (m/s).
b) Vận tốc tức thời của vật là v(t) = at (m/s).
c) a = 2.
d) Quãng đường vật đi được sau 10 giây kể từ khi bắt đầu chuyển động là 50 m.
Một người dùng ba loại nguyên liệu A, B, C để sản xuất ra hai loại sản phẩm P và Q. Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1 kg sản phẩm mỗi loại được cho trong bảng sau:

Biết 1 kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Người đó đã lập được phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Hỏi lãi cao nhất bằng bao nhiêu triệu đồng?
Gọi S là tập hợp tất cả các giá trị của a thuộc \(\left[ {\pi ;10\pi } \right]\) sao cho \(\int\limits_0^a {\cos xdx} = \frac{1}{2}\). Số phần tử của S là bao nhiêu?
Cho tứ diện ABCD có AB = 4, \(AC = AD = CD = 2\sqrt 3 \), \(BC = BD = \sqrt 7 \). Tính khoảng cách giữa hai đường thẳng AB và CD (làm tròn kết quả đến hàng phần trăm).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1. Gọi T là tập hợp tất cả các điểm M(x; y), trong đó \(x,y \in \mathbb{Z}\), sao cho từ M kẻ được 2 tiếp tuyến MA, MB đến (C) (A, B là các tiếp điểm) thỏa mãn \(\widehat {AMB} \ge {60^{\rm{o}}}\). Chọn ngẫu nhiên 2 điểm trong T. Biết xác suất để đường thẳng đi qua 2 điểm được chọn song song với trục Ox bằng \(\frac{1}{a}\). Tính \({a^2}\).
Một bể bơi hình bán nguyệt có đường kính là AB = 100 m. Một người muốn bơi từ vị trí A đến vị trí C theo phương thẳng rồi lên bờ đi bộ từ C đến B. Biết rằng vận tốc bơi là 5 km/h và vận tốc đi bộ là 6 km/h. Hỏi thời gian tối đa để người đó hoàn thành lộ trình như trên là bao nhiêu phút? (Làm tròn kết quả đến hàng phần trăm).

Một cái lều có dạng hình chóp tứ giác đều, cạnh đáy bằng 8 m và chiều cao là 3 m. Cửa vào lều là hình thang EFGH trong đó AE = FB và EF = 4 m. Gọi G, H lần lượt là trung điểm của SF và SE. Một nguồn sáng đặt cách đỉnh S 1 m ở phía dưới. Ánh sáng chiếu ra ngoài qua cửa tạo thành một vùng được chiếu sáng EFG’H’. Diện tích vùng được chiếu sáng là bao nhiêu (Làm tròn kết quả đến hàng đơn vị)?

Lời giải và đáp án
Hàm số $y = - x^{3} + 3x^{2} + 2$ đồng biến trên khoảng nào trong các khoảng sau?
-
A.
$\left( {- \infty;0} \right)$.
-
B.
$\left( {2; + \infty} \right)$.
-
C.
$\left( {- 1;1} \right)$.
-
D.
$\left( {0;2} \right)$.
Đáp án : D
Tính đạo hàm và lập xét dấu của hàm số.
\(y' = - 3{x^2} + 6x\); \(y' = 0 \Leftrightarrow - 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
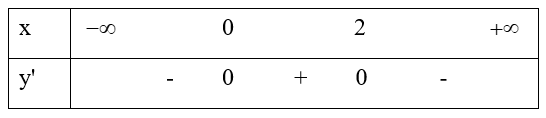
Từ bảng biến thiên, suy ra hàm số đồng biến trên (0; 2).
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [-1; 1]. Biết f(-1) = 1, f(1) = -1. Giá trị của tích phân $\int\limits_{- 1}^{1}{f'(x)dx}$ bằng
-
A.
0.
-
B.
2.
-
C.
−2.
-
D.
1.
Đáp án : C
Áp dụng định nghĩa tích phân: Cho hàm số f(x) liên tục trên đoạn [a;b]. Nếu F(x) là một nguyên hàm của f(x) trên đoạn [a;b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x). \(\int_a^b f (x){\mkern 1mu} dx = F(x)|_a^b = F(b) - F(a)\).
\(\int\limits_{ - 1}^1 {f'\left( x \right)dx} = f(x)\left| {\begin{array}{*{20}{c}}{^1}\\{_{ - 1}}\end{array}} \right. = f(1) - f( - 1) = - 1 - 1 = - 2\).
-
A.
$\overset{\rightarrow}{SA} + \overset{\rightarrow}{SB} = \overset{\rightarrow}{SC} + \overset{\rightarrow}{SD}$.
-
B.
$\overset{\rightarrow}{AB} + \overset{\rightarrow}{AD} = \overset{\rightarrow}{AC}$.
-
C.
$\overset{\rightarrow}{AB} - \overset{\rightarrow}{AD} = \overset{\rightarrow}{DB}$.
-
D.
$\overset{\rightarrow}{SA} + \overset{\rightarrow}{SC} = \overset{\rightarrow}{SB} + \overset{\rightarrow}{SD}$.
Đáp án : A
Áp dụng quy tắc trung điểm, quy tắc ba điểm, quy tắc hình bình hành để giải.
Gọi I, J lần lượt là trung điểm của AB và CD.
Theo quy tắc trung điểm: \(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SI} \), \(\overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SJ} \).
Mà \(\overrightarrow {SI} \ne \overrightarrow {SJ} \Rightarrow \overrightarrow {SA} + \overrightarrow {SB} \ne \overrightarrow {SC} + \overrightarrow {SD} \). Vậy đẳng thức ở đáp án A sai.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2; 2; 3), B(0; -4; 1). Tọa độ trung điểm của đoạn thẳng AB là
-
A.
$\left( {- 1; - 3; - 1} \right)$.
-
B.
$\left( {1; - 1;2} \right)$.
-
C.
$\left( {2; - 2;4} \right)$.
-
D.
$\left( {- 2; - 6; - 2} \right)$.
Đáp án : B
Toạ độ trung điểm I của đoạn thẳng AB là \(I\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\).
\(I\left( {\frac{{2 + 0}}{2};\frac{{2 - 4}}{2};\frac{{3 + 1}}{2}} \right) \Rightarrow I\left( {1; - 1;2} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overset{\rightarrow}{a}\left( {1;2;3} \right)$, $\overset{\rightarrow}{b}\left( {0; - 1;1} \right)$. Độ dài của vectơ $2\overset{\rightarrow}{a} - \overset{\rightarrow}{b}$ bằng
-
A.
54.
-
B.
$\sqrt{54}$.
-
C.
62.
-
D.
$\sqrt{62}$.
Đáp án : B
Vectơ \(\overrightarrow a\left( {{x_a};{y_a};{z_a}} \right)\) có độ dài là: \(\left| {\overrightarrow a} \right| = \sqrt {{x_a}^2 + {y_a}^2 + {z_a}^2} \).
\(2\overrightarrow a - \overrightarrow b = \left( {2.1 - 0;2.2 + 1;2.3 - 1} \right) = \left( {2;5;5} \right) \Rightarrow \left| {2\overrightarrow a - \overrightarrow b } \right| = \sqrt {{2^2} + {5^2} + {5^2}} = \sqrt {54} \).
Cho cấp số cộng $\left( u_{n} \right)$ có $u_{1} = 1$, $u_{2} = - 2$. Số hạng thứ 5 của cấp số cộng là
-
A.
−9.
-
B.
−7.
-
C.
−14.
-
D.
−11.
Đáp án : D
Áp dụng công thức số hạng tổng quát của cấp số cộng: \({u_n} = {u_1} + (n - 1)d\).
\(d = {u_2} - {u_1} = - 2 - 1 = - 3\).
\({u_5} = 1 + (5 - 1).( - 3) = - 11\).
Cho hàm số y = f(x) liên tục trên [-2; 2]. Biết F(x) là một nguyên hàm của f(x) và F(2) – F(-2) = 5. Giá trị của tích phân $\int\limits_{- 2}^{2}{\left\lbrack {f(x) - 2x + 1} \right\rbrack dx}$ bằng
-
A.
7.
-
B.
9.
-
C.
1.
-
D.
−1.
Đáp án : B
Áp dụng định nghĩa tích phân và công thức tính tích phân của hàm số lũy thừa.
\(\int\limits_{ - 2}^2 {\left[ {f\left( x \right) - 2x + 1} \right]dx} = \int\limits_{ - 2}^2 {f(x)dx} + \int\limits_{ - 2}^2 {( - 2x + 1)dx} \)
\( = F(2) - F( - 2) + 4 = 5 + 4 = 9\).
-
A.
$y = \dfrac{x^{2} - 2x}{x - 1}$.
-
B.
$y = \dfrac{x^{2} + 2x}{x - 1}$.
-
C.
$y = \dfrac{- x^{2} + 2x}{x - 1}$.
-
D.
$y = \dfrac{x + 2}{x - 1}$.
Đáp án : A
Dựa vào hình dạng đồ thị, các điểm đồ thị đi qua và tính đơn điệu để tìm công thức hàm số.
Loại đáp án D vì hình dạng đồ thị trong hình không phải là của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) \((c \ne 0)\).
Đồ thị đi qua điểm (2; 0) nên loại đáp án B.
Xét \(y = \frac{{{x^2} - 2x}}{{x - 1}} \Rightarrow y' = \frac{{(2x - 2)(x - 1) - ({x^2} - 2x)}}{{{{(x - 1)}^2}}} = \frac{{{x^2} - 2x + 2}}{{{{(x - 1)}^2}}} > 0\), \(\forall x \ne 1\).
Xét \(y = \frac{{ - {x^2} + 2x}}{{x - 1}} \Rightarrow y' = \frac{{( - 2x + 2)(x - 1) - ( - {x^2} + 2x)}}{{{{(x - 1)}^2}}} = \frac{{ - {x^2} + 2x - 2}}{{{{(x - 1)}^2}}} < 0\), \(\forall x \ne 1\).
Đồ thị trong hình đồng biến từng khoảng xác định nên hàm số cần tìm là \(y = \frac{{{x^2} - 2x}}{{x - 1}}\).
Nguyên hàm của hàm số $f(x) = 2^{x}$ là
-
A.
$2^{x} + C$.
-
B.
$\dfrac{2^{x + 1}}{x + 1} + C$.
-
C.
$2^{x}.\ln 2 + C$.
-
D.
$\dfrac{2^{x}}{\ln 2} + C$.
Đáp án : D
Áp dụng công thức nguyên hàm của hàm số mũ: \(\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\).
\(\int {f\left( x \right)dx} = \int {{2^x}dx} = \frac{{{2^x}}}{{\ln 2}} + C\).
Phương trình đường tiệm cận ngang của đồ thị hàm số $y = \dfrac{- x + 2}{x - 1}$ là
-
A.
y = -1.
-
B.
x = 1.
-
C.
y = 1.
-
D.
x = -1.
Đáp án : A
Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\) \((c \ne 0)\) là \(y = \frac{a}{c}\).
Phương trình đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{ - x + 2}}{{x - 1}}\) là \(y = - 1\).
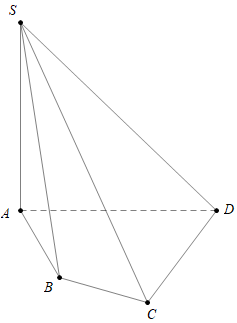
Cho hình chóp tứ giác S. ABCD có SA vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB với mặt phẳng (ABCD) là

-
A.
$\widehat{SAB}$.
-
B.
$\widehat{ASB}$.
-
C.
$\widehat{DBA}$.
-
D.
$\widehat{SBA}$.
Đáp án : D
Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d’ của đường thẳng d trên (P).
A là hình chiếu của S trên mặt phẳng (ABCD), do đó AB là hình chiếu của SB trên mặt phẳng (ABCD).
Khi đó \(\left( {SB,(ABCD)} \right) = \left( {SB,AB} \right) = \widehat {SBA}\).
Nghiệm của phương trình $\sin\left( {x + \dfrac{\pi}{3}} \right) = - \dfrac{1}{2}$ là
-
A.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{2} + k\pi} \\ {x = \dfrac{5\pi}{6} + k\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
-
B.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{6} + k2\pi} \\ {x = \dfrac{\pi}{2} + k2\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
-
C.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{2} + k2\pi} \\ {x = \dfrac{5\pi}{6} + k2\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
-
D.
$\left\lbrack \begin{array}{l} {x = - \dfrac{\pi}{6} + k\pi} \\ {x = \dfrac{\pi}{2} + k\pi} \end{array} \right.,\, k \in {\mathbb{Z}}$.
Đáp án : C
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\), \(k \in \mathbb{Z}\).
\(\sin \left( {x + \frac{\pi }{3}} \right) = \sin \left( { - \frac{\pi }{6}} \right) \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{3} = - \frac{\pi }{6} + k2\pi \\x + \frac{\pi }{3} = \pi - \left( { - \frac{\pi }{6}} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{2} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\), \(k \in \mathbb{Z}\).
Cho hàm số $f(x) = \log_{3}\left( {2x - 3} \right)$.
a) Tập xác định của hàm số là $\left\lbrack {\dfrac{3}{2}; + \infty} \right)$.
b) $f'(x) = \dfrac{2}{\left( {2x - 3} \right)\ln 3}$, $\forall x \in \left( {\dfrac{3}{2}; + \infty} \right)$.
c) Phương trình $f(x) = \log_{3}\left( {x^{2} - x - 1} \right)$ có hai nghiệm phân biệt.
d) Gọi S là tập hợp tất cả các nghiệm nguyên của bất phương trình $f(x) \leq 4$. Tổng tất cả các phần tử của S bằng 903.
a) Tập xác định của hàm số là $\left\lbrack {\dfrac{3}{2}; + \infty} \right)$.
b) $f'(x) = \dfrac{2}{\left( {2x - 3} \right)\ln 3}$, $\forall x \in \left( {\dfrac{3}{2}; + \infty} \right)$.
c) Phương trình $f(x) = \log_{3}\left( {x^{2} - x - 1} \right)$ có hai nghiệm phân biệt.
d) Gọi S là tập hợp tất cả các nghiệm nguyên của bất phương trình $f(x) \leq 4$. Tổng tất cả các phần tử của S bằng 903.
a) ĐKXĐ của hàm số logarit \(y = {\log _a}f(x)\): \(f(x) > 0\).
b) Công thức đạo hàm của hàm số logarit: \(\left[ {{{\log }_a}f(x)} \right]' = \frac{{f'(x)}}{{f(x)\ln a}}\).
c) Giải phương trình \(f\left( x \right) = {\log _3}\left( {{x^2} - x - 1} \right)\), đối chiếu với ĐKXĐ rồi kết luận nghiệm.
d) Giải bất phương trình \(f\left( x \right) \le 4\), tìm các phần tử thuộc S rồi áp dụng công thức \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2}\) để tính tổng.
a) Sai. ĐKXĐ: \(2x - 3 > 0 \Leftrightarrow x > \frac{3}{2}\). Vậy tập xác định của hàm số là \(\left( {\frac{3}{2}; + \infty } \right)\).
b) Đúng. \(f'\left( x \right) = \frac{{(2x - 3)'}}{{(2x - 3)\ln 3}} = \frac{2}{{\left( {2x - 3} \right)\ln 3}}\), \(\forall x \in \left( {\frac{3}{2}; + \infty } \right)\).
c) Sai. \(f(x) = {\log _3}\left( {{x^2} - x - 1} \right) \Leftrightarrow {\log _3}\left( {2x - 3} \right) = {\log _3}\left( {{x^2} - x - 1} \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}2x - 3 = {x^2} - x - 1\\x > \frac{{1 + \sqrt 5 }}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 3x + 2 = 0\\x > \frac{{1 + \sqrt 5 }}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\\x > \frac{{1 + \sqrt 5 }}{2}\end{array} \right. \Leftrightarrow x = 2\).
Vậy phương trình có duy nhất một nghiệm.
d) Sai. \(f\left( x \right) \le 4 \Leftrightarrow {\log _3}\left( {2x - 3} \right) \le 4 \Leftrightarrow \left\{ \begin{array}{l}x > \frac{3}{2}\\2x - 3 \le {3^4}\end{array} \right. \Leftrightarrow \frac{3}{2} < x \le 42\).
Do đó S = {2; 3; …; 42}, gồm \(\frac{{42 - 2}}{1} + 1 = 41\) phần tử.
Tổng các phần tử của S là: \(2 + 3 + ... + 42 = \frac{{(2 + 42)}}{2}.41 = 902\).
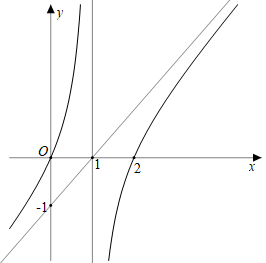
Cho hàm số $y = \dfrac{ax^{2} + bx + c}{x + d}$ có đồ thị như hình vẽ dưới đây. Biết rằng điểm O(0; 0) là điểm cực đại của đồ thị hàm số.

a) Phương trình đường tiệm cận xiên của đồ thị hàm số là y = x + 1.
b) Điểm cực tiểu của đồ thị hàm số là T(2; 4).
c) Hàm số đồng biến trên $\left( {1; + \infty} \right)$.
d) Gọi A, B là hai điểm di động trên đồ thị hàm số sao cho các tiếp tuyến của đồ thị hàm số tại A và B luôn song song với nhau. Khi khoảng cách từ điểm M(4; 1) đến đường thẳng AB lớn nhất thì độ dài đoạn thẳng AB bằng $2\sqrt{5}$.
a) Phương trình đường tiệm cận xiên của đồ thị hàm số là y = x + 1.
b) Điểm cực tiểu của đồ thị hàm số là T(2; 4).
c) Hàm số đồng biến trên $\left( {1; + \infty} \right)$.
d) Gọi A, B là hai điểm di động trên đồ thị hàm số sao cho các tiếp tuyến của đồ thị hàm số tại A và B luôn song song với nhau. Khi khoảng cách từ điểm M(4; 1) đến đường thẳng AB lớn nhất thì độ dài đoạn thẳng AB bằng $2\sqrt{5}$.
a) Từ các điểm thuộc tiệm cận xiên, lập hệ phương trình để tìm phương trình đường tiệm cận xiên.
b) Tìm tâm đối xứng của đồ thị, từ đó suy ra tọa độ của điểm cực tiểu.
c) Quan sát hướng đi của đồ thị để suy ra tính đơn điệu.
d) Xác định hệ số a, b, c, d của hàm số. Gọi I là trung điểm của AB và chứng minh I cố định, suy ra \(\max \left[ {d\left( {M,AB} \right)} \right] = MI\) khi \(MI \bot AB\). Lập phương trình đường thẳng AB, tìm tọa độ AB và tính độ dài AB.
a) Đúng. Giả sử tiệm cận xiện của đồ thị có phương trình \(y = mx + n\). Tiệm cận xiên đó đi qua các điểm có tọa độ (-1; 0) và (0; 1) nên ta có \(\left\{ \begin{array}{l}0 = - 1m + n\\1 = 0m + n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\n = 1\end{array} \right. \Rightarrow y = x + 1\).
b) Đúng. Tâm đối xứng của đồ thị là giao điểm của tiệm cận xiên y = x + 1 và tiệm cận đứng x = 1. Do đó, tâm đối xứng là điểm I(1; 2).
Vì tâm đối xứng của đồ thị cách đều hai cực trị nên điểm cực tiểu có tọa độ: \(\left\{ \begin{array}{l}2.1 - 0 = 2\\2.2 - 0 = 4\end{array} \right.\).
Vậy điểm cực tiểu của đồ thị hàm số là \(T\left( {2;4} \right)\).
c) Sai. Quan sát trên \(\left( {1; + \infty } \right)\), đồ thị có đi xuống từ trái sang phải nên hàm số không đồng biến trên \(\left( {1; + \infty } \right)\).
d) Đúng. Ta có hàm số của đồ thị trên là \(y = \frac{{a{x^2} + bx + c}}{{x - 1}}\).
Đồ thị đi qua O(0; 0) nên ta có \(0 = \frac{{a{{.0}^2} + b.0 + c}}{{0 - 1}} \Rightarrow c = 0\).
Có \(y = \frac{{a{x^2} + bx}}{{x - 1}} = ax + a + b + \frac{{a + b}}{{x - 1}}\), mà tiệm cận xiên của đồ thị là y = x + 1 nên \(\left\{ \begin{array}{l}a = 1\\a + b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\).
Vậy hàm số có đồ thị trên là \(y = \frac{{{x^2}}}{{x - 1}}\), đạo hàm \(y' = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}}\).
Gọi I là trung điểm của AB. Vì các tiếp tuyến tại A, B song song với nhau nên \(y{'_{{x_A}}} = y{'_{{x_B}}}\)
\( \Leftrightarrow \frac{{{x_A}^2 - 2{x_A}}}{{{{({x_A} - 1)}^2}}} = \frac{{{x_B}^2 - 2{x_B}}}{{{{({x_B} - 1)}^2}}} \Leftrightarrow \frac{{{x_A}^2 - 2{x_A} + 1 - 1}}{{{{({x_A} - 1)}^2}}} = \frac{{{x_B}^2 - 2{x_B} + 1 - 1}}{{{{({x_B} - 1)}^2}}}\)
\( \Leftrightarrow 1 - \frac{1}{{{{({x_A} - 1)}^2}}} = 1 - \frac{1}{{{{({x_B} - 1)}^2}}} \Leftrightarrow {({x_A} - 1)^2} = {({x_B} - 1)^2} \Leftrightarrow {x_A} - 1 = \pm ({x_B} - 1)\).
Loại \({x_A} - 1 = {x_B} - 1\) vì khi đó A trùng B. Suy ra \({x_A} - 1 = 1 - {x_B} \Leftrightarrow {x_A} + {x_B} = 2 \Leftrightarrow {x_I} = 1\).
Xét \({y_A} + {y_B} = \frac{{{x_A}^2}}{{{x_A} - 1}} + \frac{{{{(2 - {x_A})}^2}}}{{(2 - {x_A}) - 1}} = \frac{{{x_A}^2 - {{(2 - {x_A})}^2}}}{{{x_A} - 1}} = \frac{{4{x_A} - 4}}{{{x_A} - 1}} = 4 \Leftrightarrow {y_I} = 2\).
Vậy trung điểm I(1; 2) của đoạn thẳng AB là một điểm cố định.
Gọi H là hình chiếu của M trên AB. Khi đó \(d\left( {M,AB} \right) = MH \le MI\). Dấu “=” xảy ra khi \(MI \bot AB\).
Đường thẳng AB qua I(1; 2), nhận \(\overrightarrow {IM} = (3; - 1)\) làm vecto pháp tuyến nên có phương trình:
\(3(x - 1) - 1(y - 2) = 0 \Leftrightarrow 3x - y - 1 = 0 \Leftrightarrow y = 3x - 1\).
Phương trình hoành độ giao điểm của đồ thị \(y = \frac{{{x^2}}}{{x - 1}}\) và đường thẳng AB là:
\(\frac{{{x^2}}}{{x - 1}} = 3x - 1 \Leftrightarrow 2{x^2} - 4x + 1 = 0 \Leftrightarrow \frac{{2 \pm \sqrt 2 }}{2}\).
Suy ra \(A\left( {\frac{{2 + \sqrt 2 }}{2};\frac{{4 + 3\sqrt 2 }}{2}} \right)\) và \(B\left( {\frac{{2 - \sqrt 2 }}{2};\frac{{4 - 3\sqrt 2 }}{2}} \right)\).
\(AB = \sqrt {{{\left( {\frac{{2 - \sqrt 2 }}{2} - \frac{{2 + \sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{4 - 3\sqrt 2 }}{2} - \frac{{4 + 3\sqrt 2 }}{2}} \right)}^2}} = 2\sqrt 5 \).
Cho hình lăng trụ $ABC.A'B'C'$ có tất cả các cạnh bằng a, $\widehat{A^{\prime}AB} = 120^{\text{o}}$, $\widehat{A^{\prime}AC} = 60^{\text{o}}$. Gọi M là trung điểm của BC, N là điểm thỏa mãn $\overset{\rightarrow}{BN} = \dfrac{2}{3}\overset{\rightarrow}{BB^{\prime}}$.

a) Giả sử $\overset{\rightarrow}{A^{\prime}M} = x.\overset{\rightarrow}{AB} + y.\overset{\rightarrow}{AC} + z.\overset{\rightarrow}{AA^{\prime}}$ thì $x + y = z$.
b) $\overset{\rightarrow}{NB} = - 2\overset{\rightarrow}{NB^{\prime}}$.
c) $\overset{\rightarrow}{AB} + \overset{\rightarrow}{CC^{\prime}} = \overset{\rightarrow}{AB^{\prime}}$.
d) $\overset{\rightarrow}{A^{\prime}M}.\overset{\rightarrow}{C^{\prime}N} = \dfrac{4a^{2}}{3}$.
a) Giả sử $\overset{\rightarrow}{A^{\prime}M} = x.\overset{\rightarrow}{AB} + y.\overset{\rightarrow}{AC} + z.\overset{\rightarrow}{AA^{\prime}}$ thì $x + y = z$.
b) $\overset{\rightarrow}{NB} = - 2\overset{\rightarrow}{NB^{\prime}}$.
c) $\overset{\rightarrow}{AB} + \overset{\rightarrow}{CC^{\prime}} = \overset{\rightarrow}{AB^{\prime}}$.
d) $\overset{\rightarrow}{A^{\prime}M}.\overset{\rightarrow}{C^{\prime}N} = \dfrac{4a^{2}}{3}$.
Áp dụng khái niệm hai vecto bằng nhau, hai vecto đối nhau, quy tắc ba điểm, quy tắc hình bình hành, góc giữa hai vecto, tích vô hướng của hai vecto.
a) Sai. \(\overrightarrow {A'M} = \overrightarrow {A'A} + \overrightarrow {AM} = - \overrightarrow {AA'} + \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} - \overrightarrow {AA'} \).
Vậy \(x + y = \frac{1}{2} + \frac{1}{2} = 1 = - ( - 1) = - z\).
b) Đúng. \(\overrightarrow {BN} = \frac{2}{3}\overrightarrow {BB'} \Rightarrow BN = \frac{2}{3}BB \Rightarrow NB = 2NB'\).
Mà \(\overrightarrow {NB} \) và \(\overrightarrow {NB'} \) ngược chiều nên \(\overrightarrow {NB} = - 2\overrightarrow {NB'} \).
c) Đúng. \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AB} + \overrightarrow {BB'} = \overrightarrow {AB'} \).
d) Đúng. \(\overrightarrow {C'N} = \overrightarrow {AN} - \overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {BN} - \overrightarrow {AA'} - \overrightarrow {AC} \)
\( = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AA'} - \overrightarrow {AA'} - \overrightarrow {AC} = \overrightarrow {AB} - \frac{1}{3}\overrightarrow {AA'} - \overrightarrow {AC} \).
\(\overrightarrow {A'M} .\overrightarrow {C'N} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} - \overrightarrow {AA'} } \right).\left( {\overrightarrow {AB} - \overrightarrow {AC} - \frac{1}{3}\overrightarrow {AA'} } \right)\)
\( = \frac{1}{2}A{B^2} + \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AA'} .\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{2}A{C^2} + \overrightarrow {AA'} .\overrightarrow {AC} - \frac{1}{6}\overrightarrow {AB} .\overrightarrow {AA'} - \frac{1}{6}\overrightarrow {AC} .\overrightarrow {AA'} + \frac{1}{3}AA{'^2}\)
\( = \frac{1}{2}{a^2} + \frac{1}{4}{a^2} + \frac{1}{2}{a^2} - \frac{1}{4}{a^2} - \frac{1}{2}{a^2} + \frac{1}{2}{a^2} + \frac{1}{{12}}{a^2} - \frac{1}{{12}}{a^2} + \frac{1}{3}{a^2} = \frac{4}{3}{a^2}\).
Một vật đang đứng yên thì bắt đầu chuyển động nhanh dần đều trong khoảng 10 giây với gia tốc là a $\left( \text{m/s}^{\text{2}} \right)$, a > 0. Biết rằng quãng đường vật đi được sau 5 giây kể từ khi bắt đầu chuyển động là 25 m.
a) Vận tốc của vật tại thời điểm t = 5 (s) là 10 (m/s).
b) Vận tốc tức thời của vật là v(t) = at (m/s).
c) a = 2.
d) Quãng đường vật đi được sau 10 giây kể từ khi bắt đầu chuyển động là 50 m.
a) Vận tốc của vật tại thời điểm t = 5 (s) là 10 (m/s).
b) Vận tốc tức thời của vật là v(t) = at (m/s).
c) a = 2.
d) Quãng đường vật đi được sau 10 giây kể từ khi bắt đầu chuyển động là 50 m.
Vận tốc của vật sau t giây: \(v(t) = at + b\) (m/s).
Quãng đường vật di chuyển được sau t giây: \(s(t) = \frac{1}{2}a{t^2} + bt + c\).
Từ giả thiết, tìm các hệ số a, b, c và thay t theo yêu cầu đề bài để tính toán.
Vận tốc của vật sau t giây: \(v(t) = at + b\) (m/s).
Quãng đường vật di chuyển được sau t giây: \(s(t) = \frac{1}{2}a{t^2} + bt + c\).
Vì ban đầu vật đứng yên nên \(\left\{ \begin{array}{l}v(0) = 0 \Leftrightarrow 0 = a.0 + b \Leftrightarrow b = 0 \Rightarrow v(t) = at\\s(0) = 0 \Leftrightarrow 0 = \frac{1}{2}a{.0^2} + b.0 + c \Rightarrow c = 0 \Rightarrow s(t) = \frac{1}{2}a{t^2}\end{array} \right.\).
Theo đề bài, \(s(5) = 25 \Leftrightarrow \frac{1}{2}.a{.5^2} = 25 \Leftrightarrow a = 2 \Rightarrow \left\{ \begin{array}{l}v(t) = 2t\\s(t) = {t^2}\end{array} \right.\).
a) Đúng. v(5) = 2.5 = 10 (m/s).
b) Đúng. v(t) = at (m/s).
c) Đúng. a = 2.
d) Sai. \(s(10) = {10^2} = 100\) (m).
Một người dùng ba loại nguyên liệu A, B, C để sản xuất ra hai loại sản phẩm P và Q. Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1 kg sản phẩm mỗi loại được cho trong bảng sau:

Biết 1 kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Người đó đã lập được phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Hỏi lãi cao nhất bằng bao nhiêu triệu đồng?
– Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm).
– Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
– Lập bất phương trình biểu thị mối quan hệ giữa các đại lượng, biểu thị điều kiện đề bài đưa ra trong một tình huống nào đó… Giá trị nhỏ nhất hay lớn nhất của biểu thức P(x; y) = ax + by (b ≠ 0) trên miền đa giác lồi (kể cả biên) đạt được tại một đỉnh nào đó của đa giác.
Gọi x là số kg sản phẩm P, y là số kg sản phẩm Q cần sản xuất. Ta có hệ:
\(\left\{ \begin{array}{l}2x + 2y \le 10\\2y \le 4\\2x + 4y \le 12\\x,y \ge 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x + y \le 5\\y \le 2\\x + 2y \le 6\\x,y \ge 0\end{array} \right.\)
Miền nghiệm của hệ là miền ngũ giác ABCDE như hình với A(0; 0), B(0; 2), C(2; 2), D(4; 1), E(5; 0).

Số tiền lãi là: L = 3x + 5y (triệu đồng).
Ta có: L(0; 0) = 3.0 + 5.0 = 0;
L(0; 2) = 3.0 + 5.2 = 10;
L(2; 2) = 3.2 + 5.2 = 16;
L(4; 1) = 3.4 + 5.1 = 17;
L(5; 0) = 3.5 + 5.0 = 15.
Vậy cần sản xuất 4 kg sản phẩm P và 1 kg sản phẩm Q để có lãi cao nhất là 17 triệu đồng.
Gọi S là tập hợp tất cả các giá trị của a thuộc \(\left[ {\pi ;10\pi } \right]\) sao cho \(\int\limits_0^a {\cos xdx} = \frac{1}{2}\). Số phần tử của S là bao nhiêu?
Áp dụng quy tắc tính tích phân của hàm số lượng giác và công thức nghiệm của phương trình lượng giác cơ bản. Tìm số giá trị của a thuộc \(\left[ {\pi ;10\pi } \right]\).
\(\int\limits_0^a {\cos xdx} = \frac{1}{2} \Leftrightarrow \sin x\left| {\begin{array}{*{20}{c}}{^a}\\{_0}\end{array} = \frac{1}{2} \Leftrightarrow \sin a - \sin 0 = \frac{1}{2} \Leftrightarrow \sin a = \frac{1}{2}} \right. \)
\(\Leftrightarrow \sin a = \sin \frac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l}a = \frac{\pi }{6} + k2\pi \\a = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
Vì \(a \in \left[ {\pi ;10\pi } \right]\) nên ta có:
TH1: \(\pi \le \frac{\pi }{6} + k2\pi \le 10\pi \Leftrightarrow \frac{5}{{12}} \le k \le \frac{{59}}{{12}} \Rightarrow \) Các giá trị k nguyên thỏa mãn là \(k \in \{ 1;2;3;4\} \), do đó có 4 giá trị a thỏa mãn.
TH2: \(\pi \le \frac{{5\pi }}{6} + k2\pi \le 10\pi \Leftrightarrow \frac{1}{{12}} \le k \le \frac{{55}}{{12}} \Rightarrow \) Các giá trị k nguyên thỏa mãn là \(k \in \{ 1;2;3;4\} \), do đó có 4 giá trị a thỏa mãn.
Vậy S có 8 phần tử.
Cho tứ diện ABCD có AB = 4, \(AC = AD = CD = 2\sqrt 3 \), \(BC = BD = \sqrt 7 \). Tính khoảng cách giữa hai đường thẳng AB và CD (làm tròn kết quả đến hàng phần trăm).
Tìm đoạn vuông góc chung của AB và CD và tính độ dài đoạn thẳng đó.

Gọi M là trung điểm của CD. Lấy điểm N thuộc AB sao cho \(MN \bot AB\).
Vì AC = AD nên tam giác ACD cân tại A. Khi đó \(AM \bot CD\) (1)
Vì BC = BD nên tam giác BCD cân tại B. Khi đó \(BM \bot CD\) (2)
Từ (1) và (2) suy ra \(CD \bot (ABM)\), mà \(MN \subset (ABM) \Rightarrow CD \bot MN\).
Như vậy MN là đoạn vuông góc chung của AB và CD, suy ra \(d\left( {AB,CD} \right) = MN\).
Vì \(AC = AD = CD = 2\sqrt 3 \) nên tam giác ACD đều, do đó \(AM = \frac{{\sqrt 3 }}{2}.2\sqrt 3 = 3\).
Xét tam giác BCM vuông tại M: \(BM = \sqrt {B{C^2} - C{M^2}} = \sqrt {7 - 3} = 2\) (định lí Pythagore).
Nửa chu vi tam giác AMB là \(p = \frac{{2 + 3 + 4}}{2} = 4,5\).
Diện tích tam giác AMB: \({S_{ABM}} = \sqrt {4,5.(4,5 - 2).(4,5 - 3).(4,5 - 4)} = \frac{{3\sqrt {15} }}{4}\).
Mặt khác \({S_{ABM}} = \frac{1}{2}.AB.MN \Leftrightarrow \frac{{3\sqrt {15} }}{4} = \frac{1}{2}.4.MN \Leftrightarrow MN = \frac{{3\sqrt {15} }}{8} \approx 1,45\).
Vậy \(d\left( {AB,CD} \right) = MN \approx 1,45\).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1. Gọi T là tập hợp tất cả các điểm M(x; y), trong đó \(x,y \in \mathbb{Z}\), sao cho từ M kẻ được 2 tiếp tuyến MA, MB đến (C) (A, B là các tiếp điểm) thỏa mãn \(\widehat {AMB} \ge {60^{\rm{o}}}\). Chọn ngẫu nhiên 2 điểm trong T. Biết xác suất để đường thẳng đi qua 2 điểm được chọn song song với trục Ox bằng \(\frac{1}{a}\). Tính \({a^2}\).
Dựa vào giả thiết tìm các điểm M thỏa mãn. Xét trong các điểm M đó tạo thành được bao nhiêu đường thẳng và bao nhiêu trong số đó song song với Ox. Áp dụng công thức xác suất cổ điển để tính.

Vì từ M(x; y) kẻ được 2 tiếp tuyến MA, MB đến (C) nên M nằm ngoài đường tròn (C).
Có \(\widehat {AMB} \ge {60^o} \Leftrightarrow \widehat {OMB} \ge {30^o} \Leftrightarrow \sin \widehat {OMB} \ge \sin {30^o} \Leftrightarrow \frac{{OB}}{{OM}} \ge \frac{1}{2} \Leftrightarrow OM \le 2OB = 2.1 = 2\).
Suy ra M có thể nằm trên hoặc bên trong đường tròn tâm O, bán kính bằng 2.
Mà x, y nguyên nên có 8 điểm M thỏa mãn với tọa độ:
(2; 0), (0; 2), (-2; 0), (0; -2), (1; 1), (-1; 1), (-1; -1), (1; -1).
Từ 8 điểm trên, ta kẻ được \(C_8^2 = 28\) đường thẳng, trong đó có 2 đường thẳng song song với trục Ox là y = 1 và y = -1.
Vậy xác suất để đường thẳng đi qua 2 điểm được chọn song song với Ox bằng \(\frac{2}{{28}} = \frac{1}{{14}} \Rightarrow {a^2} = {14^2} = 196\).
Một bể bơi hình bán nguyệt có đường kính là AB = 100 m. Một người muốn bơi từ vị trí A đến vị trí C theo phương thẳng rồi lên bờ đi bộ từ C đến B. Biết rằng vận tốc bơi là 5 km/h và vận tốc đi bộ là 6 km/h. Hỏi thời gian tối đa để người đó hoàn thành lộ trình như trên là bao nhiêu phút? (Làm tròn kết quả đến hàng phần trăm).

Tính độ dài đoạn thẳng AC và cung BC bằng các hệ thức lượng giác. Lập hàm số biểu diễn thời gian hoàn thành lộ trình. Tính đạo hàm và tìm giá trị lớn nhất của hàm số đó.
Đổi: 100 m = 0,1 km.
Giả sử \(\widehat {CAB} = \alpha \Rightarrow \widehat {COB} = 2\alpha \) và số đo cung BC bằng \(2\alpha \) (\(0 < \alpha < \frac{\pi }{2}\), đơn vị: rad).
Xét tam giác ACB vuông tại C, có: \(\cos \widehat {CAB} = \frac{{AC}}{{AB}}\).
\(\Rightarrow AC = AB\cos \widehat {CAB} = 0,1\cos \alpha \).
Độ dài cung BC là:
\({l_{BC}} = \frac{{AB}}{2}.2\alpha = 0,1\alpha \).
Thời gian người đó hoàn thành lộ trình là:
\(T(\alpha ) = \frac{{0,1\cos \alpha }}{5} + \frac{{0,1\alpha }}{6}\) (giờ).
\(T'(\alpha ) = \frac{{ - 0,1\sin \alpha }}{5} + \frac{{0,1}}{6} = 0 \Leftrightarrow \sin \alpha = \frac{5}{6} \Rightarrow \alpha = \arcsin \frac{5}{6}\).
Ta có \(T(0) = \frac{1}{{50}} = 0,02\), \(T\left( {\arcsin \frac{5}{6}} \right) \approx 0,027\), \(T\left( {\frac{\pi }{2}} \right) = \frac{\pi }{{120}} \approx 0,026\).
Vậy thời gian tối đa người đó hoàn thành lộ trình là \(T\left( {\arcsin \frac{5}{6}} \right).60 \approx 1,65\) (phút).
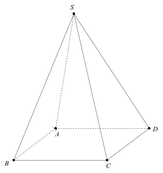
Một cái lều có dạng hình chóp tứ giác đều, cạnh đáy bằng 8 m và chiều cao là 3 m. Cửa vào lều là hình thang EFGH trong đó AE = FB và EF = 4 m. Gọi G, H lần lượt là trung điểm của SF và SE. Một nguồn sáng đặt cách đỉnh S 1 m ở phía dưới. Ánh sáng chiếu ra ngoài qua cửa tạo thành một vùng được chiếu sáng EFG’H’. Diện tích vùng được chiếu sáng là bao nhiêu (Làm tròn kết quả đến hàng đơn vị)?

Chọn hệ trục tọa độ ở vị trí phù hợp, tìm tọa độ các điểm E, F, G’, H’ rồi áp dụng công thức tính diện tích hình thang để tính diện tích vùng chiếu sáng.
Chọn hệ trục tọa độ Oxyz sao cho D trùng gốc tọa độ O, A thuộc tia Ox, C thuộc tia Oy, S có cao độ dương.
Khi đó D(0; 0; 0), A(8; 0; 0), B(8; 8; 0), C(0; 8; 0), S(4; 4; 3), I(4; 4; 2).
\(AE = FB = \frac{{AB - EF}}{2} = \frac{{8 - 4}}{2} = 2\), do đó E(8; 2; 0), F(8; 6; 0).
H là trung điểm của SE nên \(H\left( {6;3;\frac{3}{2}} \right)\), G là trung điểm của SF nên \(G\left( {6;5;\frac{3}{2}} \right)\).
Đường thẳng IH đi qua I, nhận \(\overrightarrow {IH} = \left( {2; - 1; - \frac{1}{2}} \right)\) làm vecto chỉ phương nên có phương trình tham số:
\(\left\{ \begin{array}{l}x = 4 + 2t\\y = 4 - t\\z = 2 - \frac{1}{2}t\end{array} \right.\) \((t \in \mathbb{R})\).
IH giao với mặt phẳng đáy tại \(0 = 2 - \frac{1}{2}t \Leftrightarrow t = 4\). Suy ra H’(12; 0; 0).
Đường thẳng IG đi qua I, nhận \(\overrightarrow {IG} = \left( {2;1; - \frac{1}{2}} \right)\) làm vecto chỉ phương nên có phương trình tham số:
\(\left\{ \begin{array}{l}x = 4 + 2t\\y = 4 + t\\z = 2 - \frac{1}{2}t\end{array} \right.\) \((t \in \mathbb{R})\).
IH giao với mặt phẳng đáy tại \(0 = 2 - \frac{1}{2}t \Leftrightarrow t = 4\). Suy ra G’(12; 8; 0).
Biểu diễn trên mặt phẳng (Oxy):

Diện tích hình thang EFG’H’ là: \({S_{EFG'H'}} = \frac{1}{2}(EF + G'H').d(EF,G'H') = \frac{1}{2}.(4 + 8).4 = 24\).
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2026 trường THPT Cửa Lò - Nghệ An
Đề KSCL Toán 12 lần 1 năm 2025 - 2026 trường THPT Triệu Sơn 3 - Thanh Hóa
Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng
Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình
Đề thi thử THPT môn Toán năm 2026 trường THPT Nguyễn Trung Thiên - Hà Tĩnh
Các bài khác cùng chuyên mục
- Đề thi thử THPT môn Toán năm 2026 trường THPT Nguyễn Trung Thiên - Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình
- Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
- Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
- Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng
- Đề thi thử THPT môn Toán năm 2026 trường THPT Nguyễn Trung Thiên - Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình
- Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
- Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
- Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng









Danh sách bình luận