Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình

Tải về

Đề khảo sát chất lượng Toán 12 năm 2025 - 2026 cụm 5 Ninh Bình

Đề bài

Xem đáp án

Làm đề thi

Tải về

Đề bài

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1 :

Dãy số nào sau đây là cấp số cộng?

A.

$\left( u_{n} \right):u_{n} = 2^{n} - 1$.
B.

$\left( u_{n} \right):u_{n} = 2u_{n - 1},\forall n \geq 2$.
C.

$\left( u_{n} \right):u_{n} = u_{n - 1} - 2,\forall n \geq 2$.
D.

$\left( u_{n} \right):u_{n} = \dfrac{1}{n}$.

Câu 2 :

Cho F(x) là nguyên hàm của hàm số $f(x) = 6x^{5} + \dfrac{1}{x^{3}}$ thỏa mãn F(1) = 0. Tîm F(x).

A.

$F(x) = x^{6} - \dfrac{1}{2x^{2}} + \dfrac{1}{2}$.
B.

$F(x) = x^{6} - \dfrac{1}{2x^{2}} - \dfrac{1}{2}$.
C.

$F(x) = x^{6} + \dfrac{1}{2x^{2}} - \dfrac{3}{2}$.
D.

$F(x) = x^{6} - \dfrac{3}{x^{2}} + 2$.

Câu 3 :

Biết ${\int{g(x)dx}} = G(x) + C$ (với C là hằng số). Khi đó khẳng định nào sau đây đúng?

A.

$g'(x) = G(x) + C$.
B.

$G'(x) = g(x) - C$.
C.

$g'(x) = G(x)$.
D.

$G'(x) = g(x)$.

Câu 4 :

Cho bảng phân bố tần số ghép lớp về độ dài của 60 lá dương xỉ trưởng thành như sau:

Tính khoảng tứ phân vị (làm tròn đến chữ số thập phân thứ nhất) của mẫu số liệu trên?

A.

13,7.
B.

13,6.
C.

13,5.
D.

13,8.

Câu 5 :

Cho hàm số y = f(x) có đạo hàm $f'(x) = (2x - 1)(x + 1)$. Hàm số y = f(x) có giá trị lớn nhất trên [-2; 0] bằng

A.

f(-2).
B.

$f\left( {- \dfrac{1}{2}} \right)$.
C.

f(0).
D.

f(-1).

Câu 6 :

Số đường tiệm cận của đồ thị hàm số $y = 2x + 3 + \dfrac{1}{x - 1}$ là

A.

3.
B.

0.
C.

1.
D.

2.

Câu 7 :

Cho ${{\log }_{0,2}}x>{{\log }_{0,2}}y$. Chọn khẳng định đúng:

A.

$x > y \geq 0$.
B.

$y > x \geq 0$.
C.

$x > y > 0$.
D.

$y > x > 0$.

Câu 8 :

Cho hình chóp đều S.ABCD có cạnh đáy 2a, cạnh bên 4a. Tính độ dài đường cao hình chóp.

A.

2a.
B.

$a\sqrt{14}$.
C.

3a.
D.

$a\sqrt{15}$.

Câu 9 :

Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm A(2; 1; -3), đồng thời vuông góc với hai mặt phẳng (Q): x + y + 3z = 0, (R): 2x – y + z = 0 là

A.

4x – 5y – 3z – 8 = 0.
B.

4x + 5y – 3z – 4 = 0.
C.

4x + 5y – 3z – 22 = 0.
D.

4x – 5y – 3z – 12 = 0.

Câu 10 :

Cho hình hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$. Khẳng định nào dưới đây sai?

A.

$\overset{\rightarrow}{AD} + \overset{\rightarrow}{BB_{1}} = \overset{\rightarrow}{AD_{1}}$.
B.

$\overset{\rightarrow}{AB} + \overset{\rightarrow}{AD} + \overset{\rightarrow}{AA_{1}} = \overset{\rightarrow}{AC_{1}}$.
C.

$\overset{\rightarrow}{AB} + \overset{\rightarrow}{DD_{1}} = \overset{\rightarrow}{AD_{1}}$.
D.

$\overset{\rightarrow}{AB} + \overset{\rightarrow}{CC_{1}} = \overset{\rightarrow}{AB_{1}}$.

Câu 11 :

Khoảng cách giữa hai điểm I(1; 4; -3) và K(6; 4; 5) là

A.

$\sqrt{89}$.
B.

$\sqrt{114}$.
C.

$\sqrt{103}$.
D.

$\sqrt{95}$.

Câu 12 :

Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án A, B, C, D. Hỏi đó là hàm số nào?

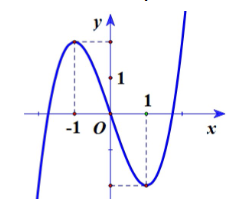
A graph of a function

Description automatically generated

A.

$y = - x^{3} + 3x$.
B.

$y = x^{3} + 2x + 1$.
C.

$y = x^{3} - 3x$.
D.

$y = x^{3} + 3x^{2}$.

Phần II: Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1 :

Một công ty sau khi ra mắt sản phẩm mới đã ghi nhận lợi nhuận P(t) (đơn vị: triệu đồng) sau t tháng kinh doanh. Trong năm đầu tiên, giả sử mối liên hệ giữa lợi nhuận và thời gian kinh doanh được mô hình hoá bởi hàm số: $P(t) = - t^{3} + 10t^{2} + 63t - 45$, $0 \leq t \leq 12$.

a) Hàm số biểu thị tốc độ tăng trưởng lợi nhuận $P'(t) = - 3t^{2} + 20t + 63t$.

Đúng

Sai

b) Lợi nhuận của công ty đạt mức tối đa tại thời điểm t = 9.

Đúng

Sai

c) Tại thời điểm t = 4 thì tốc độ tăng trưởng lợi nhuận là lớn nhất.

Đúng

Sai

d) Lợi nhuận của công ty sau 1 quý là 27 triệu đồng.

Đúng

Sai

Câu 2 :

Một công ty bất động sản thực hiện cuộc khảo sát khách hàng xem họ có nhu cầu mua ở mức giá nào cho một căn nhà, để tiến hành dự án xây dựng khu đô thị mới sắp tới. Kết quả khảo sát 500 khách hàng được ghi lại ở bảng sau:

a) Phương sai xấp xỉ 20,52.

Đúng

Sai

b) Biết rằng công ty sẽ xây dựng phân khúc nhà giá rẻ cho 25% số khách hàng có nhu cầu mua ở mức giá thấp nhất theo khảo sát, xây dựng phân khúc nhà giá cao cấp cho 25% số khách hàng có nhu cầu mua ở mức giá cao nhất theo khảo sát. Tuy nhiên trước hết sẽ ưu tiên xây dựng phân khúc nhà tầm trung hướng tới 50% số khách hàng còn lại. Khi đó theo khảo sát, độ chênh lệch giá cao nhất và giá thấp nhất (đúng đến hàng phần mười, đơn vị triệu đồng) dành cho phân khúc nhà tầm trung là 6,1 triệu.

Đúng

Sai

c) Tứ phân vị thứ ba là 25.

Đúng

Sai

d) Độ dài mỗi nhóm là 4.

Đúng

Sai

Câu 3 :

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c đều dương.

a) Mặt phẳng (ABC) đi qua điểm M(2; -2; 3) sao cho độ dài OA, OB, OC theo thứ tự lập thành cấp số cộng có công sai bằng 2. Khoảng cách từ điểm D(1; 1; 1) tới mặt phẳng (ABC) bằng $\dfrac{m}{n}$ với $\dfrac{m}{n}$ là phân số tối giản. Khi đó T = m + n = 8.

Đúng

Sai

b) Mặt phẳng (ABC) có phương trình $\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1$.

Đúng

Sai

c) Mặt phẳng (ABC) đi qua điểm H(1; 1; 1) sao cho H là trực tâm tam giác ABC là x + y + z – 3 = 0.

Đúng

Sai

d) Mặt phẳng (ABC) đi qua điểm G(1; 2; 3) sao cho G là trọng tâm tam giác ABC là 6x + 3y + 2z + 18 = 0.

Đúng

Sai

Câu 4 :

Cho một bể chứa nước và ban đầu chưa có nước. Người ta bắt đầu bơm nước vào bể với lưu lượng là $L_{1}(t) = 6t + 3$ (lít/phút). Cùng lúc đó, do bể có một vết nứt dưới đáy nên nước bị chảy ra ngoài với lưu lượng là $L_{2}(t) = 2t$ (lít/phút). Dung tích tối đa của bể là 2015 lít.

Hỏi trong các mệnh đề dưới đây, mệnh đề nào là đúng, mệnh đề nào là sai?

a) Nếu bơm được 30 phút thì dừng thì lượng nước trong bể chưa đầy bể.

Đúng

Sai

b) Thể tích nước được bơm vào bể trong 5 phút đầu tiên là 90 (lít).

Đúng

Sai

c) Thể tích nước chảy ra từ bể trong 5 phút đầu tiên là 10 (lít).

Đúng

Sai

d) Khi nước chảy vào vừa làm đầy bể, thì đã có nhiều hơn 900 lít nước bị chảy ra ngoài (làm tròn kết quả đến hàng đơn vị).

Đúng

Sai

Phần III: Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1 :

Một nhà máy A chuyên sản xuất một loại sản phẩm cho nhà máy B, nhà máy A chỉ bán sản phẩm cho nhà máy B và nhà máy B cam kết thu mua hết số sản phẩm mà nhà máy A sản xuất được. Nhà máy A có khả năng sản xuất được tối đa là 200 tấn sản phẩm trong 1 tháng. Nếu bán ra x tấn sản phẩm cho nhà máy B thì giá bán mỗi tấn sản phẩm là $50 - 0,0002{x^2}$ triệu đồng. Trong một tháng nhà máy A phải chi phí cho nhân công và chi cho khấu hao máy móc một lượng cố định là 150 triệu đồng, ngoài ra khi sản xuất mỗi tấn sản phẩm thì nhà máy phải chi phí thêm cho mua nguyên liệu là 35 triệu đồng. Biết rằng nhà máy A phải nộp 5% doanh thu cho cơ quan thuế. Tính lợi nhuận sau thuế (lợi nhuận sau khi đã trừ tiền thuế) lớn nhất thu được trong 1 tháng của nhà máy A (đơn vị tính là tỉ đồng và kết quả làm tròn đến hàng phần trăm).

Câu 2 :

Một hộ gia đình muốn xây dựng một kho chứa mini dạng khối tứ diện OABC tận dụng góc tường nhà (với O là góc tường, ba cạnh OA, OB, OC nằm trên ba mép tường vuông góc). Để lắp đặt hệ thống thông gió, mặt phía trước của kho (mặt phẳng ABC) bắt buộc phải đi qua một van điều tiết đặt tại vị trí M có tọa độ M(1; 2; 1) (đơn vị tính là mét). Gia đình muốn thiết kế kho sao cho thể tích của kho là nhỏ nhất để không làm ảnh hưởng quá nhiều đến diện tích sinh hoạt của sân chung. Khi kho được thiết kế với thể tích nhỏ nhất, hãy tính khoảng cách từ góc tường O đến mặt phẳng (ABC).

Câu 3 :

Giả sử dân số Việt Nam được dự báo theo mô hình logistic, giai đoạn từ năm 2023 đến hết năm 2035 là hàm số $P(t) = \frac{{120}}{{1 + 0,2{e^{ - 0,06t}}}}$ (triệu người), trong đó t là số năm tính từ đầu năm 2023. Chi phí an sinh xã hội bình quân theo đầu người được mô hình hoá bởi hàm số $C(t) = 25 - 20{e^{ - 0,05t}}$ (triệu đồng/đầu người/năm). Tính tốc độ thay đổi của tổng chi phí an sinh xã hội toàn quốc (nghìn tỷ đồng/năm) vào đầu năm 2030 (làm tròn kết quả đến hàng đơn vị).

Câu 4 :

Trong hệ trục toạ độ Oxy, đơn vị mỗi trục là mét, một đường trượt mới sẽ được xây dựng theo bản thiết kế đã trình bày như hình vẽ. Thanh trượt bắt đầu từ A và kết thúc tại C, đường cong của thanh trượt là một phần của đồ thị hàm số $f\left( x \right) = \frac{{a{x^2} + bx + c}}{{x + d}}$, biết đồ thị hàm số f(x) tiếp xúc với trục Ox tại điểm B.

Bạn Nam bắt đầu trượt từ điểm A, hỏi khi Nam cách vị trí ban đầu theo phương ngang một khoảng 5 mét thì Nam cách mặt đất bao nhiêu mét, biết trục Ox nằm trên mặt đất (kết quả làm tròn đến hàng phần trăm).

Câu 5 :

Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABC.A’B’C’D’ có A(-3; 2; 1), C(4; 2; 0), B’(-2; 1; 1), D’(3; 5; 4). Gọi toạ độ của điểm A’ là A’(a; b; c). Tính giá trị của biểu thức $\frac{{a - b - c}}{2}$.

Câu 6 :

Một mái nhà được tạo bởi hai nửa lục giác đều ABCD, ABC’D’ và hai tam giác bằng nhau ADD’, BCC’. Biết CDD’C’ là hình chữ nhật và AB // CD // C’D’, CD = C’D’ = 2AB = 6 m, DD’ = 4 m. Tìm số đo góc nhị diện [D’, AD, C] (làm tròn kết quả đến hàng đơn vị của độ).

Lời giải và đáp án

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1 :

Dãy số nào sau đây là cấp số cộng?

A.

$\left( u_{n} \right):u_{n} = 2^{n} - 1$.
B.

$\left( u_{n} \right):u_{n} = 2u_{n - 1},\forall n \geq 2$.
C.

$\left( u_{n} \right):u_{n} = u_{n - 1} - 2,\forall n \geq 2$.
D.

$\left( u_{n} \right):u_{n} = \dfrac{1}{n}$.

Đáp án : C

Phương pháp giải :

Nếu ${u_n} - {u_{n - 1}} = d$ (hằng số) thì $\left( {{u_n}} \right)$ là cấp số cộng.

Lời giải chi tiết :

Xét đáp án A:

${u_n} - {u_{n - 1}} = {2^n} - 1 - ({2^{n - 1}} - 1) = {2^{n - 1}}$. Loại.

Xét đáp án B:

${u_n} - {u_{n - 1}} = 2{u_{n - 1}} - {u_{n - 1}} = {u_{n - 1}}$. Loại.

Xét đáp án C:

${u_n} - {u_{n - 1}} = {u_{n - 1}} - 2 - {u_{n - 1}} = - 2$. Nhận vì -2 là hằng số.

Xét đáp án D:

${u_n} - {u_{n - 1}} = \frac{1}{n} - \frac{1}{{n - 1}} = \frac{{ - 1}}{{n(n - 1)}}$. Loại.

Câu 2 :

Cho F(x) là nguyên hàm của hàm số $f(x) = 6x^{5} + \dfrac{1}{x^{3}}$ thỏa mãn F(1) = 0. Tîm F(x).

A.

$F(x) = x^{6} - \dfrac{1}{2x^{2}} + \dfrac{1}{2}$.
B.

$F(x) = x^{6} - \dfrac{1}{2x^{2}} - \dfrac{1}{2}$.
C.

$F(x) = x^{6} + \dfrac{1}{2x^{2}} - \dfrac{3}{2}$.
D.

$F(x) = x^{6} - \dfrac{3}{x^{2}} + 2$.

Đáp án : B

Phương pháp giải :

Áp dụng công thức nguyên hàm của hàm lũy thừa: $\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C$.

Lời giải chi tiết :

$\int {f(x)dx} = \int {\left( {6{x^5} + \frac{1}{{{x^3}}}} \right)dx} $

$= \int {\left( {6{x^5} + {x^{ - 3}}} \right)dx} = {x^6} - \frac{1}{{2{x^2}}} + C$.

$F(1) = 0 \Leftrightarrow {1^6} - \frac{1}{{{{2.1}^2}}} + C = 0 \Leftrightarrow C = - \frac{1}{2}$.

Câu 3 :

Biết ${\int{g(x)dx}} = G(x) + C$ (với C là hằng số). Khi đó khẳng định nào sau đây đúng?

A.

$g'(x) = G(x) + C$.
B.

$G'(x) = g(x) - C$.
C.

$g'(x) = G(x)$.
D.

$G'(x) = g(x)$.

Đáp án : D

Phương pháp giải :

Dựa vào định nghĩa nguyên hàm.

Lời giải chi tiết :

$\int {g(x)dx} = G(x) + C$ khi G’(x) = g(x).

Câu 4 :

Cho bảng phân bố tần số ghép lớp về độ dài của 60 lá dương xỉ trưởng thành như sau:

Tính khoảng tứ phân vị (làm tròn đến chữ số thập phân thứ nhất) của mẫu số liệu trên?

A.

13,7.
B.

13,6.
C.

13,5.
D.

13,8.

Đáp án : A

Phương pháp giải :

Khoảng tứ phân vị: ${\Delta _Q} = {Q_3} - {Q_1}$.

Lời giải chi tiết :

${Q_1} = 20 + \frac{{\frac{{60}}{4} - 7}}{{19}}(30 - 20) = \frac{{460}}{{19}}$.

${Q_3} = 30 + \frac{{\frac{{3.60}}{4} - (7 + 19)}}{{24}}(40 - 30) = \frac{{455}}{{12}}$.

${\Delta _Q} = {Q_3} - {Q_1} = \frac{{3125}}{{228}} \approx 13,7$.

Câu 5 :

Cho hàm số y = f(x) có đạo hàm $f'(x) = (2x - 1)(x + 1)$. Hàm số y = f(x) có giá trị lớn nhất trên [-2; 0] bằng

A.

f(-2).
B.

$f\left( {- \dfrac{1}{2}} \right)$.
C.

f(0).
D.

f(-1).

Đáp án : D

Phương pháp giải :

Lập bảng xét dấu f’(x), từ đó suy ra sự biến thiên của f(x) kết luận GTLN.

Lời giải chi tiết :

Xét trên [-2; 0], ta có: $f'(x) = 0 \Leftrightarrow x = - 1$.

Theo bảng xét dấu, f(x) đạt GTLN trên [-2; 0] bằng f(-1).

Câu 6 :

Số đường tiệm cận của đồ thị hàm số $y = 2x + 3 + \dfrac{1}{x - 1}$ là

A.

3.
B.

0.
C.

1.
D.

2.

Đáp án : D

Phương pháp giải :

Dựa vào đặc điểm đồ thị hàm phân thức hữu tỉ.

Lời giải chi tiết :

Đồ thị hàm số có 1 tiệm cận xiên y = 2x – 3 và 1 tiệm cận đứng x = 1.

Câu 7 :

Cho ${{\log }_{0,2}}x>{{\log }_{0,2}}y$. Chọn khẳng định đúng:

A.

$x > y \geq 0$.
B.

$y > x \geq 0$.
C.

$x > y > 0$.
D.

$y > x > 0$.

Đáp án : D

Phương pháp giải :

$\left\{ \begin{array}{l}{\log _a}x > {\log _a}y\\a < 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x > 0\\y > 0\\x < y\end{array} \right.$.

Lời giải chi tiết :

$\left\{ \begin{array}{l}{\log _{0,2}}x > {\log _{0,2}}y\\0,2 < 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x > 0\\y > 0\\x < y\end{array} \right. \Rightarrow y > x > 0$.

Câu 8 :

Cho hình chóp đều S.ABCD có cạnh đáy 2a, cạnh bên 4a. Tính độ dài đường cao hình chóp.

A.

2a.
B.

$a\sqrt{14}$.
C.

3a.
D.

$a\sqrt{15}$.

Đáp án : B

Phương pháp giải :

Sử dụng tính chất của hình chóp đều, định lý Pythagore để tính đường cao hình chóp.

Lời giải chi tiết :

Gọi O là tâm đáy hình vuông ABCD. Khi đó đường cao hình chóp là SO.

Ta có $AC = 2a\sqrt 2 \Rightarrow AO = a\sqrt 2 $.

Xét tam giác SAO vuông tại O:

$SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{{(4a)}^2} - {{(a\sqrt 2 )}^2}} = a\sqrt {14} $.

Câu 9 :

Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm A(2; 1; -3), đồng thời vuông góc với hai mặt phẳng (Q): x + y + 3z = 0, (R): 2x – y + z = 0 là

A.

4x – 5y – 3z – 8 = 0.
B.

4x + 5y – 3z – 4 = 0.
C.

4x + 5y – 3z – 22 = 0.
D.

4x – 5y – 3z – 12 = 0.

Đáp án : C

Phương pháp giải :

Vecto pháp tuyến của (P) là tích có hướng hai vecto pháp tuyến của (Q) và (R).

Lời giải chi tiết :

Vecto pháp tuyến của (Q), (R) lần lượt là: $\overrightarrow {{n_Q}} = (1;1;3)$, $\overrightarrow {{n_R}} = (2; - 1;1)$.

$\left[ {\overrightarrow {{n_Q}} ,\overrightarrow {{n_R}} } \right] = (4;5; - 3)$ là một vecto pháp tuyến của (P). Phương trình của (P) là:

$4(x - 2) + 5(y - 1) - 3(z + 3) = 0 $

$\Leftrightarrow 4x + 5y - 3z - 22 = 0$.

Câu 10 :

Cho hình hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$. Khẳng định nào dưới đây sai?

A.

$\overset{\rightarrow}{AD} + \overset{\rightarrow}{BB_{1}} = \overset{\rightarrow}{AD_{1}}$.
B.

$\overset{\rightarrow}{AB} + \overset{\rightarrow}{AD} + \overset{\rightarrow}{AA_{1}} = \overset{\rightarrow}{AC_{1}}$.
C.

$\overset{\rightarrow}{AB} + \overset{\rightarrow}{DD_{1}} = \overset{\rightarrow}{AD_{1}}$.
D.

$\overset{\rightarrow}{AB} + \overset{\rightarrow}{CC_{1}} = \overset{\rightarrow}{AB_{1}}$.

Đáp án : C

Phương pháp giải :

Áp dụng khái niệm hai vecto bằng nhau, quy tắc ba điểm và quy tắc hình hộp để biến đổi biểu thức.

Lời giải chi tiết :

Xét đáp án A: $\overrightarrow {AD} + \overrightarrow {B{B_1}} = \overrightarrow {AD} + \overrightarrow {D{D_1}} = \overrightarrow {A{D_1}} $ (đúng).

Xét đáp án B: $\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} = \overrightarrow {A{C_1}} $ (đúng).

Xét đáp án C: $\overrightarrow {AB} + \overrightarrow {D{D_1}} = \overrightarrow {AB} + \overrightarrow {B{B_1}} = \overrightarrow {A{B_1}} \ne \overrightarrow {A{D_1}} $.

Xét đáp án D: $\overrightarrow {AB} + \overrightarrow {C{C_1}} = \overrightarrow {AB} + \overrightarrow {B{B_1}} = \overrightarrow {A{B_1}} $ (đúng).

Câu 11 :

Khoảng cách giữa hai điểm I(1; 4; -3) và K(6; 4; 5) là

A.

$\sqrt{89}$.
B.

$\sqrt{114}$.
C.

$\sqrt{103}$.
D.

$\sqrt{95}$.

Đáp án : A

Phương pháp giải :

$IK = \sqrt {{{({x_K} - {x_I})}^2} + {{({y_K} - {y_I})}^2} + {{({z_K} - {z_I})}^2}} $.

Lời giải chi tiết :

$IK = \sqrt {{{(6 - 1)}^2} + {{(4 - 4)}^2} + {{(5 + 3)}^2}} = \sqrt {89} $.

Câu 12 :

Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án A, B, C, D. Hỏi đó là hàm số nào?

A graph of a function

Description automatically generated

A.

$y = - x^{3} + 3x$.
B.

$y = x^{3} + 2x + 1$.
C.

$y = x^{3} - 3x$.
D.

$y = x^{3} + 3x^{2}$.

Đáp án : C

Phương pháp giải :

Dựa vào hình dạng đồ thị, giao điểm với trục tung, các điểm cực trị để tìm công thức hàm số.

Lời giải chi tiết :

Quan sát đồ thị, thấy $\mathop {\lim }\limits_{x \to + \infty } y = + \infty \Rightarrow $ hệ số của ${x^3}$ dương. Loại đáp án A.

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 0, suy ra hệ số tự do bằng 0. Loại đáp án B.

Xét đáp án C: $y' = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1$.

Xét đáp án D: $y' = 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.$

Vì đồ thị có hai điểm cực trị với hoành độ là 1 và -1 nên hàm số cần tìm là $y = {x^3} - 3x$.

Phần II: Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1 :

a) Hàm số biểu thị tốc độ tăng trưởng lợi nhuận $P'(t) = - 3t^{2} + 20t + 63t$.

Đúng

Sai

b) Lợi nhuận của công ty đạt mức tối đa tại thời điểm t = 9.

Đúng

Sai

c) Tại thời điểm t = 4 thì tốc độ tăng trưởng lợi nhuận là lớn nhất.

Đúng

Sai

d) Lợi nhuận của công ty sau 1 quý là 27 triệu đồng.

Đúng

Sai

Đáp án

a) Hàm số biểu thị tốc độ tăng trưởng lợi nhuận $P'(t) = - 3t^{2} + 20t + 63t$.

Đúng

Sai

b) Lợi nhuận của công ty đạt mức tối đa tại thời điểm t = 9.

Đúng

Sai

c) Tại thời điểm t = 4 thì tốc độ tăng trưởng lợi nhuận là lớn nhất.

Đúng

Sai

d) Lợi nhuận của công ty sau 1 quý là 27 triệu đồng.

Đúng

Sai

Phương pháp giải :

a) Tìm P’(t).

b) Tìm GTLN của P(t) trên [0; 12].

c) Tìm GTLN của P’(t) trên [0; 12].

d) Tính P(3).

Lời giải chi tiết :

a) Sai. Hàm số biểu thị tốc độ tăng trưởng lợi nhuận là $P'(t) = - 3{t^2} + 20t + 63$.

b) Đúng. Xét trên [0; 12]: $P'(t) = - 3{t^2} + 20t + 63 = 0 \Leftrightarrow t = 9$.

Ta có f(0) = -45; f(9) = 603; f(12) = 423. Vậy lợi nhuận của công ty đạt mức tối đa tại thời điểm t = 9.

c) Sai. $P''(t) = - 6t + 20 = 0 \Leftrightarrow t = \frac{{10}}{3}$.

P’(0) = 63; $P'\left( {\frac{{10}}{3}} \right) = \frac{{289}}{3}$; P’(12) = -129. Vậy tại thời điểm $t = \frac{{10}}{3}$ thì tốc độ tăng trưởng lợi nhuận là lớn nhất.

d) Sai. Lợi nhuận của công ty sau 1 quý là P(3) = 207 (triệu đồng).

Câu 2 :

a) Phương sai xấp xỉ 20,52.

Đúng

Sai

Đúng

Sai

c) Tứ phân vị thứ ba là 25.

Đúng

Sai

d) Độ dài mỗi nhóm là 4.

Đúng

Sai

Đáp án

a) Phương sai xấp xỉ 20,52.

Đúng

Sai

Đúng

Sai

c) Tứ phân vị thứ ba là 25.

Đúng

Sai

d) Độ dài mỗi nhóm là 4.

Đúng

Sai

Phương pháp giải :

a) Áp dụng công thức tính phương sai của mẫu số liệu ghép nhóm.

b) Áp dụng công thức tính tứ phân vị thứ ba của mẫu số liệu ghép nhóm.

c) Áp dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm.

d) Để tính độ dài nhóm, ta lấy đầu mút phải trừ đi đầu mút trái của nhóm.

Lời giải chi tiết :

d) Đúng. Độ dài mỗi nhóm là 4.

c) Sai. ${Q_3} = 18 + \frac{{\frac{{500.3}}{4} - (75 + 105)}}{{197}}(22 - 18) = \frac{{4326}}{{197}} \approx 21,96$.

b) Đúng. ${Q_1} = 14 + \frac{{\frac{{500}}{4} - 75}}{{105}}(18 - 14) = \frac{{334}}{{21}} \approx 15,9$.

Độ chênh lệch giá cao nhất và giá thấp nhất là: ${\Delta _Q} = {Q_3} - {Q_1} \approx 6,1$.

a) Đúng. Số trung bình: $\overline x = \frac{{12.75 + 16.105 + 20.197 + 24.80 + 28.43}}{{75 + 105 + 197 + 80 + 43}} = \frac{{9644}}{{500}}$.

Phương sai: ${s^2} = \frac{1}{{500}}\left[ {{{75.12}^2} + {{105.16}^2} + {{197.20}^2} + {{80.24}^2} + {{43.28}^2}} \right] - {\overline x ^2} \approx 20,52$.

Câu 3 :

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c đều dương.

Đúng

Sai

b) Mặt phẳng (ABC) có phương trình $\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1$.

Đúng

Sai

c) Mặt phẳng (ABC) đi qua điểm H(1; 1; 1) sao cho H là trực tâm tam giác ABC là x + y + z – 3 = 0.

Đúng

Sai

d) Mặt phẳng (ABC) đi qua điểm G(1; 2; 3) sao cho G là trọng tâm tam giác ABC là 6x + 3y + 2z + 18 = 0.

Đúng

Sai

Đáp án

Đúng

Sai

b) Mặt phẳng (ABC) có phương trình $\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1$.

Đúng

Sai

c) Mặt phẳng (ABC) đi qua điểm H(1; 1; 1) sao cho H là trực tâm tam giác ABC là x + y + z – 3 = 0.

Đúng

Sai

d) Mặt phẳng (ABC) đi qua điểm G(1; 2; 3) sao cho G là trọng tâm tam giác ABC là 6x + 3y + 2z + 18 = 0.

Đúng

Sai

Phương pháp giải :

b) Lập phương trình mặt phẳng (ABC) theo đoạn chắn.

c) Chứng minh VTPT của (ABC) là , sau đó lập phương trình mặt phẳng (ABC).

d) Từ tọa độ trọng tâm G, tìm tọa độ ba đỉnh A, B, C, từ đó suy ra phương trình mặt phẳng (ABC).

a) Từ tính chất của cấp số cộng, biểu diễn b, c theo a và thay tọa độ điểm M vào phương trình đoạn chắn để tìm a, b, c. Áp dụng công thức tính khoảng cách từ một điểm đến mặt phẳng để tìm m, n.

Lời giải chi tiết :

b) Đúng. Mặt phẳng (ABC) có phương trình $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$.

d) Sai. G là trọng tâm tam giác ABC nên $G\left( {\frac{{a + 0 + 0}}{3};\frac{{0 + b + 0}}{3};\frac{{0 + 0 + c}}{3}} \right) \Rightarrow G\left( {\frac{a}{3};\frac{b}{3};\frac{c}{3}} \right)$.

Mà theo đề bài $G(1;2;3) \Rightarrow a = 3,b = 6,c = 9$.

Vậy (ABC): $\frac{x}{3} + \frac{y}{6} + \frac{z}{9} = 1 \Leftrightarrow 6x + 3y + 2z - 18 = 0$.

c) Đúng. Gọi AF, CE lần lượt là đường cao của tam giác ABC.

OABC là tứ diện có OA, OB, OC đôi một vuông góc, H là trực tâm của tam giác ABC.

$\left. \begin{array}{l}OA \bot (OBC) \Rightarrow OA \bot BC\\AH \bot BC\end{array} \right\} \Rightarrow BC \bot (OAF) \Rightarrow BC \bot OH$ (1)

$\left. \begin{array}{l}OC \bot (OAB) \Rightarrow OC \bot AB\\CE \bot AB\end{array} \right\} \Rightarrow AB \bot (OCE) \Rightarrow AB \bot OH$ (2)

Từ (1) và (2) suy ra $OH \bot (ABC) \Rightarrow \overrightarrow {OH} = (1;1;1)$ là vecto pháp tuyến của mặt phẳng (ABC).

Vậy (ABC): $1(x - 1) + 1(y - 1) + 1(z - 1) = 0 \Leftrightarrow x + y + z - 3 = 0$.

a) Đúng. Vì A(a; 0; 0) nên OA = a, tương tự ta có OB = b, OC = c.

OA, OB, OC có độ dài lần lượt lập thành cấp số cộng có công sai bằng 2, do đó b = a + 2, c = a + 4.

Suy ra (ABC): $\frac{x}{a} + \frac{y}{{a + 2}} + \frac{z}{{a + 4}} = 1$. Mà M(2; -2; 3) thuộc (ABC) nên:

$\frac{2}{a} + \frac{{ - 2}}{{a + 2}} + \frac{3}{{a + 4}} = 1 \Leftrightarrow a = 2 \Rightarrow b = 4,c = 6$.

Vậy (ABC): $\frac{x}{2} + \frac{y}{4} + \frac{z}{6} = 1 \Leftrightarrow 6x + 3y + 2x - 12 = 0$.

$d\left( {D,(ABC)} \right) = \frac{{\left| {6.1 + 3.1 + 2.1 - 12} \right|}}{{\sqrt {{6^2} + {3^2} + {2^2}} }} = \frac{1}{7} \Rightarrow T = m + n = 1 + 7 = 8$.

Câu 4 :

Hỏi trong các mệnh đề dưới đây, mệnh đề nào là đúng, mệnh đề nào là sai?

a) Nếu bơm được 30 phút thì dừng thì lượng nước trong bể chưa đầy bể.

Đúng

Sai

b) Thể tích nước được bơm vào bể trong 5 phút đầu tiên là 90 (lít).

Đúng

Sai

c) Thể tích nước chảy ra từ bể trong 5 phút đầu tiên là 10 (lít).

Đúng

Sai

d) Khi nước chảy vào vừa làm đầy bể, thì đã có nhiều hơn 900 lít nước bị chảy ra ngoài (làm tròn kết quả đến hàng đơn vị).

Đúng

Sai

Đáp án

a) Nếu bơm được 30 phút thì dừng thì lượng nước trong bể chưa đầy bể.

Đúng

Sai

b) Thể tích nước được bơm vào bể trong 5 phút đầu tiên là 90 (lít).

Đúng

Sai

c) Thể tích nước chảy ra từ bể trong 5 phút đầu tiên là 10 (lít).

Đúng

Sai

d) Khi nước chảy vào vừa làm đầy bể, thì đã có nhiều hơn 900 lít nước bị chảy ra ngoài (làm tròn kết quả đến hàng đơn vị).

Đúng

Sai

Phương pháp giải :

b) Tính $\int\limits_0^5 {{L_1}(t)dt} $.

c) Tính $\int\limits_0^5 {{L_2}(t)dt} $.

a) Tính $\int\limits_0^{30} {\left[ {{L_1}(t) - {L_2}(t)} \right]dt} $.

d) Tìm ${t_0}$ sao cho $\int\limits_0^{{t_0}} {\left[ {{L_1}(t) - {L_2}(t)} \right]dt} = 2015$. Tính $\int\limits_0^{{t_0}} {{L_2}(t)dt} $.

Lời giải chi tiết :

b) Đúng. Thể tích nước được bơm vào bể trong 5 phút đầu tiên là:

$\int\limits_0^5 {{L_1}(t)dt} = \int\limits_0^5 {(6t + 3)dt} = 90$ (lít).

c) Sai. Thể tích nước chảy ra từ bể trong 5 phút đầu tiên là:

$\int\limits_0^5 {{L_2}(t)dt} = \int\limits_0^5 {2tdt} = 25$ (lít).

a) Đúng. Thể tích nước trong bể sau 30 phút là:

$\int\limits_0^{30} {\left[ {{L_1}(t) - {L_2}(t)} \right]dt} = \int\limits_0^{30} {(6t + 3 - 2t)dt} = \int\limits_0^{30} {(4t + 3)dt} = 1890$ (lít).

Vậy sau 30 phút bơm thì nước chưa đầy bể vì 1890 < 2015.

d) Đúng. Nước đầy bể thì $\int\limits_0^t {\left[ {{L_1}(t) - {L_2}(t)} \right]dt} = 2015 \Leftrightarrow \int\limits_0^t {(4t + 3)dt} = 2015$

$2{t^2} + 3t = 2015 \Leftrightarrow \left[ \begin{array}{l}t = 31\\t = - \frac{{65}}{2}\end{array} \right.$. Vì t > 0 nên ta nhận nghiệm t = 31.

Vậy nước bơm sau 31 phút thì đầy bể. Lượng nước đã chảy ra ngoài là:

$\int\limits_0^{31} {{L_2}(t)dt} = \int\limits_0^{31} {2tdt} = 961$ (lít) > 900 (lít).

Phần III: Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1 :

Phương pháp giải :

Tìm hàm lợi nhuận của nhà máy A và áp dụng đạo hàm, tìm GTLN.

Đáp án :

Lời giải chi tiết :

Doanh thu nhà máy A:

$x\left( {50 - 0,0002{x^2}} \right) = 50x - 0,0002{x^3}$ (triệu đồng).

Chi phí nguyên liệu: 35x (triệu đồng).

Thuế: $5\% \left( {50x - 0,0002{x^3}} \right)$ (triệu đồng).

Lợi nhuận nhà máy A:

$L(x) = 50x - 0,0002{x^3} - 35x - 5\% \left( {50x - 0,0002{x^3}} \right) - 150 $

$= - 0,00019{x^3} + 12,5x - 150$.

$L'(x) = - 0,00057{x^2} + 12,5 = 0 \Leftrightarrow x \approx 148,09$ (vì x thuộc đoạn [0; 200]).

Ta có L(0) = -150; L(148,09) $ \approx $ 1083,96; L(200) = 830.

Vậy lợi nhuận sau thuế lớn nhất thu được là xấp xỉ 1,08 tỉ đồng.

Câu 2 :

Phương pháp giải :

Lập phương trình (ABC) theo đoạn chắn, áp dụng BĐT AM – GM để tìm thể tích kho nhỏ nhất. Từ đó suy ra các hệ số của phương trình (ABC) và tính khoảng cách.

Đáp án :

Lời giải chi tiết :

Gọi tọa độ các điểm trên các trục là A(a; 0; 0), B(0; b; 0), và C(0; 0; c) với a, b, c > 0.

Mặt phẳng (ABC) là mặt trước của kho, có phương trình theo đoạn chắn là: $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$.

Vì mặt phẳng này đi qua điểm M(1; 2; 1), ta có: $\frac{1}{a} + \frac{2}{b} + \frac{1}{c} = 1$.

Áp dụng BĐT AM – GM cho ba số dương a, b, c:

$\frac{1}{a} + \frac{2}{b} + \frac{1}{c} \ge 3\sqrt[3]{{\frac{1}{a}.\frac{2}{b}.\frac{1}{c}}}$

$ \Leftrightarrow 1 \ge 3\sqrt[3]{{\frac{2}{{abc}}}} \Leftrightarrow \sqrt[3]{{\frac{2}{{abc}}}} \le \frac{1}{3}$

$\Leftrightarrow \frac{2}{{abc}} \le \frac{1}{{27}} \Leftrightarrow abc \ge 54$.

Thể tích kho là: ${V_{OABC}} = \frac{1}{6}abc \ge \frac{1}{6}.54 = 9$.

Dấu “=” xảy ra $ \Leftrightarrow \frac{1}{a} = \frac{2}{b} = \frac{1}{c} = \frac{1}{3} \Leftrightarrow $ a = 3, b = 6, c = 3.

Vậy (ABC): $\frac{x}{3} + \frac{y}{6} + \frac{z}{3} = 1 \Leftrightarrow 2x + y + 2z - 6 = 0$.

$d(O,(ABC)) = \frac{{\left| {2.0 + 1.0 + 2.0 - 6} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = 2$.

Câu 3 :

Phương pháp giải :

Tìm E(t) = P(t).C(t) và tính E’(7).

Đáp án :

Lời giải chi tiết :

Tổng chi phí an sinh xã hội toàn quốc là:

$E(t) = P(t).C(t) = \frac{{120\left( {25 - 20{e^{ - 0,05t}}} \right)}}{{1 + 0,2{e^{ - 0,06t}}}}$ (triệu đồng/năm).

$E'(t) = \frac{{120{e^{ - 0,05t}}.\left( {1 + 0,2{e^{ - 0,06t}}} \right) - 120\left( {25 - 20{e^{ - 0,05t}}} \right).\left( { - 0,012{e^{ - 0,06t}}} \right)}}{{{{\left( {1 + 0,2{e^{ - 0,06t}}} \right)}^2}}}$.

Tính tốc độ thay đổi của tổng chi phí an sinh xã hội toàn quốc (nghìn tỷ đồng/năm) vào đầu năm 2030:

$E'(7) = \frac{{120{e^{ - 0,05.7}}.\left( {1 + 0,2{e^{ - 0,06.7}}} \right) - 120\left( {25 - 20{e^{ - 0,05.7}}} \right).\left( { - 0,012{e^{ - 0,06.7}}} \right)}}{{{{\left( {1 + 0,2{e^{ - 0,06.7}}} \right)}^2}}} \approx 83$ (nghìn tỷ đồng/năm).

Câu 4 :

Phương pháp giải :

Dựa vào các điểm thuộc đồ thị, tìm các hệ số a, b, c, d rồi tính f(5).

Đáp án :

Lời giải chi tiết :

Ta có $f'(x) = \frac{{a{x^2} + 2adx + (bd - c)}}{{{{(x + d)}^2}}}$.

Đồ thị hàm số:

- Đi qua A(0; 10): $f(0) = 10 \Rightarrow \frac{c}{d} = 10 \Rightarrow c = 10d$.

- Đi qua B(10; 0): $f(10) = 0 \Rightarrow 100a + 10b + c = 0 $

$\Leftrightarrow 100a + 10b + 10d = 0 \Leftrightarrow b = - 10a - d$.

- Tiếp xúc với Ox tại B: $a{(10)^2} + 2ad(10) + (bd - c) = 0$

$\Rightarrow 100a + 20ad + bd - c = 0$

$ \Leftrightarrow 100a + 20ad + ( - 10a - d)d - 10d = 0$

$\Leftrightarrow 100a + 10ad - {d^2} - 10d = 0$ (*).

- Đi qua C(15; 1): $f(15) = 1 \Rightarrow \frac{{225a + 15b + c}}{{15 + d}} = 1 $

$\Leftrightarrow 225a + 15b + c = 15 + d$

$ \Leftrightarrow 225a + 15( - 10a - d) + 10d = 15 + d$

$\Leftrightarrow a = \frac{{5 + 2d}}{{25}}$.

Thế vào (*), ta được:

$100.\frac{{5 + 2d}}{{25}} + 10.\frac{{5 + 2d}}{{25}}.d - {d^2} - 10d = 0 \Leftrightarrow d = \pm 10$.

Nếu d = -10 thì tiệm cận đứng của đồ thị là x = 10, điều này vô lí vì B(10; 0). Do đó d = 10.

Ta tính được các giá trị còn lại là a = 1, b = -20, c = 100. Vậy $f\left( x \right) = \frac{{{x^2} - 20x + 100}}{{x + 10}}$.

Nam cách vị trí ban đầu theo phương ngang một khoảng 5 mét tức là x = 5.

Khoảng cách từ Nam đến mặt đất khi đó là: $f\left( 5 \right) = \frac{{{5^2} - 20.5 + 100}}{{5 + 10}} \approx 1,67$ (m).

Câu 5 :

Phương pháp giải :

Đặt $\overrightarrow u = \overrightarrow {AA'}$.

Áp dụng quy tắc hình bình hành tìm $\overrightarrow u $, từ đó suy ra tọa độ điểm A.

Đáp án :

Lời giải chi tiết :

ABCD là hình bình hành nên $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} $

$ \Leftrightarrow \left\{ \begin{array}{l}{x_C} - {x_A} = {x_B} - {x_A} + {x_D} - {x_A}\\{y_C} - {x_A} = {y_B} - {x_A} + {y_D} - {y_A}\\{z_C} - {z_A} = {z_B} - {z_A} + {z_D} - {z_A}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_D} - {x_A} - {x_C} = 0\\{y_B} + {y_D} - {y_A} - {y_C} = 0\\{z_B} + {z_D} - {z_A} - {z_C} = 0\end{array} \right.$ (*)

Đặt $\overrightarrow u = \overrightarrow {BB'} = \overrightarrow {DD'} $

$\Rightarrow \left\{ \begin{array}{l}{x_{B'}} - {x_B} = {x_{\overrightarrow u }}\\{y_{B'}} - {y_B} = {y_{\overrightarrow u }}\\{z_{B'}} - {z_B} = {z_{\overrightarrow u }}\\{x_{D'}} - {x_D} = {x_{\overrightarrow u }}\\{y_{D'}} - {y_D} = {y_{\overrightarrow u }}\\{z_{D'}} - {z_D} = {y_{\overrightarrow u }}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = {x_{B'}} - {x_{\overrightarrow u }}\\{y_B} = {y_{B'}} - {y_{\overrightarrow u }}\\{z_B} = {z_{B'}} - {z_{\overrightarrow u }}\\{x_D} = {x_{D'}} - {x_{\overrightarrow u }}\\{y_D} = {y_{D'}} - {y_{\overrightarrow u }}\\{z_D} = {z_{D'}} - {z_{\overrightarrow u }}\end{array} \right.$

Thay vào (*), được:

$\left\{ \begin{array}{l} - 2{x_{\overrightarrow u }} + {x_{B'}} + {x_{D'}} - {x_A} - {x_C} = 0\\ - 2{y_{\overrightarrow u }} + {y_{B'}} + {y_{D'}} - {y_A} - {y_C} = 0\\ - 2{z_{\overrightarrow u }} + {z_{B'}} + {z_{D'}} - {z_A} - {z_C} = 0\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l} - 2{x_{\overrightarrow u }} + ( - 2) + 3 - ( - 3) - 4 = 0\\ - 2{y_{\overrightarrow u }} + 1 + 5 - 2 - 2 = 0\\ - 2{z_{\overrightarrow u }} + 1 + 4 - 1 - 0 = 0\end{array} \right.$

$\Leftrightarrow \overrightarrow u = (0;1;2) = \overrightarrow {AA'} = (a + 3;b - 2;c - 1)$

$ \Rightarrow a = - 3;b = 3;c = 3 \Rightarrow \frac{{a - b - c}}{2} = - 4,5$.

Câu 6 :

Phương pháp giải :

Gọi M, N lần lượt là trung điểm của DD’, CC’. Do cân tại A nên .

Gọi H là hình chiếu của A xuống MN. Gọi K là hình chiếu của A xuống DC.

Gắn hệ trục toạ độ với H trùng O, HA trùng Oz, HK trùng Ox, HM trùng Oy.

Tính góc nhị diện bằng góc giữa 2 mặt phẳng bằng phương pháp toạ độ trong không gian.

Đáp án :

Lời giải chi tiết :

Gọi M, N lần lượt là trung điểm của DD', CC'. Do $\Delta ADD'$ cân tại A nên $AM \bot DD'$.

Gọi H là hình chiếu của A xuống MN. Gọi K là hình chiếu của A xuống DC.

Khi đó $DK = 1,5; AD = 3 \Rightarrow AK = \sqrt {A{D^2} - D{K^2}} = \frac{{3\sqrt 3 }}{2}$.

$HK = \frac{1}{2}DD' = 2 \Rightarrow AH = \sqrt {A{K^2} - H{K^2}} = \frac{{\sqrt {11} }}{2}$.

$AM = \sqrt {A{D^2} - M{D^2}} = \sqrt {{3^2} - {2^2}} = \sqrt 5$.

$\Rightarrow HM = \sqrt {A{M^2} - A{H^2}} = \frac{3}{2}$.

Gắn hệ trục toạ độ với H trùng O, HA trùng Oz, HK trùng Ox, HM trùng Oy.

Khi đó $A\left( {0;0;\frac{{\sqrt {11} }}{2}} \right), K(2;0;0), M\left( {0;\frac{3}{2};0} \right) \Rightarrow D\left( {2;\frac{3}{2};0} \right)$.

$ \Rightarrow \overrightarrow {AK} \left( {2;0; - \frac{{\sqrt {11} }}{2}} \right);\overrightarrow {DK} \left( {0; - \frac{3}{2};0} \right)$.

$\Rightarrow \overrightarrow {{n_{(ADK)}}} = \left[ {\overrightarrow {AK} ,\overrightarrow {DK} } \right] = \left( { - \frac{{3\sqrt {11} }}{4};0; - 3} \right)$.

Ta có $\overrightarrow {MA} \left( {0; - \frac{3}{2};\frac{{\sqrt {11} }}{2}} \right),\overrightarrow {MD} (2;0;0)$.

$\Rightarrow \overrightarrow {{n_{(AMD)}}} = \left[ {\overrightarrow {MA} ,\overrightarrow {MD} } \right] = \left( {0;\sqrt {11} ;3} \right)$.

$ \Rightarrow \cos (\overrightarrow {{n_{(ADK)}}} ,\overrightarrow {{n_{(AMD)}}} ) = \frac{{ - 9}}{{\sqrt {\frac{{243}}{{16}}} \cdot \sqrt {20} }} = - \frac{{2\sqrt {15} }}{{15}} $.

$\Rightarrow [D',AD,C] \approx {121^o}$.

👉

Giải bài nhanh với AI Hay: