Bài 8 trang 17 SGK Hình học 10
Đề bài
Cho lục giác \(ABCDEF\). Gọi \(M, N, P, Q, R, S\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DE, EF, FA\). Chứng minh rằng hai tam giác \(MPR\) và \(NQS\) có cùng trọng tâm.
Video hướng dẫn giải
Lời giải chi tiết
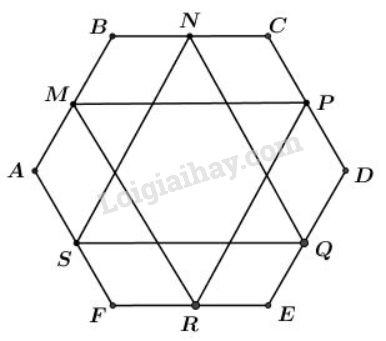
\(MN\) là đường trung bình của tam giác \(ABC\) nên ta có: \(\overrightarrow {MN} = {1 \over 2}\overrightarrow {AC} \)
Tương tự ta có:
\(\eqalign{
& \overrightarrow {PQ} = {1 \over 2}\overrightarrow {CE} \cr
& \overrightarrow {RS} = {1 \over 2}\overrightarrow {EA} \cr} \)
\(\eqalign{
& \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} \cr& = \frac{1}{2}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {CE} + \frac{1}{2}\overrightarrow {EA} \cr&= {1 \over 2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right)\cr& = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {EA} } \right) = {1 \over 2}\overrightarrow {AA} = \overrightarrow 0 \cr
& \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 \cr} \)
Gọi \(G\) là trọng tâm của tam giác \(MPR\), ta có:
\(\overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} = \overrightarrow 0 (2)\)
Mặt khác :
\(\eqalign{
& \overrightarrow {MN} = \overrightarrow {MG} + \overrightarrow {GN} \cr
& \overrightarrow {PQ} = \overrightarrow {PG} + \overrightarrow {GQ} \cr
& \overrightarrow {RS} = \overrightarrow {RG} + \overrightarrow {GS} \cr} \)
\(\Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} \)\( = \left( {\overrightarrow {MG} + \overrightarrow {PG} + \overrightarrow {RG} } \right) \) \( + (\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS}) \)
\( = \overrightarrow 0 + \overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} \) \( = \overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} \)
(vì \(\overrightarrow {MG} + \overrightarrow {PG} + \overrightarrow {RG} \) \(= - \overrightarrow {GM} - \overrightarrow {GP} - \overrightarrow {GR} \) \(= - \left( {\overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} } \right) = \overrightarrow 0 \))
\( \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS}\) \( = \overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} \)
Mà \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0\) nên
\(\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} = \overrightarrow 0 \)
Vậy \(G\) là trọng tâm của tam giác \(NQS.\)
Cách khác:
Gọi G là trọng tâm tam giác MPR \( \Rightarrow \overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} = \overrightarrow 0 \)
Ta cần chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh \( \Rightarrow \overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} = \overrightarrow 0 \)
Thật vậy ta có:
\(\begin{array}{l}2\left( {\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} } \right)\\ = 2\overrightarrow {GN} + 2\overrightarrow {GQ} + 2\overrightarrow {GS} \\ = \left( {\overrightarrow {GB} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {GD} + \overrightarrow {GE} } \right) + \left( {\overrightarrow {GF} + \overrightarrow {GA} } \right)\end{array}\)
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)
\(\begin{array}{l} = \left( {\overrightarrow {GA} + \overrightarrow {GB} } \right) + \left( {\overrightarrow {GC} + \overrightarrow {GD} } \right) + \left( {\overrightarrow {GE} + \overrightarrow {GF} } \right)\\ = 2\overrightarrow {GM} + 2\overrightarrow {GP} + 2\overrightarrow {GR} \end{array}\)
(Vì M, P, R là trung điểm AB, CD, EF)
\(\begin{array}{l} = 2\left( {\overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} } \right)\\ = 2\overrightarrow 0 = \overrightarrow 0 \\ \Rightarrow \overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} = \overrightarrow 0 \end{array}\)
Do đó G cũng là trọng tâm của ΔNQS.
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9 trang 17 SGK Hình học 10
- Bài 7 trang 17 SGK Hình học 10
- Bài 6 trang 17 SGK Hình học 10
- Bài 5 trang 17 SGK Hình học 10
- Bài 4 trang 17 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
- Lý thuyết tích vô hướng của hai vectơ
- Lý thuyết các hệ thức lượng trong tam giác và giải tam giác
- Lý thuyết về số gần đúng - sai số
- Lý thuyết dấu của tam thức bậc hai
- Lý thuyết phương trình đường tròn
- Lý thuyết phương sai và độ lệch chuẩn
- Lý thuyết hệ trục tọa độ
- Lý thuyết số trung bình cộng - số trung vị, mốt
- Lý thuyết về các tập hợp số
- Lý thuyết tổng và hiệu của hai vectơ
