Bài 5 trang 17 SGK Hình học 10
Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng:
Đề bài
Gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\) của tứ giác \(ABCD\). Chứng minh rằng:
\(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Với \(M\) là trung điểm của \(AB\) ta có:
+) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)
+) Với mọi điểm \(O\) bất kì ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} .\)
Lời giải chi tiết
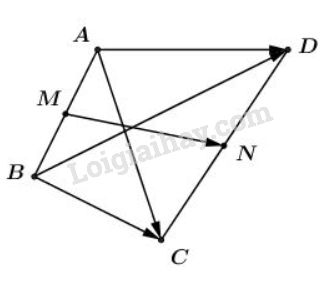
\(N\) là trung điểm của \(CD\) nên ta có:
\( \overrightarrow {MC} + \overrightarrow {MD}=2\overrightarrow {MN} \)
hay \(2\overrightarrow {MN}= \overrightarrow {MC} + \overrightarrow {MD}\) (1)
Theo quy tắc 3 điểm, ta có:
\(\overrightarrow {MC} = \overrightarrow {MA} + \overrightarrow {AC} \) (2)
\(\overrightarrow {MD} = \overrightarrow {MB} + \overrightarrow {BD} \) (3)
Từ (1), (2), (3) ta có:
\(2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {MB} + \overrightarrow {BD} \)
\(= \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \overrightarrow {AC} + \overrightarrow {BD} \) \( = \overrightarrow 0 + \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\) \( = \overrightarrow {AC} + \overrightarrow {BD} \)
(Do M là trung điểm AB nên \({\overrightarrow {MA} + \overrightarrow {MB} }=\overrightarrow {0}\))
Chứng minh tương tự, ta có:
\(\begin{array}{l}
2\overrightarrow {MN} = \overrightarrow {MC} + \overrightarrow {MD} \\
= \left( {\overrightarrow {MB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {MA} + \overrightarrow {AD} } \right)\\
= \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {MA} + \overrightarrow {AD} \\
= \left( {\overrightarrow {MB} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {AD} } \right)\\
= \overrightarrow {BC} + \overrightarrow {AD}
\end{array}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 6 trang 17 SGK Hình học 10
- Bài 7 trang 17 SGK Hình học 10
- Bài 8 trang 17 SGK Hình học 10
- Bài 9 trang 17 SGK Hình học 10
- Bài 4 trang 17 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
