 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Bài 8. Các trường hợp bằng nhau của tam giác vuông
Bài 8. Các trường hợp bằng nhau của tam giác vuông
Bài 64 trang 136 SGK Toán 7 tập 1
Các tam giác vuông ABC và DEF có...
Đề bài
Các tam giác vuông \(ABC\) và \(DEF\) có \(\widehat{A}=\widehat{D}= 90^o\), \(AC=DF.\) Hãy bổ sung thêm một điều kiện bằng nhau để \(\Delta ABC=\Delta DEF\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Lời giải chi tiết
Xem hình vẽ
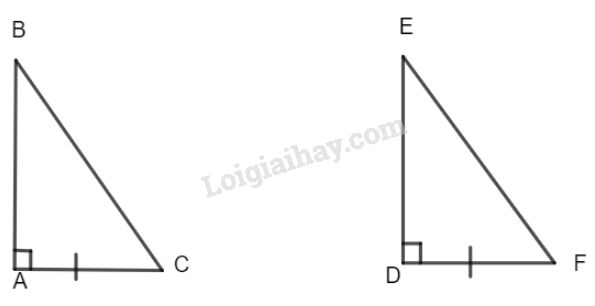
* Trường hợp 1: \(\Delta ABC=\Delta DEF\) theo trường hợp c-g-c
Xét hai tam giác vuông \( ABC\) và \( DEF\) có:
+) \(\widehat{BAC}=\widehat{EDF}=90^0\)
+) \(AC=DF\) (giả thiết)
Bổ sung thêm điều kiện \(AB=DE\) thì \( \Delta ABC= \Delta DEF\) (c-g-c).
* Trường hợp 2: \(\Delta ABC=\Delta DEF\) theo trường hợp g-c-g
Xét hai tam giác vuông \( ABC\) và \( DEF\) có:
+) \(\widehat{BAC}=\widehat{EDF}=90^0\)
+) \(AC=DF\) (giả thiết)
Bổ sung thêm điều kiện \(\widehat{C}=\widehat{F}\) thì \( \Delta ABC= \Delta DEF\) (g-c-g).
* Trường hợp 3: \(\Delta ABC=\Delta DEF\) theo trường hợp cạnh huyền - cạnh góc vuông.
Xét hai tam giác vuông \( ABC\) và \( DEF\) có:
+) \(AC=DF\) (giả thiết)
Bổ sung thêm điều kiện \(BC=EF\) thì \( \Delta ABC= \Delta DEF\) (cạnh huyền - cạnh góc vuông).




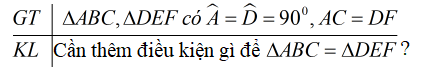








Danh sách bình luận