Bài 6 trang 17 SGK Hình học 10
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho
Đề bài
Cho hai điểm phân biệt \(A\) và \(B\). Tìm điểm \(K\) sao cho:\[3\overrightarrow{KA} + 2\overrightarrow{KB} = \overrightarrow{0}.\]
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Từ đẳng thức đã cho ta biến đổi tương đương đưa về dạng \(\overrightarrow {AK} = k\overrightarrow {AB}\)
Sau đó kết luận vị trí điểm \(K\), trong đó
+) Nếu \(k>0\) thì \(\overrightarrow {AK} \) và \( \overrightarrow {AB}\) cùng hướng.
+) Nếu \(k<0\) thì \(\overrightarrow {Ak} \) và \( \overrightarrow {AB}\) ngược hướng.
Lời giải chi tiết
Ta có: \(3\overrightarrow{KA} + 2\overrightarrow{KB} = \overrightarrow{0}\)
\( \Rightarrow 3\overrightarrow{KA}+2 (\overrightarrow{KA}+\overrightarrow {AB}) = \overrightarrow{0}\)
\( \Rightarrow 5\overrightarrow{KA} +2\overrightarrow {AB} = \overrightarrow{0}\)
\(\Leftrightarrow -5\overrightarrow {AK} + 2\overrightarrow {AB} = \overrightarrow{0} \)
\(\Leftrightarrow 5\overrightarrow {AK} = 2\overrightarrow {AB}\)
\(\Leftrightarrow \overrightarrow {AK} = \frac{2}{5}\overrightarrow {AB}\)
Suy ra \(\overrightarrow {AK} ,\overrightarrow {AB} \) cùng hướng và \(AK = \frac{2}{5}AB \).
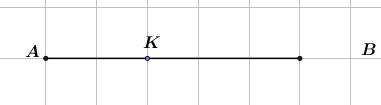
Vậy \(K\) nằm giữa \(A\) và \(B\) sao cho \(AK = \frac{2}{5}AB \).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 7 trang 17 SGK Hình học 10
- Bài 8 trang 17 SGK Hình học 10
- Bài 9 trang 17 SGK Hình học 10
- Bài 5 trang 17 SGK Hình học 10
- Bài 4 trang 17 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
