Bài 4 trang 17 SGK Hình học 10
Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đạn AM. Chứng minh rằng:
Video hướng dẫn giải
Gọi \(AM\) là trung tuyến của tam giác \(ABC\) và \(D\) là trung điểm của đạn \(AM\). Chứng minh rằng:
LG a
\(2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \)
Phương pháp giải:
Với \(M\) là trung điểm của \(AB\) ta có:
+) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)
+) Với mọi điểm \(O\) bất kì ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} .\)
Lời giải chi tiết:
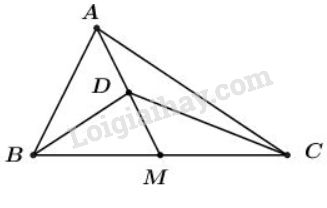
Vì \(M\) là trung điểm của \(BC\) nên:
Ta có:
\(\overrightarrow {DB} + \overrightarrow {DC} = 2\overrightarrow {DM} \)
Mặt khác, do \(D\) là trung điểm của đoạn \(AM\) nên
\(\overrightarrow {DM} = - \overrightarrow {DA} \) \(\Leftrightarrow \overrightarrow {DM} + \overrightarrow {DA} = \overrightarrow 0 \)
Khi đó: \(2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 2\overrightarrow {DA} + 2\overrightarrow {DM} \)\(= 2\left( {\overrightarrow {DA} + \overrightarrow {DM} } \right) = \overrightarrow 0 \)
LG b
\(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \), với \(O\) là điểm tùy ý.
Phương pháp giải:
Với \(M\) là trung điểm của \(AB\) ta có:
+) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)
+) Với mọi điểm \(O\) bất kì ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} .\)
Lời giải chi tiết:
Ta có:
Cách khác:
\(\eqalign{
& 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \cr} \)
\(\begin{array}{l}
\Leftrightarrow 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} - 4\overrightarrow {OD} = \overrightarrow 0 \\
\Leftrightarrow 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} - 2\overrightarrow {OD} - \overrightarrow {OD} - \overrightarrow {OD} = \overrightarrow 0 \\
\Leftrightarrow \left( {2\overrightarrow {OA} - 2\overrightarrow {OD} } \right) + \left( {\overrightarrow {OB} - \overrightarrow {OD} } \right) + \left( {\overrightarrow {OC} - \overrightarrow {OD} } \right) = \overrightarrow 0 \\
\Leftrightarrow 2\left( {\overrightarrow {OA} - \overrightarrow {OD} } \right) + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \\
\Leftrightarrow 2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0
\end{array}\)
(Đúng theo câu a)
Vậy: \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \), với \(O\) là điểm tùy ý
Loigiaihay.com





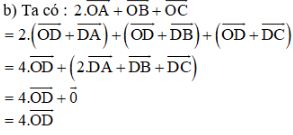








Danh sách bình luận