 Toán 11, giải toán lớp 11 chân trời sáng tạo
Toán 11, giải toán lớp 11 chân trời sáng tạo
 Bài 2. Trung vị và tứ phân vị của mẫu số liệu ghép nhóm..
Bài 2. Trung vị và tứ phân vị của mẫu số liệu ghép nhóm..
Bài 4 trang 141 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cân nặng của một số lợn con mới sinh thuộc hai giống A và B được cho ở biểu đồ dưới đây (đơn vị: kg).
Đề bài
Cân nặng của một số lợn con mới sinh thuộc hai giống A và B được cho ở biểu đồ dưới đây (đơn vị: kg).
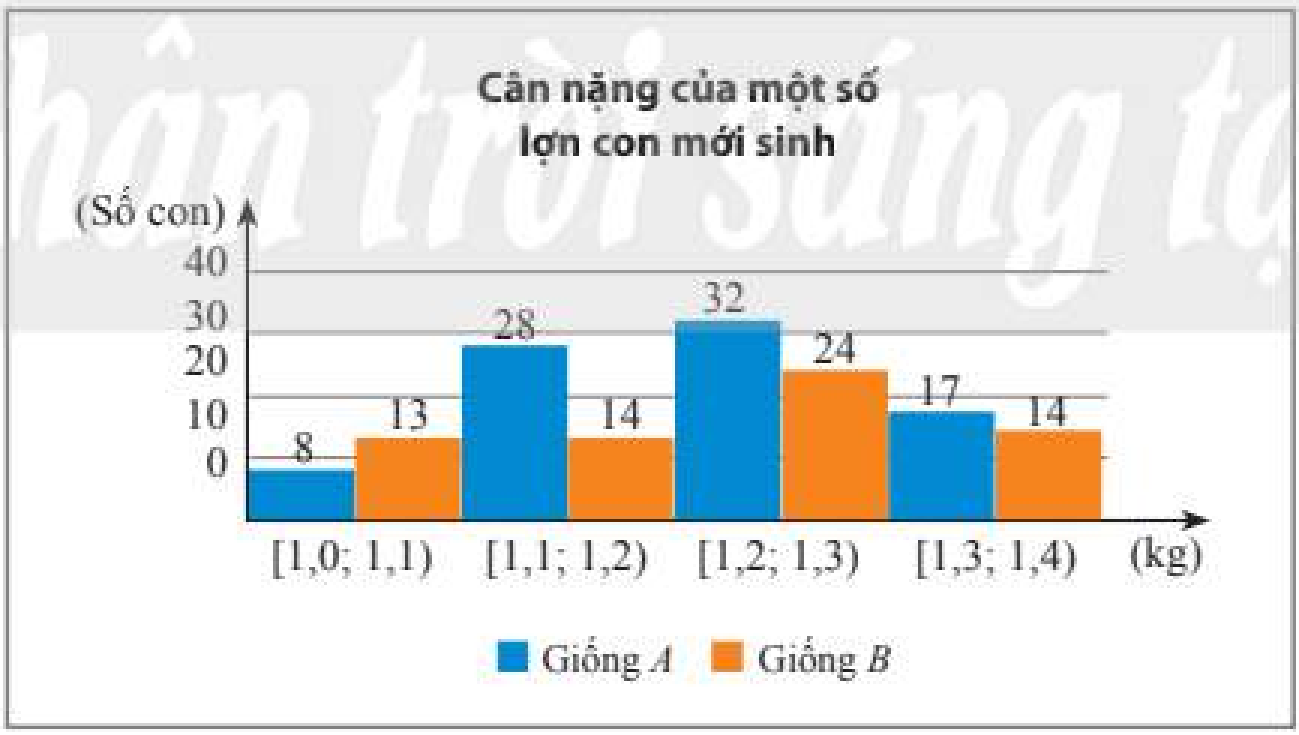
a) Hãy so sánh cân nặng của lợn con mới sinh giống A và giống B theo số trung bình và trung vị.
b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của cân nặng lợn con mới sinh giống A và của cân nặng lợn con mới sinh giống B.
Phương pháp giải - Xem chi tiết
Lập bảng tần số ghép nhóm rồi tính số trung bình, số trung vị, tứ phân vị thứ nhất và thứ ba theo bảng tần số ghép nhóm rồi so sánh.
Lời giải chi tiết
Ta có số liệu thống kê cân nặng của một số lợn con mới sinh thuộc hai giống A và B như sau:
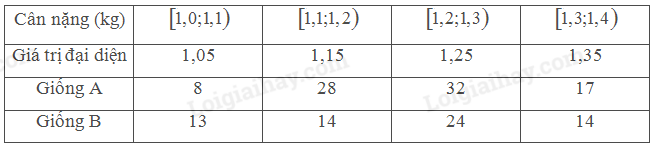
• Tổng số lợn con giống A là: \(n = 8 + 28 + 32 + 17 = 85\)
Cân nặng trung bình của lợn con giống A là:
\(\bar x = \frac{{8.1,05 + 28.1,15 + 32.1,25 + 17.1,35}}{{85}} \approx 1,22\left( {kg} \right)\)
Nhóm chứa số trung vị của giống A là: \(\begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array}\)
Ta có: \(n = 85;{n_m} = 32;C = 8 + 28 = 36;{u_m} = 1,2;{u_{m + 1}} = 1,3\)
Trung vị của cân nặng của lợn con giống A là:
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,2 + \frac{{\frac{{85}}{2} - 36}}{{32}}.\left( {1,3 - 1,2} \right) \approx 1,22\left( {kg} \right)\)
• Tổng số lợn con giống B là: \(n = 13 + 14 + 24 + 14 = 65\)
Cân nặng trung bình của lợn con giống B là:
\(\bar x = \frac{{13.1,05 + 14.1,15 + 24.1,25 + 14.1,35}}{{65}} = 1,21\left( {kg} \right)\)
Nhóm chứa số trung vị của giống B là: \(\begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array}\)
Ta có: \(n = 65;{n_m} = 24;C = 13 + 14 = 27;{u_m} = 1,2;{u_{m + 1}} = 1,3\)
Trung vị của cân nặng của lợn con giống B là:
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,2 + \frac{{\frac{{65}}{2} - 27}}{{24}}.\left( {1,3 - 1,2} \right) \approx 1,22\left( {kg} \right)\)
Vậy số cân nặng trung bình của giống A lớn hơn giống B, số trung vị của giống A và giống B xấp xỉ bằng nhau.
b)
• Giống A
Gọi \({x_1};{x_2};...;{x_{85}}\) là cân nặng của các con lợn con được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,0;1,1} \right)}\end{array}}\end{array};{x_9},...,{x_{36}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,1;1,2} \right)}\end{array}}\end{array}}\end{array};{x_{37}},...,{x_{68}} \in \begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array};{x_{69}},...,{x_{85}} \in \begin{array}{*{20}{l}}{\;\left[ {1,3;1,4} \right)}\end{array}\)
Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\).
Ta có: \(n = 85;{n_m} = 28;C = 8;{u_m} = 1,1;{u_{m + 1}} = 1,2\)
Do \({x_{21}},{x_{22}} \in \begin{array}{*{20}{c}}{\left[ {1,1;1,2} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,1 + \frac{{\frac{{85}}{4} - 8}}{{28}}.\left( {1,2 - 1,1} \right) \approx 1,15\)
Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\).
Ta có: \(n = 85;{n_j} = 32;C = 8 + 28 = 34;{u_j} = 1,2;{u_{j + 1}} = 1,3\)
Do \({x_{64}},{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,2;1,3} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,2 + \frac{{\frac{{3.85}}{4} - 34}}{{32}}.\left( {1,3 - 1,2} \right) \approx 1,29\)
• Giống B
Gọi \({y_1};{y_2};...;{y_{65}}\) là cân nặng của các con lợn con được xếp theo thứ tự không giảm.
Ta có:
\({y_1},...,{y_{13}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,0;1,1} \right)}\end{array}}\end{array};{y_{14}},...,{y_{27}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,1;1,2} \right)}\end{array}}\end{array}}\end{array};{y_{28}},...,{y_{51}} \in \begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array};{y_{52}},...,{y_{65}} \in \begin{array}{*{20}{l}}{\;\left[ {1,3;1,4} \right)}\end{array}\)
Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{y_{16}} + {y_{17}}} \right)\).
Ta có: \(n = 65;{n_m} = 14;C = 13;{u_m} = 1,1;{u_{m + 1}} = 1,2\)
Do \({y_{16}},{y_{17}} \in \begin{array}{*{20}{c}}{\left[ {1,1;1,2} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,1 + \frac{{\frac{{65}}{4} - 13}}{{14}}.\left( {1,2 - 1,1} \right) \approx 1,12\)
Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{y_{49}} + {y_{50}}} \right)\).
Ta có: \(n = 65;{n_j} = 24;C = 13 + 14 = 27;{u_j} = 1,2;{u_{j + 1}} = 1,3\)
Do \({y_{49}},{y_{50}} \in \begin{array}{*{20}{c}}{\left[ {1,2;1,3} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,2 + \frac{{\frac{{3.65}}{4} - 27}}{{24}}.\left( {1,3 - 1,2} \right) \approx 1,29\)
- Bài 3 trang 141 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 2 trang 140 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 1 trang 140 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải mục 2 trang 138, 139, 140 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải mục 1 trang 136, 137 SGK Toán 11 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 136 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 130 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 121 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 113 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 107 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 136 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 130 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 121 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 113 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 107 SGK Toán 11 tập 1 - Chân trời sáng tạo












Danh sách bình luận