Bài 2 trang 79 SGK Toán 11 tập 2 - Cánh Diều

Trong Hình 7 cho ABB’A’, BCC’B’, ACC’A’ là các hình chữ nhật. Chứng minh rằng (AB bot CC',,,,AA' bot BC)

Đề bài

Trong Hình 7 cho ABB’A’, BCC’B’, ACC’A’ là các hình chữ nhật. Chứng minh rằng \(AB \bot CC',\,\,\,AA' \bot BC\)

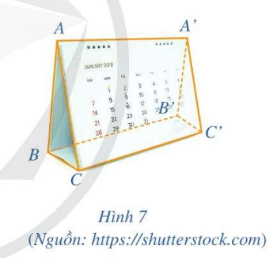
Phương pháp giải - Xem chi tiết

Dựa vào kiến thức hai đường thẳng vuông góc để xác định

Lời giải chi tiết

- Chứng minh \(AB \bot CC'\)

+ Do ABB’A’ là hình chữ nhật \( \Rightarrow AB \bot BB'\) (1)

+ Do BCC’B’ là hình chữ nhật \( \Rightarrow BB' //CC'\) (2)

Từ (1) và (2) \( \Rightarrow AB \bot CC'\) (đpcm)

Chứng minh tương tự:

+ Do BCC’B’ là hình chữ nhật \( \Rightarrow BC \bot CC'\)

+ Do AA'C'C là hình chữ nhật \( \Rightarrow AA' //CC'\)

Từ đó \( \Rightarrow AA' \bot BC\) (đpcm)

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 6 phiếu

Bài 3 trang 79 SGK Toán 11 tập 2 - Cánh Diều
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và (widehat {SAB} = 100^circ ) (Hình 8) .
Bài 4 trang 79 SGK Toán 11 tập 2 - Cánh Diều
Bạn Hoa nói rằng: “Nếu hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c thì a và b vuông góc với nhau”.
Bài 1 trang 79 SGK Toán 11 tập 2 - Cánh Diều
Hình 6 gợi nên hình ảnh 5 cặp đường thẳng vuông góc. Hãy chỉ ra 5 cặp đường thẳng đó
Giải mục 2 trang 78 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 1 ở phần mở đầu, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc. Góc giữa a và b bằng bao nhiêu độ?
Giải mục 1 trang 77 SGK Toán 11 tập 2 - Cánh Diều
Trong mặt phẳng cho hai đường thẳng a, b.
Giải hoạt động mở đầu trang 77 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 1, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc trong không gian.
Lý thuyết Hai đường thẳng vuông góc - Toán 11 Cánh diều
1. Góc giữa hai đường thẳng trong không gian Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu (a, b) hoặc \(\widehat {(a,b)}\).