Bài 1. Góc lượng giác. Giá trị lượng giác của góc lượng..

Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều

Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right)\), \(\left( {OA,ON} \right)\), \(\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2}\); \(\frac{{7\pi }}{6}\); \( - \frac{\pi }{6}\).

Phương pháp giải - Xem chi tiết

Biểu diễn các điểm trên đường tròn lượng giác theo yêu cầu đề bài.

Lời giải chi tiết

- Ta có \((OA, OM) = \alpha = \frac{\pi}{2}\) là góc lượng giác có tia đầu là tia \(OA\), tia cuối là tia \(OM\) và quay theo chiều dương một góc \(\frac{\pi}{2}\), khi đó tia \(OM\) trùng với tia \(OB\).

Điểm \(M\) trên đường tròn lượng giác sao cho \((OA, OM) = \alpha = \frac{\pi}{2}\) được biểu diễn trùng với điểm \(B\).

- Ta có \((OA, ON) = \beta = \frac{7\pi}{6} = \pi + \frac{\pi}{6}\) là góc lượng giác có tia đầu là tia \(OA\), tia cuối là tia \(ON\) và quay theo chiều dương một góc \(\frac{7\pi}{6}\).

- Ta có \((OA, OP) = \gamma = -\frac{\pi}{6}\) là góc lượng giác có tia đầu là tia \(OA\), tia cuối là tia \(OP\) và quay theo chiều âm một góc \(\frac{\pi}{6}\).

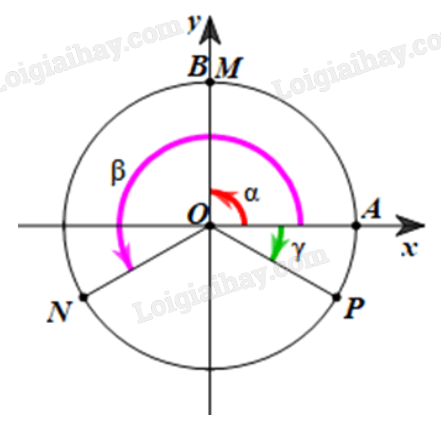
Ba điểm \(M\), \(N\), \(P\) trên đường tròn lượng giác được biểu diễn như hình vẽ dưới đây:

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 14 phiếu

Bài tiếp theo

Bài 2 trang 15 SGK Toán 11 tập 1 - Cánh Diều
Tính các giá trị lượng giác của mỗi góc sau: (225^circ ; - 225^circ ; - 1035^circ );(frac{{5pi }}{3};frac{{19pi }}{2}; - frac{{159pi }}{4})
Bài 3 trang 15 SGK Toán 11 tập 1 - Cánh diều
Tính các giá trị lượng giác (nếu có) có mỗi góc sau:
Bài 4 trang 15 SGK Toán 11 tập 1 - Cánh diều
Tính các giá trị lượng giác của góc (alpha ) trong mỗi trường hợp sau:
Bài 5 trang 15 SGK Toán 11 tập 1 - Cánh diều
Cho α + β = π. Tính: a) A = sin2α + cos2β; b) B = (sinα + cosβ)2 + (cosα + sinβ)2.
Bài 6 trang 15 SGK Toán 11 tập 1 - Cánh diều
Một vệ tinh được định vị tại vị trí A trong không gian.
Giải mục 2 trang 9, 10, 11, 12, 13, 14 SGK Toán 11 tập 1 - Cánh Diều
Hoạt động 6: a) Trong mặt phẳng tọa độ ( định hướng) Oxy, hãy vẽ đường tròn tâm O với bán kính bằng 1.
Giải mục 1 trang 5, 6, 7, 8, 9 SGK Toán 11 tập 1 - Cánh Diều
Hoạt động 1: Nêu định nghĩa góc trong hình học phẳng.
Giải câu hỏi mở đầu trang 5 SGK Toán 11 tập 1 - Cánh diều
Trên mặt chiếc đồng hồ, kim giây đang ở vị trí ban đầu chỉ vào số 3 (Hình 1). Kim giây quay ba vòng và một phần tư vòng (tức là \(3\frac{1}{4}\) vòng) đến vị trí cuối chỉ vào số 6. Khi quay như thế, kim giây đã quét một góc với tia đầu chỉ vào số 3, tia cuối chỉ vào số 6.
Lý thuyết Góc lượng giác. Giá trị lượng giác của góc lượng giác - SGK Toán 11 Cánh Diều
I. Góc lượng giác