 Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
 Bài 4. Số phần tử của một tập hợp. Tập hợp con
Bài 4. Số phần tử của một tập hợp. Tập hợp con
Lý thuyết số phần tử của một tập hợp, tập hợp con
Một tập hơp có thể có một phần tử,có nhiều phần tử, có vô số
Số phần tử của một tập hợp
Một tập hợp có thể có một phần tử,có nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào.
Tập hợp không có phần tử nào được gọi là tập hợp rỗng và được kí hiệu là \(\emptyset \)
Ví dụ: Tập hợp \(A = \left\{ {x;y;z} \right\}\) có ba phần từ là \(x;y;z\)
Tập hợp các số tự nhiên nằm giữa 5 và 6 là tập rỗng \(\emptyset \) vì không có số tự nhiên nào nằm giữa 2 số 5 và 6.
Tập hợp con
Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B. Kí hiệu: A ⊂ B hay B 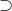 A và đọc là: A là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.
A và đọc là: A là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.
Ví dụ: Cho hai tập hợp \(A = \left\{ {1;2;3} \right\};B = \left\{ {1;2;3;4;5} \right\}\). Khi đó ta thấy mọi phần tử của tập hợp A đều là phần tử cảu tập hợp B nên A là tập con của B, hay \(A \subset B\)
Chú ý:
Nếu \( A \subset B\) và \( B \subset A\) thì ta nói A và B là hai tập hợp bằng nhau, kí hiệu A=B.
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận