 Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
 Đề cương ôn tập học kì 2
Đề cương ôn tập học kì 2
Đề cương ôn tập phần bài tập học kì 2 toán 6
Tổng hợp kiến thức cần nắm vững, các dạng bài tập và câu hỏi có khả năng xuất hiện trong đề thi HK2 môn toán 6 sắp tới
Đại số
Dạng 1: Tính giá trị biểu thức:
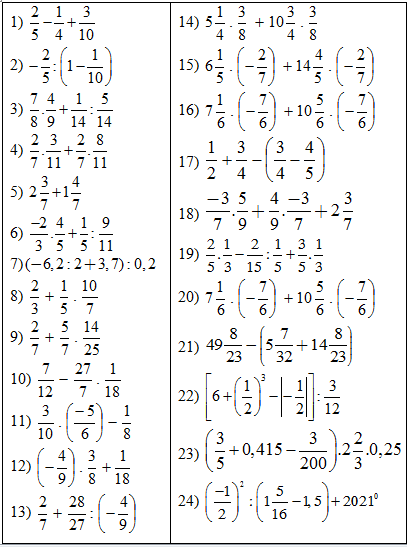
Dạng 2: Tìm x
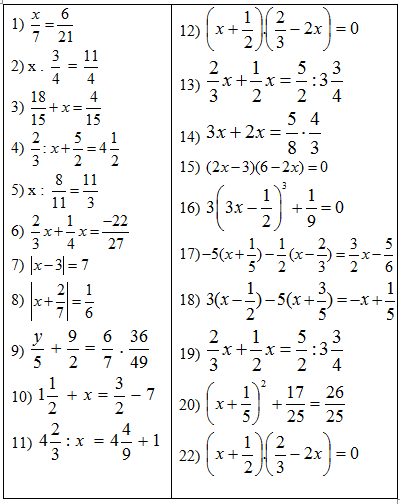
Dạng 3: Toán có lời văn
Bài 1: Lớp 6A có 35 học sinh, kết qủa học lực được xếp thành ba loại: Giỏi, Khá và Trung bình. Số học sinh giỏi chiếm \(\dfrac{1}{7}\)số học sinh cả lớp. Số học sinh Khá chiếm 40% số học sinh còn lại. Tính số học sinh xếp loại trung bình của lớp 6A.
Bài 2: Một cửa hàng bán 80m vải gồm 3 loại: màu trắng, màu xanh, màu vàng. Trong đó số vải trắng bằng \(\dfrac{2}{5}\)số vải, số vải màu xanh chiếm \(\dfrac{1}{6}\) số vải còn lại. Tính số mét vải màu vàng còn lại.
Bài 3: Một hình chữ nhật có chiều dài bằng 30m, chiều rộng bằng 75% chiều dài. Tính chu vi và diện tích hình chữ nhật đó.
Bài 4: Một lớp có 42 học sinh. Số học sinh nữ chiếm \(\dfrac{3}{4}\)số học sinh nam cả lớp. Tính số học sinh nam của lớp đó.
Bài 5: Để giúp đỡ học sinh nghèo, các bạn học sinh của ba lớp 6 đã quyên góp được một số quyển vở. Lớp 6A quyên góp được 72 quyển vở. Số quyển vở lớp 6B quyên góp được bằng \(\dfrac{5}{6}\) của lớp 6A và bằng 80% của lớp 6C. Hỏi cả ba lớp quyên góp được bao nhiêu quyển vở ?
Bài 6: Một thùng gạo có 30 kg gạo. Lần thứ nhất người ta lấy đi \(\dfrac{3}{5}\) số đó. Lần thứ hai người ta tiếp tục lấy đi\(\dfrac{5}{6}\)số gạo còn lại. Hỏi cuối cùng trong thùng còn lại bao nhiêu ki-lô-gam gạo?
Bài 7: Một khu đất hình chữ nhật có chiều dài \(\dfrac{3}{4}\) km và chiều rộng \(\dfrac{5}{8}\) km. Tính chu vi và diện tích của khu đất đó theo đơn vị mét (m).
Bài 8: Một khu đất hình chữ nhật có diện tích là 3 km2 và chiều rộng \(\dfrac{1}{2}\) km. Tính chu vi và diện tích của khu đất đó theo đơn vị mét (m).
Bài 9: Một quyển sách có 240 trang. Ngày đầu Hạnh đọc được 25% số trang, ngày thứ hai đọc được \(\dfrac{4}{9}\) số trang còn lại. Hỏi sau hai ngày còn lại bao nhiêu trang Hạnh chưa đọc ?
Bài 10: Một vườn trường trước đây là hình vuông có chu vi 84 m, nay mở rộng thành hình chữ nhật có chiều dài gấp 2,5 lần cạnh vườn ban đầu, chiều rộng bằng \(\dfrac{5}{3}\) lần cạnh vườn ban đầu. Tính diện tích phần mở rộng thêm.
Bài 11: Số học sinh giỏi và khá của 1 trường là 688, biết rằng số học sinh giỏi bằng 72% số học sinh khá. Hỏi số học sinh mỗi loại khá, giỏi của trường là bao nhiêu?
Dạng 4: Một số bài toán nâng cao
Bài 1: Tính tổng
A = \(\dfrac{1}{{3.5}} + \dfrac{1}{{5.7}} + \dfrac{1}{{7.9}} + ... + \dfrac{1}{{37.39}}\)
Bài 2: Tính tổng
B = \(\dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + \dfrac{1}{{5.6}} + ... + \dfrac{1}{{95.96}}\)
Bài 3: Tính nhanh \(C=\left( {1 - \dfrac{1}{2}} \right)\left( {1 - \dfrac{1}{3}} \right)\left( {1 - \dfrac{1}{4}} \right)...\left( {1 - \dfrac{1}{{2011}}} \right)\)
Bài 4: Tính nhanh \(1\dfrac{1}{2}.1\dfrac{1}{3}.1\dfrac{1}{4}.1\dfrac{1}{5}...1\dfrac{1}{{999}}\)
Bài 5: Cho biểu thức A = \(\dfrac{{19}}{{n + 2}}\).
a) Số nguyên n phải có điều kiện gì để A là phân số.
b) Tìm n để A là số nguyên.
Bài 6: Tìm phân số \(\dfrac{a}{b}\) bằng phân số \(\dfrac{{18}}{{27}}\), biết ƯCLN( a , b ) = 13.
Bài 7: Chứng tỏ rằng: \(\dfrac{{14n + 3}}{{21n + 5}}\) là phân số tối giản với mọi n \( \in \)\(\mathbb{Z}\).
Bài 8: Thực hiện phép tính: \(\left( {\dfrac{{1975}}{{1976}} + \dfrac{{2010}}{{2011}} + \dfrac{{1963}}{{1968}}} \right).\left( {\dfrac{1}{3} - \dfrac{1}{4} - \dfrac{1}{{12}}} \right)\).
Hình học
Bài 1: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Ot, Oy sao cho \(\widehat {xOt} = {25^0}\),\(\widehat {xOy} = {50^0}\).
a. Tia Ot có nằm giữa hai tia Ox và Oy không?
b. So sánh góc tOy và góc xOt.
c. Tia Ot có phải là tia phân giác của góc xOy không? vì sao?
Bài 2: Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết \(\widehat {xOy} = {30^0}\), \(\widehat {xOz} = {120^0}\).
a. Tính số đo góc yOz.
b. Vẽ tia phân giác Om của \(\widehat {yOz}\). Tính số đo góc xOm.
c. Vẽ tia phân giác On của \(\widehat {xOz}\). Tính số đo góc mOn.
Bài 3: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy, Oz sao cho \(\widehat {xOy} = {40^0}\),\(\widehat {xOz} = {110^0}\).
a. Tính số đo góc yOz.
b. Vẽ tia Om là tia đối của tia Ox. Tính số đo góc zOm.
c. Tia Oz có phải là tia phân giác của góc yOm không? vì sao?
Bài 4: Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox.
Biết \(\widehat {xOy} = {30^0}\), \(\widehat {xOz} = {80^0}\).
a. Tính số đo góc yOz.
b. Vẽ tia phân giác Om của \(\widehat {xOy}\). Vẽ tia phân giác On của \(\widehat {yOz}\). Tính số đo góc mOn.
Bài 5: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy, Oz sao cho \(\widehat {xOy} = {140^0}\),\(\widehat {xOz} = {70^0}\).
a. Chứng tỏ Oz là tia phân giác của góc xOy.
b. Vẽ Ot là tia đối của tia Ox. Tính số đo của góc yOt.
Bài 6: Cho hai góc kề bù xOy và yOz, biết góc \(\widehat {xOy} = {40^0}\).
a. Tính số đo góc yOz.
b. Vẽ tia Ot là tia phân giác của góc yOz. Tính số đo góc yOt, góc xOt.
Bài 7: Cho\(\widehat {xOt} = {30^0}\). Vẽ góc yOt kề bù với góc xOt .
a. Tính số đo góc yOt.
b. Vẽ tia phân giác Om của góc xOy. Tính số đo góc xOm. Góc yOm là góc gì ?
Bài 8: Trên cùng nửa mặt phẳng có bờ chưa tia Ox.Về hai tia Oy, Oz sao cho góc\(\widehat {xOz}{\rm{ }} = {\rm{ }}{40^0}\), góc \(\widehat {xOy} = {110^0}\)
a. Tính số đo góc yOz.
b. Vẽ tia Ot là tia đối của tia Ox. Chứng minh tia Oy là tia phân giác của góc Oz.
Bài 9: Trên cùng nửa mặt phẳng có bờ chưa tia Ox.Về hai tiaby, Otsao cho góc \(\widehat {xOt} = {72^0}\), góc \(\widehat {xOy} = {118^0}\).
a. Tính số đo góc yOt.
b. Vẽ tia phân giác Om của góc xOy. Tính số đo góc mOx, góc mOt?
Bài 10. Cho hai tia Oy, Oz cùng nằm trên nửa mặt phẳng có bờ chưa tia Ox.Biết \(\widehat {xOy} = {30^0},\) và \(\widehat {xOz} = {120^0}\).
a. Tính số đo góc yOz. Góc yOz là góc gì?
b. Vẽ tia phân giác Om của góc xOz. Tính số đo góc xOm, góc xOm.
Bài 11: Vẽ góc vuông xOy.Vẽ tia Ozsao cho Ox, Oy cùng nằm trên nửa mặt phẳng có bờ chưa tia Ox. Biết\({\rm{ }}\widehat {xOz} = {30^0}.\)
a. Tính số đo góc yOz.
b. Vẽ Ot là tia phân giác của góc xOz. Tính số đo góc yOt.
Bài 12: Cho góc bẹt xOy.Vẽ tia Oz sao cho \(\widehat {yOz} = {60^0}.\)
a. Tính số đo góc zOx.
b. Vẽ tia Om, On lần lượt là tia phân giác của góc xOz và góc yOz. Hai góc Om và zOn có quan hệ gì? Giải thích?
Bài 13: Cho hai góc kề bù xOy và yOz biết \(\widehat {xOy} = 60^\circ .\)
a. Tính số đo góc yOz.
b. Gọi Oa là tia phân giác của góc yOz, Ob là tia phân giác của góc aOz. Góc bOx là góc gì ? Giải thích vì sao?
Bài 14: Cho \(\widehat {xOy} = {120^0}.\)Vẽ Oz là tia đối của tia Ox, vẽ tia Ot trên cùng nửa mặt phẳng bờ chưa tia Ox sao cho \(\widehat {zOt} = {130^0}\).
a. Tính số đo góc yOz.
b. Chứng minh tia Oy nằm giữa hai tia Ox, Ot?
c. Tính số đo góc xOt.
Loigiaihay.com
Các bài khác cùng chuyên mục











Danh sách bình luận