Đề kiểm tra giữa kì II Toán 6 - Đề số 3 có lời giải chi tiết
Đề kiểm tra giữa kì 2 toán 6 - Đề số 4 có lời giải chi tiết
Đề bài
Câu 1 (1 điểm): Tính:
a) \(\left( { - 2018} \right) - \left( {512 - 2018} \right) + 612\)
b) \(\left| { - 15} \right| - \left( {28 + \left( { - 3} \right)} \right) + \left( { - 28 + 8} \right).3\)
Câu 2 (1 điểm): Rút gọn:
a) \(\frac{{ - 16}}{{72}}\) b) \(\frac{{4.15}}{{3.12}}\)
Câu 3 (2 điểm): Tính:
a) \(\frac{{ - 9}}{{15}} + \frac{{ - 6}}{{15}}\)
b) \(\frac{{15}}{{20}} + \frac{7}{4}\)
c) \(\frac{{ - 4}}{{16}} + \frac{{ - 3}}{8}\)
d) \(\frac{2}{{12}} + \frac{7}{{24}}\)
Câu 4 (2 điểm): Tìm số nguyên \(x\) biết:
a) \(5 - 2x = - 21\)
b) \(\frac{{ - 3}}{x} = \frac{3}{5} + \frac{{ - 9}}{{20}}\)
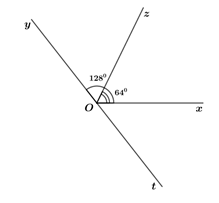
Câu 5 (4 điểm): Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\), vẽ hai tia \(Oy\) và \(Oz\) sao cho \(\angle xOy = {128^0}\), \(\angle xOz = {64^0}\).
a) Trong ba tia \(Ox,\,\,Oy,\,\,Oz\) thì tia nào nằm giữa hai tia còn lại?
b) Tính số đo \(\angle yOz\).
c) Tia \(Oz\) có phải là tia phân giác của góc \(xOy\) không? Vì sao?
d) Gọi \(Ot\) là tia đối của tia \(Oy\). Tính số đo góc \(\angle xOt\).
Lời giải chi tiết
Câu 1 (VD)
Phương pháp:
a) Áp dụng quy tắc dấu ngoặc. Nhóm các số hạng là số đối của nhau.
b) Áp dụng quy tắc thứ tự thực hiện phép tính.
Cách giải:
Tính:
a) \(\left( { - 2018} \right) - \left( {512 - 2018} \right) + 612\)
\(\begin{array}{l}\,\,\,\,\left( { - 2018} \right) - \left( {512 - 2018} \right) + 612\\ = \left( { - 2018} \right) - 512 + 2018 + 612\\ = \left[ {\left( { - 2018} \right) + 2018} \right] + \left( { - 512 + 612} \right)\\ = 100\end{array}\)
\(\begin{array}{l}\,\,\,b) \left| { - 15} \right| - \left( {28 + \left( { - 3} \right)} \right) + \left( { - 28 + 8} \right).3\\ = 15 - 25 + \left( { - 20} \right).3\\ = \left( { - 10} \right) + \left( { - 60} \right)\\ = - 70\end{array}\)
Câu 2 (TH)
Phương pháp:
Áp dụng quy tắc: Muốn rút gọn phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác \(1\) và \( - 1\)) của chúng.
Cách giải:
a) \(\frac{{ - 16}}{{72}} = \frac{{ - 16:8}}{{72:8}} = \frac{{ - 2}}{9}\)
b)\(\frac{{4.15}}{{3.12}} = \frac{{4.3.5}}{{3.4.3}} = \frac{{12.5}}{{12.3}} = \frac{5}{3}\)
Câu 3 (NB)
Phương pháp:
Áp dụng các quy tắc phép cộng phân số.
Cách giải:
a)
\(\begin{array}{l}\frac{{ - 9}}{{15}} + \frac{{ - 6}}{{15}} = \frac{{\left( { - 9} \right) + \left( { - 6} \right)}}{{15}}\\ = \frac{{ - 15}}{{15}} = - 1\end{array}\)
b)
\(\begin{array}{l}\frac{{15}}{{20}} + \frac{7}{4} = \frac{{15}}{{20}} + \frac{{35}}{{20}}\\ = \frac{{15 + 35}}{{20}} = \frac{{50}}{{20}} = \frac{5}{2}\end{array}\)
c)
\(\begin{array}{l}\frac{{ - 4}}{{16}} + \frac{{ - 3}}{8} = \frac{{ - 4}}{{16}} + \frac{{ - 6}}{{16}}\\ = \frac{{\left( { - 4} \right) + \left( { - 6} \right)}}{{16}} = \frac{{ - 10}}{{16}} = \frac{{ - 5}}{8}\end{array}\)
d)
\(\begin{array}{l}\frac{2}{{12}} + \frac{7}{{24}} = \frac{4}{{24}} + \frac{7}{{24}}\\ = \frac{{4 + 7}}{{24}} = \frac{{11}}{{24}}\end{array}\)
Câu 4 (VD)
Phương pháp:
Giải bài toán ngược để tìm \(x\).
Cách giải:
a) \(5 - 2x = - 21\)
\(\begin{array}{l}5 - 2x = - 21\\ - 2x = - 5 - 21\\ - 2x = - 26\\x = \left( { - 26} \right):\left( { - 2} \right)\\x = 13\end{array}\)
Vậy \(x = 13\).
b) \(\frac{{ - 3}}{x} = \frac{3}{5} + \frac{{ - 9}}{{20}}\)
\(\begin{array}{l}\frac{{ - 3}}{x} = \frac{3}{5} + \frac{{ - 9}}{{20}}\\\frac{{ - 3}}{x} = \frac{{12}}{{20}} + \frac{{ - 9}}{{20}}\\\frac{{ - 3}}{x} = \frac{3}{{20}}\\\frac{3}{{ - x}} = \frac{3}{{20}}\\ - x = 20\\x = - 20\end{array}\)
Vậy \(x = - 20\).
Câu 5 (VD)
Phương pháp:
a) Áp dụng dấu hiệu nhận biết tia nằm giữa hai tia.
b) Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì\(\angle xOy + \angle yOz = \angle xOz\).
c) \(Om\) là tia phân giác của góc \(\angle xOy\) nếu thỏa mãn điều kiện sau:
+ Tia \(Om\) nằm giữa hai tia \(Ox\) và \(Oy\)
+ \(\angle xOm = \angle mOy\)
d) Áp dụng lý thuyết về hai tia đối nhau, hai góc kề bù.
Cách giải:
Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\), vẽ hai tia \(Oy\) và \(Oz\) sao cho \(\angle xOy = {128^0}\), \(\angle xOz = {64^0}\).
a) Trong ba tia \(Ox,\,\,Oy,\,\,Oz\) thì tia nào nằm giữa hai tia còn lại?
Trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\), có \(\angle xOz < \angle xOy\) (vì \({64^0} < {128^0}\)) nên tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\).
b) Tính số đo \(\angle yOz\).
Vì tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\) nên ta có:
\(\angle xOz + \angle yOz = \angle xOy\)
\(\angle yOz = \angle xOy - \angle xOz\)
\(\angle yOz = {128^0} - {64^0}\)
\(\angle yOz = {64^0}\)
Vậy \(\angle yOz = {64^0}\).
c) Tia \(Oz\) có phải là tia phân giác của góc \(xOy\) không? Vì sao?
Ta có:
+ Tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\)(theo câu a)
+ \(\angle xOz = \angle yOz\left( { = {{64}^0}} \right)\)(theo câu b)
\( \Rightarrow \) Tia \(Oz\) là tia phân giác của góc \(xOy\) (định nghĩa)
d) Gọi \(Ot\) là tia đối của tia \(Oy\). Tính số đo \(\angle xOt\).
Vì \(Oy\) và \(Ot\) là hai tia đối nhau nên \(\angle xOy\) và \(\angle xOt\)là hai góc kề bù. Khi đó, ta có:
\(\angle xOy + \angle xOt = {180^0}\)
\(\angle xOt = {180^0} - \angle xOy\)
\(\angle xOt = {180^0} - {128^0}\)
\(\angle xOt\, = {52^0}\)
Vậy \(\angle xOt = {52^0}\).
Các bài khác cùng chuyên mục













Danh sách bình luận