-
Toán 9 tập 1 - Cùng khám phá
-
Toán 9 tập 2 - Cùng khám phá
Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá
Bài 1. Các tỉ số lượng giác của góc nhọn - Toán 9 Cùng ..
Lý thuyết Các tỉ số lượng giác của góc nhọn Toán 9 Cùng khám phá
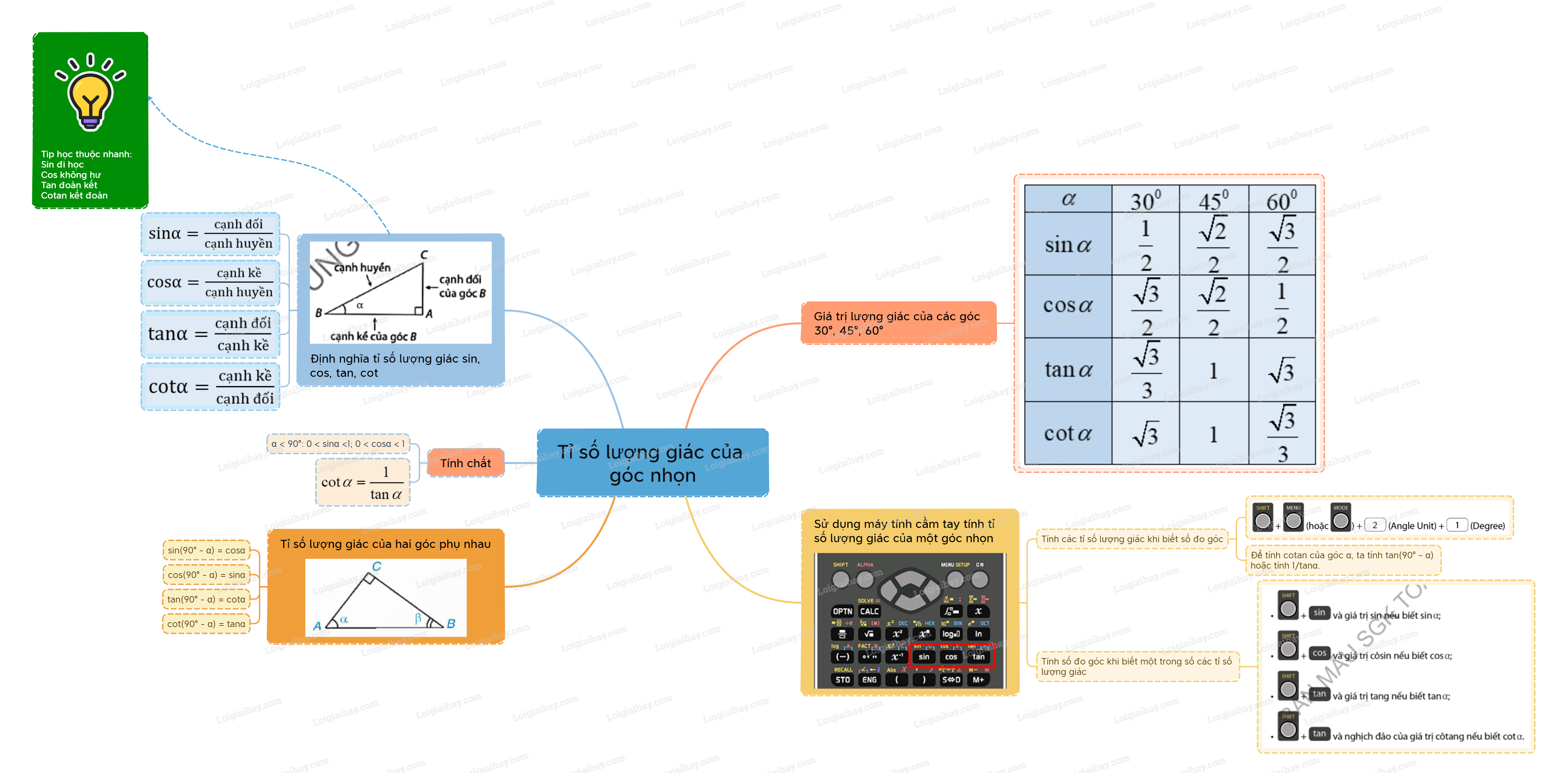
1. Khái niệm tỉ số lượng giác của một góc nhọn \({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}};{\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}};\) \({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}};{\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\) \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) gọi là các tỉ số lượng giác của góc nhọn \(\alpha \).
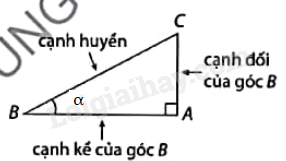
1. Khái niệm tỉ số lượng giác của một góc nhọn
|
\({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}};{\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}};\) \({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}};{\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\) \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) gọi là các tỉ số lượng giác của góc nhọn \(\alpha \). |
Tip học thuộc nhanh:
|
Sin đi học Cos không hư Tan đoàn kết Cotang kết đoàn |
Lưu ý:
1. Trong một tam giác vuông, độ dài các cạnh luôn là số dương và cạnh góc vuông luôn nhỏ hơn cạnh huyền. Do đó sin và côsin của một góc nhọn luôn dương và nhỏ hơn 1.
\(\alpha < {90^0}:0 < \sin \alpha < 1;0 < \cos \alpha < 1\).
2. Khi ghi các tỉ số lượng giác của một góc nhọn trong tam giác, ta viết \(\sin A\) thay vì \(\sin \widehat A\).
3. \(\cot \alpha = \frac{1}{{\tan \alpha }}\).
Ví dụ:
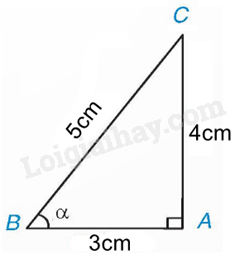
Theo định nghĩa của tỉ số lượng giác, ta có:
\(\sin \alpha = \frac{{AC}}{{BC}} = \frac{4}{5}\), \(\cos \alpha = \frac{{AB}}{{BC}} = \frac{3}{5}\), \(\tan \alpha = \frac{{AC}}{{AB}} = \frac{4}{3}\), \(\cot \alpha = \frac{{AB}}{{AC}} = \frac{3}{4}\)
2. Tỉ số lượng giác của một số góc đặc biệt
Bảng giá trị lượng giác của các góc \({30^0},{45^0},{60^0}\)
|
\(\alpha \) |
\({30^0}\) |
\({45^0}\) |
\({60^0}\) |
|
\(\sin \alpha \) |
\(\frac{1}{2}\) |
\(\frac{{\sqrt 2 }}{2}\) |
\(\frac{{\sqrt 3 }}{2}\) |
|
\(\cos \alpha \) |
\(\frac{{\sqrt 3 }}{2}\) |
\(\frac{{\sqrt 2 }}{2}\) |
\(\frac{1}{2}\) |
|
\(\tan \alpha \) |
\(\frac{{\sqrt 3 }}{3}\) |
\(1\) |
\(\sqrt 3 \) |
|
\(\cot \alpha \) |
\(\sqrt 3 \) |
\(1\) |
\(\frac{{\sqrt 3 }}{3}\) |
3. Tỉ số lượng giác của hai góc phụ nhau
Định lí về tỉ số lượng giác của hai góc phụ nhau
|
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtang góc kia. \(\begin{array}{l}\sin \alpha = \cos \left( {{{90}^0} - \alpha } \right);\cos \alpha = \sin \left( {{{90}^0} - \alpha } \right);\\\tan \alpha = \cot \left( {{{90}^0} - \alpha } \right);\cot \alpha = \tan \left( {{{90}^0} - \alpha .} \right)\end{array}\) |
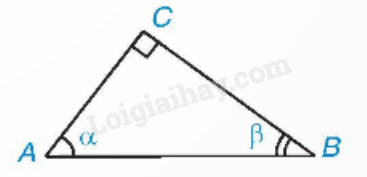
Cho \(\alpha \) và \(\beta \) là hai góc phụ nhau, ta có:
\(\sin \alpha = \cos \beta \), \(\cos \alpha = \sin \beta \), \(\tan \alpha = \cot \beta \), \(\cot \alpha = \tan \beta \).
Ví dụ:
\(\begin{array}{l}\sin {60^0} = \cos \left( {{{90}^0} - {{60}^0}} \right) = \cos {30^0};\\\cos {52^0}30' = \sin \left( {{{90}^0} - {{52}^0}30'} \right) = \sin {37^0}30';\\\tan {80^0} = \cot \left( {{{90}^0} - {{80}^0}} \right) = \cot {10^0};\\\cot {82^0} = \tan \left( {{{90}^0} - {{82}^0}} \right) = \tan {8^0}.\end{array}\)
4. Tính các tỉ số lượng giác của một góc khi biết số đo góc và tính số đo góc khi biết tỉ số lượng giác bằng máy tính cầm tay.
a) Tính tỉ số lượng giác khi biết số đo góc
Ngoài đơn vị độ, người ta còn dùng đơn vị phút (‘) và giây (“) để đo góc chính xác hơn với \({1^0} = 60';1' = 60''\).
Để tính các tỉ số lượng giác sin, côsin và tang của một góc, ta sử dụng các phím
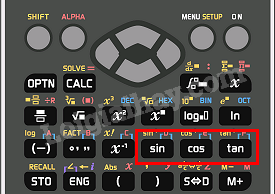
Để tính giá trị côtang của một góc \(\alpha \), ta tính tang của \({90^0} - \alpha \) hoặc tính giá trị \(\frac{1}{{\tan \alpha }}\).
b) Tìm số đo góc khi biết tỉ số lượng giác
Khi biết tỉ số lượng giác của một góc nhọn, ta cũng có thể sử dụng máy tính cầm tay để tính số đo của góc nhọn đó. Để tìm góc nhọn \(\alpha \), ta bấm:
Một số công thức mở rộng:
+) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
+) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\)
+) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\)
+) \(\tan \alpha .\cot \alpha = 1\)
+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\)
+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha + 1\)
Bình luận
Chia sẻ
- Giải câu hỏi khởi động trang 75 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 1 trang 75, 76 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 2 trang 76, 77 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 3 trang 78 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 4 trang 79, 80, 81 SGK Toán 9 tập 1 - Cùng khám phá
>> Xem thêm
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
