Giải mục 3 trang 78 SGK Toán 9 tập 1 - Cùng khám phá

Cho tam giác ABC vuông tại A (Hình 4.10). a) Tổng số đo của góc B và góc C bằng bao nhiêu độ? b) Viết các tỉ số lượng giác của góc B và góc C, từ đó chỉ ra các cặp tỉ số lượng giác bằng nhau.

Lựa chọn câu để xem lời giải nhanh hơn

HĐ4
LT3

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 78 SGK Toán 9 Cùng khám phá

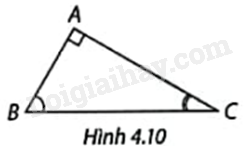
Cho tam giác ABC vuông tại A (Hình 4.10).

a) Tổng số đo của góc B và góc C bằng bao nhiêu độ?

b) Viết các tỉ số lượng giác của góc B và góc C, từ đó chỉ ra các cặp tỉ số lượng giác bằng nhau.

Phương pháp giải:

a) Tam giác ABC vuông tại A nên \(\widehat B + \widehat C = {90^o}\).

b) Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).

Lời giải chi tiết:

a) Tam giác ABC vuông tại A nên \(\widehat B + \widehat C = {90^o}\).

b) Tam giác ABC vuông tại A nên:

+) \(\sin B = \frac{{CA}}{{BC}}\), \(\cos B = \frac{{BA}}{{BC}}\), \(\tan B = \frac{{CA}}{{AB}}\), \(\cot B = \frac{{AB}}{{AC}}\).

+) \(\cos C = \frac{{CA}}{{BC}}\), \(\sin C = \frac{{BA}}{{BC}}\), \(\cot C = \frac{{CA}}{{AB}}\), \(\tan C = \frac{{AB}}{{AC}}\).

Do đó, \(\sin B = \cos C\), \(\cos B = \sin B\), \(\tan B = \cot C\), \(\cot B = \tan C\).

LT3

Trả lời câu hỏi Luyện tập 3 trang 78 SGK Toán 9 Cùng khám phá

Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc lớn hơn \({45^o}\):

a) \(\cos {25^o}\);

b) \(\cot {31^o}\).

Phương pháp giải:

Sử dụng kiến thức:

\(\cos \alpha = \left( {{{90}^o} - \alpha } \right),\cot \alpha = \tan \left( {{{90}^o} - \alpha } \right)\)

Lời giải chi tiết:

a) \(\cos {25^o} = \sin \left( {{{90}^o} - {{25}^o}} \right) = \sin {65^o}\);

b) \(\cot {31^o} = \tan \left( {{{90}^o} - {{31}^o}} \right) = \tan {59^o}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 4 trang 79, 80, 81 SGK Toán 9 tập 1 - Cùng khám phá
Sử dụng máy tính cầm tay, hãy tính \(\cos {13^o}\) và \(\tan {71^o}25'\). Làm tròn kết quả đến hàng phần trăm.
Giải bài tập 4.1 trang 82 SGK Toán 9 tập 1 - Cùng khám phá
Tính tỉ số lượng giác của các góc \(\alpha \) và \(\beta \) trong mỗi trường hợp ở Hình 4.13.
Giải bài tập 4.2 trang 82 SGK Toán 9 tập 1 - Cùng khám phá
Sử dụng máy tính cầm tay, hãy tính và sắp xếp các tỉ số lượng giác sau theo thứ tự từ nhỏ đến lớn: a) \(\sin {56^o},\sin {10^o},\sin {48^o},\sin {14^o}\); b) \(\cos {78^o},\cos {38^o},\cos {13^o},\cos {83^o}\).
Giải bài tập 4.3 trang 82 SGK Toán 9 tập 1 - Cùng khám phá
Cho hình chữ nhật ABCD có \(\widehat {ABD} = 2\widehat {CBD}\). Hãy tính tỉ số chiều dài và chiều rộng của hình chữ nhật ABCD.
Giải bài tập 4.4 trang 82 SGK Toán 9 tập 1 - Cùng khám phá
Khi một vật được ném xiên một góc \(\alpha \) so với mặt đất và tốc độ ném ban đầu là \({v_o}\left( {m/s} \right)\) (Hình 4.14), độ cao lớn nhất H(m) mà vật có thể đạt đến được cho bởi công thức: \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) (nguồn: https://phys.libretexts.org/Bookshelves/University_Physics/Physics_(Boundless)/3%3A_Two-Dimensional_Kinematics/3.3%3A_Projectile_Motion). Tính độ cao lớn nhất của vật nếu tốc độ ném ban đầu là 12m/s và góc ném là: a) \({45^o}\); b
Giải bài tập 4.5 trang 82 SGK Toán 9 tập 1 - Cùng khám phá
Sử dụng máy tính cầm tay, tính số đo góc nhọn \(\alpha \), biết: a) \(\sin \alpha = 0,3\); b) \(\cos \alpha = \frac{1}{2}\); c) \(\tan \alpha = \frac{5}{7}\); d) \(\cot \alpha = 4\). Làm tròn số đo góc đến phút.
Giải bài tập 4.6 trang 82 SGK Toán 9 tập 1 - Cùng khám phá
Tính số đo các góc nhọn của các tam giác vuông ở Hình 4.15. Làm tròn số đo góc đến độ.
Giải mục 2 trang 76, 77 SGK Toán 9 tập 1 - Cùng khám phá
Trong Hình 4.6, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B.
Giải mục 1 trang 75, 76 SGK Toán 9 tập 1 - Cùng khám phá
1. Vẽ một góc nhọn có số đo (alpha ) bất kì. Chọn một điểm C trên một cạnh và vẽ đường vuông góc CA từ C xuống cạnh còn lại (Hình 4.3). Hãy đo và tính các tỉ số cạnh đối và cạnh huyền, cạnh kề và cạnh huyền, cạnh đối và cạnh kề của góc B trong tam giác ABC. 2. Vẽ thêm một góc nhọn B’ cũng có số đo (alpha ) như trên và thực hiện tương tự. 3. Sử dụng dấu hiệu đồng dạng của hai tam giác vuông, hãy giải thích vì sao các cặp tỉ số tương ứng của (widehat B) và (widehat {B'}) bằng nhau.
Giải câu hỏi khởi động trang 75 SGK Toán 9 tập 1 - Cùng khám phá
Theo quy chuẩn kĩ thuật quốc gia về xây dựng công trình đảm bảo cho người khuyết tật tiếp cận sử dụng (QCVN 10:2014/BXD), tỉ số giữa chiều cao h và chiều dài theo phương ngang d của dốc cho xe lăn không được lớn hơn \(\frac{1}{{12}}\) như Hình 4.1. Nếu góc nghiêng của một con dốc so với phương ngang là \(\alpha = {5^o}\) thì con dốc đó có đáp ứng được quy chuẩn trên không?
Lý thuyết Các tỉ số lượng giác của góc nhọn Toán 9 Cùng khám phá
1. Khái niệm tỉ số lượng giác của một góc nhọn \({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}};{\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}};\) \({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}};{\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\) \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) gọi là các tỉ số lượng giác của góc nhọn \(\alpha \).