Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá

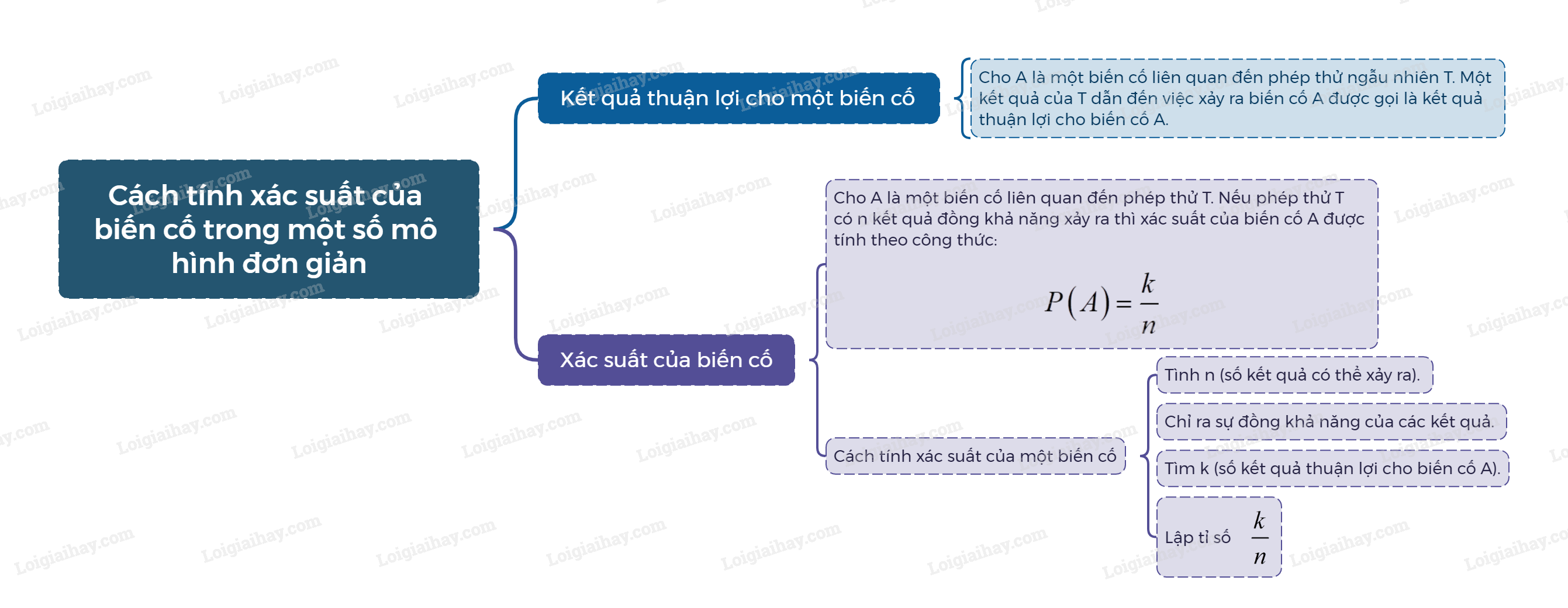
1. Kết quả thuận lợi cho một biến cố Cho A là một biến cố liên quan đến phép thử ngẫu nhiên T. Một kết quả của T dẫn đến việc xảy ra biến cố A được gọi là kết quả thuận lợi cho biến cố A.

1. Kết quả thuận lợi cho một biến cố

Cho A là một biến cố liên quan đến phép thử ngẫu nhiên T. Một kết quả của T dẫn đến việc xảy ra biến cố A được gọi là kết quả thuận lợi cho biến cố A.

Ví dụ: Bạn Lan gieo một con xúc xắc và bạn Hòa gieo một đồng xu được gọi là phép thử.

Kết quả của phép thử là số chấm xuất hiện trên con xúc xác và mặt xuất hiện của đồng xu.

Các kết quả có thể của phép thử là:

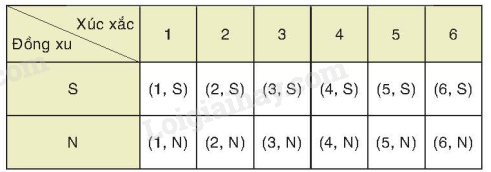
Các kết quả thuận lợi cho biến cố “Số chấm xuất hiện trên con xúc xắc là số chẵn và mặt xuất hiện của đồng xu là mặt sấp” là (2, S); (4, S); (6, S).

2. Tính xác suất của biến cố

Cho A là một biến cố liên quan đến phép thử T. Nếu phép thử T có n kết quả đồng khả năng xảy ra thì xác suất của biến cố A được tính theo công thức:

\(P\left( A \right) = \frac{k}{n}\).

Cách tính xác suất của một biến cố

Để tính xác suất của biến cố A, ta có thể thực hiện các bước sau:

Bước 1: Tình n (số kết quả có thể xảy ra).

Bước 2: Chỉ ra sự đồng khả năng của các kết quả.

Bước 3: Tìm k (số kết quả thuận lợi cho biến cố A).

Bước 4: Lập tỉ số \(\frac{k}{n}\).

Ví dụ: Ba bạn Bảo, Châu, Dương được xếp ngẫu nhiên ngồi trên một hàng ghế có ba chỗ ngồi. Tính xác suất của các biến cố sau:

a) E: "Bảo không ngồi ngoài cùng bên phải";

b) F: “Châu và Dương không ngồi cạnh nhau”.

Lời giải:

Kí hiệu ba bạn Bảo, Châu, Dương lần lượt là B, C, D.

Vì việc xếp chỗ ngồi là ngẫu nhiên nên các kết quả có thể là đồng khả năng.

Ta liệt kê các kết quả có thể xảy ra:

• Bảo ngồi ngoài cùng bên trái: có 2 cách xếp là BCD và BDC.

• Bảo ngồi giữa: có 2 cách xếp là CBD và DBC.

• Bảo ngồi ngoài cùng bên phải: có 2 cách xếp là CDB và DCB.

Vậy không gian mẫu của phép thử là \(\Omega = \left\{ {BCD;{\rm{ }}BDC;{\rm{ }}CBD;{\rm{ }}DBC;{\rm{ }}CDB;{\rm{ }}DCB} \right\}.\)

Tập \(\Omega \) có 6 phần tử.

a) Có 4 kết quả thuận lợi cho biến cố E là BCD, BDC, CBD và DBC.

Vậy \(P\left( E \right) = \frac{4}{6} = \frac{2}{3}\).

b) Có 2 kết quả thuận lợi cho biến cố F là CBD và DBC.

Vậy \(P\left( F \right) = \frac{2}{6} = \frac{1}{3}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 125, 126 SGK Toán 9 tập 2 - Cùng khám phá
Xét trò chơi “rút thẻ” nó trên. Gọi A là biến cố “Bạn Trung được 1 điểm thưởng”. Trong mỗi lần bạn Trung rút thẻ, có những kết quả nào dẫn đến việc biến cố A xảy ra? Trò chơi “rút thẻ” : Trong hộp có 10 thẻ giống hệt nhau. Trên mỗi thẻ có ghi một trong các số từ 1 đến 10 (không có thẻ nào trùng số). Bạn Trung rút ngẫu nhiên một thẻ, xác định số ghi trên thẻ rồi bỏ lại vào hộp. Nếu lấy được thẻ có ghi một số chia hết cho 3 thì Trung được 1 điểm thưởng và có quyền rút thẻ lần nữa. Nếu rút được th
Giải mục 2 trang 127, 128, 129 SGK Toán 9 tập 2 - Cùng khám phá
Bạn Mai tạo danh sách gồm những bài hát mình yêu thích trên một ứng dụng nghe nhạc. Danh sách của Mai gồm 7 bài hát tiếng Việt, 4 bài hát tiếng Anh, 6 bài hát tiếng Pháp. Mỗi lần nghe nhạc, Mai mở danh sách và chọn chế độ phát ngẫu nhiên. Theo chế độ này, ứng dụng nghe nhạc sẽ bắt đầu từ một bài chọn ngẫu nhiên trong danh sách. a) Xác định không gian mẫu của phép thử chọn ngẫu nhiên một bài hát. b) Khả năng mỗi bài được chọn có như nhau không? c) Liệt kê các kết quả thuận lợi cho biến cố A: “
Giải bài tập 10.20 trang 130 SGK Toán 9 tập 2 - Cùng khám phá
Phân xưởng H của nhà máy có 2 kĩ sư, 25 kĩ thuật viên và 7 thợ học việc. Người ta chọn ngẫu nhiên một người trong số này để phỏng vấn về chế độ đãi ngộ của nhà máy. Hãy tính xác suất của các biến cố: a) Chọn được một thợ học việc; b) Chọn được một kĩ sư hoặc kĩ thuật viên.
Giải bài tập 10.21 trang 130 SGK Toán 9 tập 2 - Cùng khám phá
Tung hai lần con xúc xắc bốn mặt được đánh số 1, 2, 3, 4 và tính tổng của hai số được ghi trên mặt úp xuống. Tìm xác suất của biến cố: a) A: “Tổng hai số bằng 5”; b) B: “Tổng hai số không phải là ước của 8”.
Giải bài tập 10.22 trang 130 SGK Toán 9 tập 2 - Cùng khám phá
Nhà máy kiểm tra chất lượng sản phẩm do hai dây chuyền Y, Z sản xuất và thống kê số sản phẩm đạt, không đạt chất lượng trong bảng sau: Lấy ngẫu nhiên một sản phẩm trong số những sản phẩm này. Tính xác suất của biến cố: a) C: “Lấy được một phế phẩm (sản phẩm không đạt chất lượng)”; b) D: “Lấy được một sản phẩm đạt chất lượng do dây chuyền Z sản xuất”; c) E: “Lấy được một sản phẩm do dây chuyền Y sản xuất”.
Giải bài tập 10.23 trang 130 SGK Toán 9 tập 2 - Cùng khám phá
Trong hộp các chữ cái vừa đủ để xếp thành từ CÙNG KHÁM PHÁ. Lấy ngẫu nhiên một chữ cái trong hộp. Tìm xác suất của biến cố A: “Lấy được một phụ âm”.
Giải bài tập 10.24 trang 130 SGK Toán 9 tập 2 - Cùng khám phá
Phòng thí nghiệm của một nhà máy sản xuất bóng đèn thông báo: Trong số những bóng đèn sợi đốt đã kiểm tra, 26% bóng có tuổi thọ tối thiểu 1200 giờ, còn lại là số bóng đạt tuổi thọ dưới 1200 giờ. Hỏi xác suất để một khách hàng mua được một bóng đèn có tuổi thọ tuối thiểu 1200 giờ là bao nhiêu?
Giải bài tập 10.25 trang 130 SGK Toán 9 tập 2 - Cùng khám phá
Một hộp đựng 20 viên bi đỏ và xanh có cùng kích thước, khối lượng. Tìm số viên bi mỗi màu, biết rằng xác suất của biến cố A: “Lấy được viên bi đỏ” khi thực hiện phép thử lấy ngẫu nhiên một viên bi là P(A) = 0,6.