Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá Bài 5. Phép thử ngẫu nhiên. Không gian mẫu - Toán 9 Cùn..

Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá


1. Phép thử ngẫu nhiên Một thí nghiệm, một hành động được gọi là phép thử ngẫu nhiên (gọi tắt là phép thử) nếu ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể xảy ra. Nhận xét: Các phép thử ngẫu nhiên có thể được lặp lại nhiều lần, và dù lặp lại trong những điều kiện giống hệt nhau thì cũng không chắc là sẽ cho cùng kết quả.

1. Phép thử ngẫu nhiên

Một thí nghiệm, một hành động được gọi là phép thử ngẫu nhiên (gọi tắt là phép thử) nếu ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể xảy ra.

Nhận xét:

Các phép thử ngẫu nhiên có thể được lặp lại nhiều lần, và dù lặp lại trong những điều kiện giống hệt nhau thì cũng không chắc là sẽ cho cùng kết quả.

2. Không gian mẫu

Tập hợp các kết quả có thể xảy ra của một phép thử được gọi là không gian mẫu của phép thử đó và kí hiệu là \(\Omega \).

Tổng số kết quả có thể xảy ra gọi là số kết quả (hay số phần tử) của không gian mẫu.

Ví dụ: Bạn Lan gieo một con xúc xắc và bạn Hòa gieo một đồng xu được gọi là phép thử.

Kết quả của phép thử là số chấm xuất hiện trên con xúc xác và mặt xuất hiện của đồng xu.

Các kết quả có thể của phép thử là:

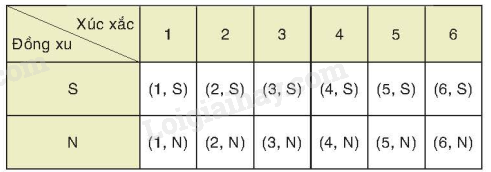
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 12 ô của bảng trên.

Do đó không gian mẫu của phép thử là:

\(\Omega  = {\rm{\{ (1,S);(2,S);(3,S);(4,S);(5,S);(6,S);(1,N);(2,N);(3,N);(4,N);(5,N);(6,N)\} }}{\rm{.}}\)

Vậy không gian mẫu có 12 phần tử.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 1 trang 121, 122 SGK Toán 9 tập 2 - Cùng khám phá

    a) Khi tung một con xúc xắc có 6 mặt, ta có biết trước là chắc chắn sẽ nhận được mặt 6 chấm không? b) Trong hộp có 6 viên bi vàng, 1 viên bi đỏ giống hệt nhau về kích thước, khối lượng. Không nhìn vào hộp và lấy ngẫu nhiên 1 viên bi. Trước khi lấy, ta có chắc chắn sẽ được viên bi đỏ không? Nếu lần thứ nhất lấy được viên bi đỏ, bỏ lại viên bi vào hộp, trộn đều, rồi lấy lần thứ hai thì có chắc là lần thứ hai cũng lấy được viên bi đỏ không?

  • Giải mục 2 trang 122, 123, 124 SGK Toán 9 tập 2 - Cùng khám phá

    Trong hộp có 4 thẻ màu đỏ được đánh số 1, 2, 3, 4 và 3 thẻ màu xanh được đánh số 1, 2, 3. Lấy ngẫu nhiên một thẻ trong hộp. Hãy liệt kê các kết quả có thể xảy ra khi thực hiện hành động này. Có bao nhiêu kết quả có thể xảy ra?

  • Giải bài tập 10.16 trang 124 SGK Toán 9 tập 2 - Cùng khám phá

    Trong các hành động dưới đây, hành động nào là phép thử ngẫu nhiên? Giải thích vì sao. a) Lấy một viên bi bất kì trong hộp kín đựng những viên bi có màu khác nhau; b) Tìm kết quả của một dãy phép tính. c) Lấy trên giá của siêu thị một chùm nho, cân và ghi lại khối lượng của nó.

  • Giải bài tập 10.17 trang 124 SGK Toán 9 tập 2 - Cùng khám phá

    Xét phép thử quay bánh xe ở hình dưới để quan sát xem khi bánh xe dừng ở mũi kim (được gắn cố định) chỉ vào ô ghi số mấy. Hãy liệt kê các phần tử của không gian mẫu.

  • Giải bài tập 10.18 trang 124 SGK Toán 9 tập 2 - Cùng khám phá

    Trong một bể cá có 15 con gồm ba màu đỏ, trắng và vàng. Số cá màu đỏ gấp hai lần số cá màu vàng. Số cá màu vàng nhiều hơn 1 con so với số cá màu trắng. Bắt một con các bất kì trong bể. Hãy liệt kê các phần tử của không gian mẫu của phép thử bắt cá.

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store