 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 1. Vectơ và các phép toán trong không gian - Toán 1..
Bài 1. Vectơ và các phép toán trong không gian - Toán 1..
Giải mục 2 trang 43, 44, 45, 46 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng và hiệu của hai vectơ
KP2
Trả lời câu hỏi Khám phá 2 trang 43 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.A′B′C′D′ (Hình 5).
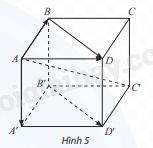
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow {AB} + \overrightarrow {BC} \).
b) So sánh hai vectơ \(\overrightarrow {BD'} ,\overrightarrow {B'D'} \).
c) Giải thích tại sao \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AD} \).
Phương pháp giải:
Áp dụng quy tắc hình bình hành và quy tắc ba điểm.
Lời giải chi tiết:
a) \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
b) \(\overrightarrow {BD'} = \overrightarrow {B'D'} \).
c) \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \).
KP3
Trả lời câu hỏi Khám phá 3 trang 44 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.A′B′C′D′.
a) Tìm các vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AD} \), \(\overrightarrow {AC} + \overrightarrow {AA'} \).
b) Dùng kết quả của câu a và tính chất kết hợp của phép cộng vectơ để chứng minh \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Phương pháp giải:
Áp dụng quy tắc hình bình hành và tính chất kết hợp của phép cộng.
Lời giải chi tiết:
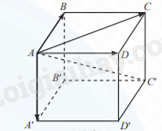
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);\(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
b) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
TH3
Trả lời câu hỏi Thực hành 3 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.EFGH. Tìm các vecto:
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} \).
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} \).
Phương pháp giải:
Áp dụng quy tắc hình bình hành, hình hộp và 2 vecto bằng nhau.
Lời giải chi tiết:
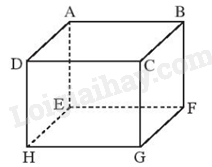
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} = \overrightarrow {DB} + \overrightarrow {DH} = \overrightarrow {DF} \).
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} = \overrightarrow {HE} + \overrightarrow {HD} + \overrightarrow {HG} = \overrightarrow {HB} \).
KP4
Trả lời câu hỏi Khám phá 4 trang 45 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp $ABCD, A'B'C'D'$.
a) Trong mặt phẳng ($ABCD$), tìm vectơ hiệu $\overrightarrow{AB} - \overrightarrow{AD}$. Trong mặt phẳng ($A'B'C'D'$), tìm vectơ hiệu $\overrightarrow{A'B'} - \overrightarrow{A'D'}$.
b) Tìm mối liên hệ giữa các cặp vectơ $\overrightarrow{AB}$ và $\overrightarrow{A'B'}$, $\overrightarrow{AD}$ và $\overrightarrow{A'D'}$, $\overrightarrow{DB}$ và $\overrightarrow{D'B'}$.
c) Giải thích tại sao $\overrightarrow{AB} - \overrightarrow{AD} = \overrightarrow{A'B'} - \overrightarrow{A'D'}$.
Phương pháp giải:
Áp dụng quy tắc hiệu và 2 vecto bằng nhau.
Lời giải chi tiết:

a) Áp dụng quy tắc hiệu:
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \), \(\overrightarrow {A'B'} - \overrightarrow {A'D'} = \overrightarrow {D'B'} \).
b) \(\overrightarrow {AB} = \overrightarrow {A'B'} \), \(\overrightarrow {AD} = \overrightarrow {A'D'} \), \(\overrightarrow {DB} = \overrightarrow {D'B'} \).
c) Vì \(\overrightarrow {DB} = \overrightarrow {D'B'} \) nên \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {A'B'} - \overrightarrow {A'D'} \).
TH4
Trả lời câu hỏi Thực hành 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Hãy thực hiện các phép toán sau đây:
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} \).
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} \).
Phương pháp giải:
Áp dụng quy tắc ba điểm, quy tắc hiệu và tính chất trung điểm.
Lời giải chi tiết:
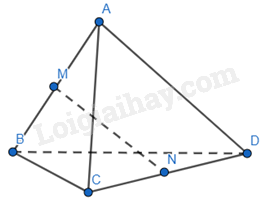
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} \)
\(= \overrightarrow {MC} + \overrightarrow {CN} = \overrightarrow {MN} \).
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {MA} + \overrightarrow {DN} \)
\(= \overrightarrow {MD} + \overrightarrow {DN} = \overrightarrow {MN} \).
TH5
Trả lời câu hỏi Thực hành 5 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình lập phương ABCD. A′B′C′D′ có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) \(\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} \).
b) \(\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp và định lí Pytago.
Lời giải chi tiết:
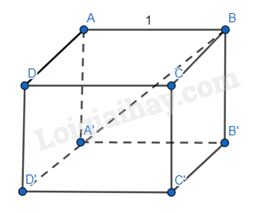
a) \(\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
\(|\overrightarrow a | = |\overrightarrow {BD'} | = \sqrt {B{D^2} + D{D^2}} \)
\(= \sqrt {B{A^2} + B{C^2} + D{D^2}} = \sqrt {1 + 1 + 1} = \sqrt 3 \).
b) \(\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A}\)
\( = \overrightarrow {BC} + \overrightarrow {AB} + \overrightarrow {C'A} = \overrightarrow {CC'} \).
\(|\overrightarrow b | = |\overrightarrow {CC'} | = 1\).
VD2
Trả lời câu hỏi Vận dụng 2 trang 46 SGK Toán 12 Chân trời sáng tạo
Ba lực \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2N; 3N; 4N (Hình 17). Tính độ lớn hợp lực của ba lực đã cho.

Phương pháp giải:
Áp dụng quy tắc hình bình hành và định lí Pytago.
Lời giải chi tiết:
Ta có: \(|\overrightarrow {{F_2}} + \overrightarrow {{F_3}} | = \sqrt {{F_2}^2 + {F_3}^2} = \sqrt {{3^2} + {4^2}} = 5\).
Độ lớn hợp lực của ba lực là: \(|\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} | = \sqrt {{F_1}^2 + {5^2}} = \sqrt {{2^2} + {5^2}} = \sqrt {29} \) N.
- Giải mục 3 trang 46, 47, 48 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải mục 4 trang 48, 49, 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 2 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận