Giải mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo

Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác (frac{{2pi

Tổng hợp đề thi giữa kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1
TH1

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 13 SGK Toán 11 Chân trời sáng tạo

Trong Hình 1, M và N lần lượt là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{-\pi }{4}\) trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.

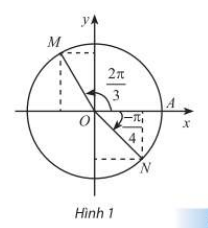
Phương pháp giải:

Dựa vào kiến thức đã học để xác định.

Lời giải chi tiết:

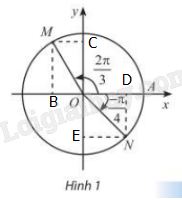
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy.

D,E lần lượt là hình chiếu của N lên Ox, Oy.

Ta có OM = ON = 1.

\(\widehat {MOC} = \frac{{2\pi }}{3} - \frac{\pi }{2} = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {MOC} = \frac{1}{2} = \frac{{MC}}{{OM}} \Rightarrow MC = \frac{1}{2}\\\cos \widehat {MOC} = \frac{{\sqrt 3 }}{2} = \frac{{MB}}{{OM}} \Rightarrow MB = \frac{{\sqrt 3 }}{2}\end{array} \right.\)

Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M \(\left( {\frac{-1}{2};\frac{{\sqrt 3 }}{2}} \right)\)

\(\widehat {NOD} = - \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {NOD} = - \frac{{\sqrt 2 }}{2} = \frac{{ND}}{{ON}} \Rightarrow ND = - \frac{{\sqrt 2 }}{2}\\\cos \widehat {NOD} = \frac{{\sqrt 2 }}{2} = \frac{{NE}}{{ON}} \Rightarrow NE = \frac{{\sqrt 2 }}{2}\end{array} \right.\)

Tọa độ của điểm N \(\left( { \frac{{\sqrt 2 }}{2};\frac{-{\sqrt 2 }}{2}} \right)\).

TH1

Trả lời câu hỏi Thực hành 1 trang 15 SGK Toán 11 Chân trời sáng tạo

Tính \(\sin \left( { - \frac{{2\pi }}{3}} \right)\) và \(\tan 495^\circ \).

Phương pháp giải:

Dựa vào kiến thức đã học ở phần trên để tính.

Lời giải chi tiết:

\(\begin{array}{l}\sin \left( { - \frac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2};\\\tan 495^\circ = - 1.\end{array}\)

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Giải mục 2 trang 16 SGK Toán 11 tập 1 - Chân trời sáng tạo
Sử dụng máy tính cầm tay để tính (cos 75^circ ) và (tan left( { - frac{{19pi }}{6}} right))
Giải mục 3 trang 16, 17 SGK Toán 11 tập 1 - Chân trời sáng tạo
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao ({sin ^2}alpha + {cos ^2}alpha = 1)
Giải mục 4 trang 17, 18, 19 GK Toán 11 tập 1 - Chân trời sáng tạo
Cho (alpha = frac{pi }{3}). Biểu diễn các góc lượng giác ( - alpha ,alpha + pi ,pi - alpha ,frac{pi }{2} - alpha ) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc (alpha )
Bài 1 trang 19 SGK Toán 11 tập 1 - Chân trời ság tạo
Các đẳng thức sau có thể đồng thời xảy ra không?
Bài 2 trang 19 SGK Toán 11 tập 1 - Chân trời ság tạo
Cho \(\cos \alpha = - \frac{5}{{13}}\). Tính \(\sin \left( { - \frac{{15\pi }}{2} - \alpha } \right) - \cos \left( {13\pi + \alpha } \right)\).
Bài 3 trang 19 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tính các giá trị lượng giác của góc α, nếu:
Bài 4 trang 19 SGK Toán 11 tập 1 - Chân trời ság tạo
Biểu diễn các giá trị lượng giác sau qua giá trị lượng giác của góc có số đo từ 0 đến (frac{pi }{4}) hoặc từ 0 đến (45^circ ) và tính
Bài 5 trang 19 SGK Toán 11 tập 1 - Chân trời ság tạo
Chứng minh các đẳng thức lượng giác sau: a) ({sin ^4}alpha - {cos ^4}alpha
Bài 6 trang 19 SGK Toán 11 tập 1 - Chân trời ság tạo
Rút gọn các biểu thức sau: a) (frac{1}{{tan alpha + 1}} + frac{1}{{cot alpha + 1}})
Bài 7 trang 20 SGK Toán 11 tập 1 - Chân trời ság tạo
Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được (3frac{1}{{10}}) vòng là bao nhiêu, biết thanh độ dài OM là 15cm? Kết quả làm trong đến hàng phần mười.
Bài 8 trang 20 SGK Toán 11 tập 1 - Chân trời sáng tạo
Khi xe đạp di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58cm? Giả sử độ dày của lốp xe không đáng kể. Kết quả làm trong đến hàng phần mười.
Giải câu hỏi mở đầu trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo
Hình bên biểu diễn xích đu IA có độ dài 2 m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi là li độ của A và \(\left( {IO,IA} \right) = \alpha \) được gọi là li độ góc của A. Làm cách nào để tính li độ dựa vào li độ góc?
Lý thuyết Giá trị lượng giác của một góc lượng giác - SGK Toán 11 Chân trời sáng tạo
1. Giá trị lượng giác của góc lượng giác