Giải bài tập 5 trang 58 SGK Toán 12 tập 1 - Chân trời sáng tạo

Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5, giao điểm hai đường chéo AC và BD trùng với gốc O. Các vectơ (overrightarrow {OB} ,overrightarrow {OC} ,overrightarrow {OS} )¬ lần lượt cùng hướng với (overrightarrow i ), (overrightarrow j ), (overrightarrow k ) và OA = OS = 4 (Hình 15). Tìm toạ độ các vectơ (overrightarrow {AB} ,overrightarrow {AC} ,overrightarrow {AS} ) và (overrightarrow {AM} )¬ ¬với M là trung điểm của cạnh SC.

Tổng hợp đề thi giữa kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

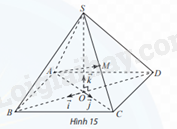
Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5, giao điểm hai đường chéo AC và BD trùng với gốc O. Các vectơ \(\overrightarrow {OB} ,\overrightarrow {OC} ,\overrightarrow {OS} \) lần lượt cùng hướng với \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) và OA = OS = 4 (Hình 15). Tìm toạ độ các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AS} \) và \(\overrightarrow {AM} \) với M là trung điểm của cạnh SC.

Phương pháp giải - Xem chi tiết

Quan sát hình vẽ. Tìm tọa độ các điểm A, B, C, S và M rồi tính tọa độ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AS} \) và \(\overrightarrow {AM} \).

Lời giải chi tiết

Xét tam giác OAB vuông tại O: \(OB = \sqrt {A{B^2} - O{A^2}} = \sqrt {{5^2} - {4^2}} = 3\)

Ta có: \(\overrightarrow {OA} = - 4\overrightarrow j = > A(0; - 4;0)\)

\(\overrightarrow {OB} = 3\overrightarrow i = > B(3;0;0)\)

=> \(\overrightarrow {AB} = 3\overrightarrow i - 4\overrightarrow j = (3; - 4;0)\)

\(\overrightarrow {OC} = 4\overrightarrow j = > C(0;4;0)\) => \(\overrightarrow {AC} = 8\overrightarrow j = (0;8;0)\)

\(\overrightarrow {OS} = 4\overrightarrow k = > S(0;0;4)\) => \(\overrightarrow {AS} = 4\overrightarrow j + 4\overrightarrow k = (0;4;4)\)

\(\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OS} + \overrightarrow {OC} ) = \frac{1}{2}(4\overrightarrow k + 4\overrightarrow j ) = 2\overrightarrow j + 2\overrightarrow k = > \overrightarrow {OM} = (0;2;2) \Rightarrow M(0;2;2)\)

=> \(\overrightarrow {AM} = 6\overrightarrow j + 2\overrightarrow k = (0;6;2)\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo
Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ Oxyz như Hình 16 với độ dài đơn vị trên các trục toạ độ bằng 1 m. Tìm toạ độ của vectơ \(\overrightarrow {AB} \)
Giải bài tập 7 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo
Ở một sân bay, ví trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình 17. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, \((\overrightarrow i ;\overrightarrow {OH} ) = 64^\circ \), \((\overrightarrow {OH} ;\overrightarrow {OM} ) = 48^\circ \). Tìm toạ độ của điểm M.
Giải bài tập 4 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA bằng 1 (Hình 14). Thiết lập hệ toạ độ như hình vẽ, hãy vẽ các vectơ đơn vị trên các trục Ox, Oy, Oz và tìm toạ độ các điểm A, B, C, S.
Giải bài tập 3 trang 56 SGK Toán 12 tập 1 - Chân trời sáng tạo
Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13). a) Xác định một hệ toạ độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục toạ độ. b) Tìm toạ độ các điểm A, B, C, S.
Giải bài tập 2 trang 56 SGK Toán 12 tập 1 - Chân trời sáng tạo
Trong không gian Oxyz, biết: a) (overrightarrow a = ( - 2;5; - 7)), (overrightarrow b = (4;0;1)). Tính (overrightarrow a ), (overrightarrow b ), theo các vectơ (overrightarrow i ), (overrightarrow j ), (overrightarrow k ) b) A(7; –2; 1), B(0; 5; 0). Tính (overrightarrow {OA} ), (overrightarrow {OB} ) theo các vectơ (overrightarrow i ), (overrightarrow j ), (overrightarrow k )
Giải bài tập 1 trang 56 SGK Toán 12 tập 1 - Chân trời sáng tạo
Trong không gian Oxyz, biết: a) (overrightarrow a = 5overrightarrow i + 7overrightarrow j - 3overrightarrow k ), (overrightarrow b = 2overrightarrow i + 4overrightarrow k ). Tìm toạ độ các vectơ (overrightarrow a ), (overrightarrow b ) b) (overrightarrow {OM} = 4overrightarrow i - overrightarrow j + 3overrightarrow k ), (overrightarrow {ON} = 8overrightarrow i - 5overrightarrow j ). Tìm toạ độ các điểm M, N.
Giải mục 2 trang 53,54,55 SGK Toán 12 tập 1 - Chân trời sáng tạo
Toạ độ của điểm và vectơ
Giải mục 1 trang 52,53 SGK Toán 12 tập 1 - Chân trời sáng tạo
Hệ toạ độ trong không gian
Lý thuyết Tọa độ của vecto trong không gian Toán 12 Chân trời sáng tạo
Bài 2. Tọa độ của vecto trong không gian 1. Hệ trục tọa độ trong không gian