 Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
 Bài 2. Tiếp tuyến của đường tròn - Toán 9 Chân trời sán..
Bài 2. Tiếp tuyến của đường tròn - Toán 9 Chân trời sán..
Giải bài tập 4 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
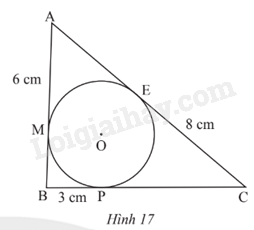
Cho tam giác ABC có đương tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm; BP = 3 cm; CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
Đề bài
Cho tam giác ABC có đương tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm; BP = 3 cm; CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Dựa vào tính chất hai tiếp tuyến cắt nhau để chứng minh BM = BP, AM = AE, CE = CP.
- Tính chu vi tam giác bằng AB + AC + BC.
Lời giải chi tiết
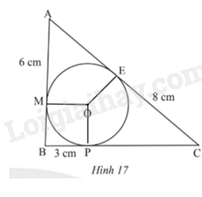
Ta có MB và BP là hai tiếp tuyến tại M và P của đường tròn (O) và cắt nhau tại B.
Do đó: BM = BP = 3cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có AM và AE là hai tiếp tuyến tại M và E của đường tròn (O) và cắt nhau tại A.
Do đó: AM = AE = 6cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có CE và CP là hai tiếp tuyến tại E và P của đường tròn (O) và cắt nhau tại C.
Do đó: CE = CP = 8cm (Tính chất hai tiếp tuyến cắt nhau).
Suy ra chu vi tam giác ABC là:
AB + AC + BC = (AM + MB) + (AE + EC) + (BP + PC)
= (6 + 3) + (6 + 8) + (3 + 8) = 34 cm.
- Giải bài tập 5 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 6 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 7 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 8 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 3 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay












Danh sách bình luận