Giải bài tập 3 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo

Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ. a) Tính số đo mỗi cung b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng (frac{{AB}}{2}). Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ. a) Tính số đo mỗi cung b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng (frac{{AB}}{2}).

Đề bài

Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.

a) Tính số đo mỗi cung

b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng \(\frac{{AB}}{2}\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Đọc dữ kiện đề bài để vẽ hình.

- Gọi \(\overset\frown{AnB}\) là cung nhỏ và \(\overset\frown{AmB}\) là cung lớn rồi lập biểu thức theo đề bài để tính.

- Chứng minh H là trung điểm AB.

Lời giải chi tiết

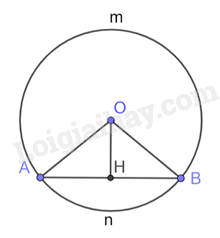
a) Gọi \(\overset\frown{AnB}\) là cung nhỏ và \(\overset\frown{AmB}\) là cung lớn có sđ\(\overset\frown{AmB}\) = 3sđ\(\overset\frown{AnB}\) (gt)

Mà sđ\(\overset\frown{AmB}\) + sđ\(\overset\frown{AnB}\) = 360^o

Do đó 4sđ\(\overset\frown{AnB}\) = 360^o

sđ\(\overset\frown{AnB}\) = 360^o: 4 = 90^o

Vậy sđ\(\overset\frown{AmB}\) = 3sđ\(\overset\frown{AnB}\) = 3. 90^o = 270^o .

b) Ta có \(\widehat {AOB}\)= sđ\(\overset\frown{AnB}\) (góc ở tâm chắn cung AB)

suy ra \(\widehat {AOB}\)= 90^o suy ra tam giác AOB vuông tại O.

Mà AO = OB = R nên tam giác AOB vuông cân tại O.

Khi đó OH là đường cao đồng thời là đường trung tuyến.

Tam giác AOB vuông tại O có OH là đường trung tuyến ứng với cạnh huyền nên OH = \(\frac{{AB}}{2}\).

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Giải bài tập 4 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo
Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu vào những thời điểm sau? a) 2 giờ b) 8 giờ c) 21 giờ
Giải bài tập 5 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hai đường tròn đồng tâm (O; R) và (O; (frac{{Rsqrt 3 }}{2})). Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB.
Giải bài tập 6 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo
Xác định số đo các cung (oversetfrown{AB};oversetfrown{BC};oversetfrown{CA}) trong mỗi hình vẽ sau:
Giải bài tập 7 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng (widehat {MSD} = 2widehat {MBA}).
Giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung (oversetfrown{BD};oversetfrown{BE};oversetfrown{EC}).
Giải bài tập 1 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.
Giải mục 3 trang 93, 94, 95 SGK Toán 9 tập 1 - Chân trời sáng tạo
Quan sát Hình 13. Hãy cho biết trong các góc (widehat {APB};widehat {AOB};widehat {AMB};widehat {AQB}), góc nào có đỉnh nằm trên đường tròn (O).
Giải mục 2 trang 91, 92, 93 SGK Toán 9 tập 1 - Chân trời sáng tạo
Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.
Giải mục 1 trang 90, 91 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của (widehat {AOB})
Lý thuyết Góc ở tâm, góc nội tiếp Toán 9 Chân trời sáng tạo
1. Góc ở tâm Định nghĩa Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.