Giải bài tập 23 trang 30 SGK Toán 12 tập 2 - Chân trời sáng tạo

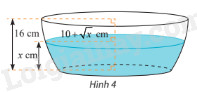
Nếu cắt chậu nước có hình dạng như hình dưới đây bằng mặt phẳng song song và cách mặt đáy (x) (cm) (left( {0 le x le 16} right)) thì mặt cắt là hình tròn có bán kính (left( {10 + sqrt x } right)) (cm). Tính dung tích của chậu.

Đề bài

Nếu cắt chậu nước có hình dạng như hình 4 bằng mặt phẳng song song và cách mặt đáy \(x\) (cm) \(\left( {0 \le x \le 16} \right)\) thì mặt cắt là hình tròn có bán kính \(\left( {10 + \sqrt x } \right)\) (cm). Tính dung tích của chậu.

Phương pháp giải - Xem chi tiết

Chọn trục \(Ox\) sao cho \(O\) trùng với tâm của đáy, chiều dương của trục là chiều hướng lên trên.

Khi cắt chậu nước bằng mặt phẳng song song với đáy và cách mặt đáy \(x\), thì mặt phẳng đó cắt trục \(Ox\) tại điểm có hoành độ \(x\). Diện tích mặt cắt là \(S\left( x \right)\).

Suy ra dung tích của chậu là \(V = \int\limits_0^{16} {S\left( x \right)dx} \).

Lời giải chi tiết

Chọn trục \(Ox\) sao cho \(O\) trùng với tâm của đáy, chiều dương của trục là chiều hướng lên trên.

Khi cắt chậu nước bằng mặt phẳng song song với đáy và cách mặt đáy \(x\), thì mặt phẳng đó cắt trục \(Ox\) tại điểm có hoành độ \(x\). Mặt cắt là hình tròn có bán kính \(\left( {10 + \sqrt x } \right)\) (cm)

Như vậy, diện tích mặt cắt là \(S\left( x \right) = \pi {\left( {10 + \sqrt x } \right)^2} = \pi \left( {x + 100 + 20\sqrt x } \right)\).

Suy ra dung tích của chậu là

\(V = \int\limits_0^{16} {S\left( x \right)dx} = \int\limits_0^{16} {\pi \left( {x + 100 + 20\sqrt x } \right)dx} = \pi \left. {\left( {\frac{{{x^2}}}{2} + 100x + 20.\frac{2}{3}\sqrt {{x^3}} } \right)} \right|_0^{16} = \frac{{7744}}{3}\pi \) (\({\rm{c}}{{\rm{m}}^3}\)).