Giải Bài 3 trang 58 sách bài tập toán 7 - Chân trời sáng tạo

Cho tam giác ABC có góc A bằng \({120^o}\). Các đường trung trực của AB và Ac lần lượt cắt Bc tại M và N. Tính số đo góc MAN.

Đề bài

Cho tam giác ABC có góc A bằng \({120^o}\). Các đường trung trực của AB và Ac lần lượt cắt Bc tại M và N. Tính số đo góc MAN.

Phương pháp giải - Xem chi tiết

Sử dụng tính chất của tam giác cân

Lời giải chi tiết

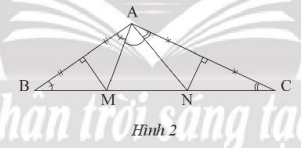
Ta có MA = MB suy ra tam giác MAB cân tại M suy ra \(\widehat {MAB} = \widehat {MBA} = \widehat B\)

Tương tự, ta có tam giác NAC cân tại N suy ra \(\widehat {NAC} = \widehat {NCA} = \widehat C\)

Ta có: \(\widehat {MAN} = \widehat {BAC} - \left( {\widehat {MAB} + \widehat {NAC}} \right) = {120^o} - \left( {\widehat B + \widehat C} \right) = {120^o} - {60^o} = {60^o}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải Bài 4 trang 58 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có góc A là góc từ. Các đường trung trực của AB và Ac cắt nhau tại O và lần lượt cắt BC tại E và F. Hãy chứng minh
Giải Bài 5 trang 58 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có đường trung trực cạnh AC đi qua đỉnh B, chứng minh tam giác ABC là tam giác cân
Giải Bài 2 trang 57 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác đều ABC và điểm G như trong hình 8. Hãy chứng minh GA = GB = GC.
Giải Bài 1 trang 57 sách bài tập toán 7 - Chân trời sáng tạo
Điểm O trong hình 7 có phải là giao điểm của ba đường trung trực của tam giác ABC hay không? Hãy giải thích.