Giải bài 19 trang 76 sách bài tập toán 11 - Cánh diều

Quan sát đồ thị hàm số ở hình dưới đây và cho biết các giới hạn sau

Đề bài

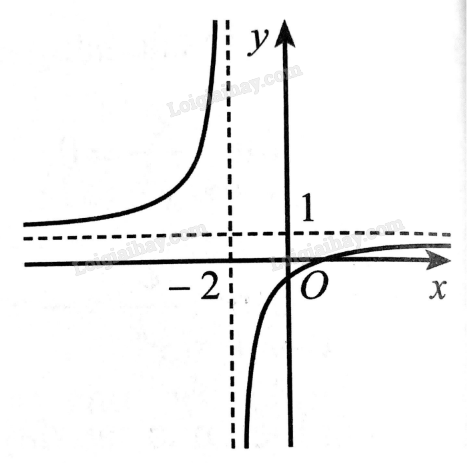
Quan sát đồ thị hàm số ở hình dưới đây và cho biết các giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right)\).

Phương pháp giải - Xem chi tiết

Từ đồ thị, để tìm\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\), ta cần xác định khi \(x\) dần tới dương vô cực thì \(f\left( x \right)\) dần tới đâu. Tương tự với \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right)\).

Lời giải chi tiết

Từ đồ thị, ta nhận thấy rằng:

+ Khi \(x\) dần tới dương vô cực thì \(f\left( x \right)\) dần tới 1. Như vậy \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\).

+ Khi \(x\) dần tới âm vô cực thì \(f\left( x \right)\) dần tới 1. Như vậy \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 1\).

+ Khi \(x\) dần tới \( - 2\) về bên phải thì \(f\left( x \right)\) dần tới âm vô cực. Như vậy \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = - \infty \).

+ Khi \(x\) dần tới \( - 2\) về bên trái thì \(f\left( x \right)\) dần tới dương vô cực. Như vậy \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right) = + \infty \).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 20 trang 76 sách bài tập toán 11 - Cánh diều
Tính các giới hạn sau:
Giải bài 21 trang 76 sách bài tập toán 11 - Cánh diều
Tính các giới hạn sau:
Giải bài 22 trang 76 sách bài tập toán 11 - Cánh diều
Cho \(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - 4}}{{x - 1}} = 2\). Tính
Giải bài 23 trang 76 sách bài tập toán 11 - Cánh diều
Cho hàm số \(f\left( x \right)\) thoả mãn \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2022\).
Giải bài 24 trang 76 sách bài tập toán 11 - Cánh diều
Cho số thực \(a\) và hàm số \(f\left( x \right)\) thoả mãn \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = - \infty \).
Giải bài 25 trang 76 sách bài tập toán 11 - Cánh diều
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên biến đổi theo một hàm số thời gian (tính theo ngày)
Giải bài 18 trang 75 sách bài tập toán 11 - Cánh diều
Cho \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = 4\), chứng minh rằng:
Giải bài 17 trang 75 sách bài tập toán 11 - Cánh diều
Sử dụng định nghĩa, chứng minh rằng:
Giải bài 16 trang 75 sách bài tập toán 11 - Cánh diều
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Phát biểu nào sau đây là đúng?
Giải bài 15 trang 75 sách bài tập toán 11 - Cánh diều
Phát biểu nào sau đây là đúng?
Giải bài 14 trang 75 sách bài tập toán 11 - Cánh diều
Với \(c\), \(k\) là các hằng số và \(k\) nguyên dương thì
Giải bài 13 trang 74 sách bài tập toán 11 - Cánh diều
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {{x_0},b} \right)\). Phát biểu nào sau đây là đúng?
Giải bài 12 trang 74 sách bài tập toán 11 - Cánh diều
Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\) \(\left( {L,M \in \mathbb{R}} \right)\).