Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo

Bài tập cuối chuyên đề 1 Chuyên đề học tập Toán 11 Chân..

Giải bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Cho tam giác ABC có góc B, góc C đều là góc nhọn.

Đã có lời giải SGK Toán lớp 12 - Chân trời sáng tạo (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Cho tam giác ABC có góc B, góc C đều là góc nhọn. Nêu cách vẽ hình chữ nhật DEFG có đỉnh D, đỉnh E thuộc cạnh BC, đỉnh F, đỉnh G thuộc cạnh AC, AB và có EF = 2DE.

Phương pháp giải - Xem chi tiết

Dựa vào phép vị tự để làm: Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.

Lời giải chi tiết

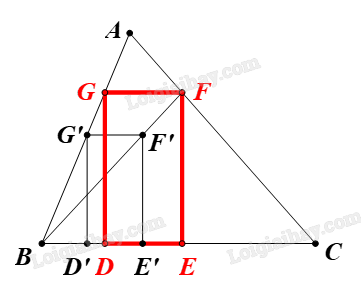
⦁ Phân tích:

Lấy điểm G’ bất kì trên AB.

Dựng hình chữ nhật D’E’F’G’ có \(\;E'F'{\rm{ }} = {\rm{ }}2D'E'\) và hai đỉnh D’, E’ thuộc BC.

Đường thẳng BF’ cắt AC tại F.

Do D’E’F’G’ là hình chữ nhật nên \(G'D'{\rm{ }} \bot {\rm{ }}D'E'\) hay \(G'D'{\rm{ }} \bot {\rm{ }}BC.\)

Mà GD ⊥ BC (do DEFG là hình chữ nhật).

Nên G’D’ // GD.

Chứng minh tương tự, ta được E’F’ // EF.

Vì D’E’F’G’ là hình chữ nhật nên G’F’ // D’E’ hay G’F’ // BC.

Mà GF // BC (do DEFG là hình chữ nhật).

Suy ra GF // G’F’.

Áp dụng định lí Thales, ta được \(\frac{{BG}}{{BG'}} = \frac{{BF}}{{BF'}}\)

Suy ra \(BF' = \frac{{BG'}}{{BG}}.BF\)

Mà \(\overrightarrow {BF'} ,\overrightarrow {BF} \) cùng hướng.

Do đó \(\overrightarrow {BF'} = \frac{{BG'}}{{BG}}.\overrightarrow {BF} \)

Vì vậy \({\rm{F'}} = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( F \right)\,\,(1)\)

Chứng minh tương tự, ta được \(D' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( D \right)\) và \(E' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( E \right)\,\,(2)\)

Lại có \(G' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( G \right)\,\,(3)\)

Từ (1), (2), (3), ta thu được \({V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\) biến hình chữ nhật D’E’F’G’ thành hình chữ nhật DEFG. Từ đó, ta suy ra cách dựng hình chữ nhật DEFG.

⦁ Cách dựng:

Lấy điểm G’ tùy ý trên AB.

Dựng hình chữ nhật D’E’F’G’ có E’F’ = 2D’E’, hai đỉnh D’, E’ nằm trên BC.

Đường thẳng BF’ cắt AC tại F.

Đường thẳng qua F song song với BC cắt AB tại G.

Gọi D, E lần lượt là hình chiếu của G, F lên BC.

Vậy ta đã dựng xong hình chữ nhật DEFG.

Bình luận

Chia sẻ

Bình chọn:

4 trên 4 phiếu

Giải bài 17 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Thấu kính hội tụ có thể cho ảnh thật hoặc ảnh ảo A’B’ của vật AB. Tìm phép vị tự biến AB thành A’B’ trong Hình 3 và Hình 4.
Giải bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Gọi O được gọi là tâm đối xứng quay bậc (n{rm{ }}(n in mathbb{N}*)) của hình ℋ nếu sau khi thực hiện phép quay ({Q_{left( {O,frac{{360^circ }}{n}} right)}})
Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tìm phép biến hình f biến hình (A) thành hình (B).
Giải bài 14 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho (Mleft( {3;{rm{ }}2} right),{rm{ }}Nleft( {2;{rm{ }}0} right).)
Giải bài 13 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d:{rm{ }}x{rm{ }} + {rm{ }}6y{rm{ }}-{rm{ }}5{rm{ }} = {rm{ }}0.)
Giải bài 12 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho đường thẳng \(d:{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0,\;\) đường tròn \(\left( C \right):{\rm{ }}{x^2}\; + {\rm{ }}{y^2}\;-{\rm{ }}4x{\rm{ }} + {\rm{ }}8y{\rm{ }}-{\rm{ }}5{\rm{ }} = {\rm{ }}0.\)
Giải bài 11 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho điểm A chạy trên nửa đường tròn đường kính BC cố định.
Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho đường tròn (O; R) và điểm I cố định khác O. Vẽ điểm M tùy ý trên (O). Tia phân giác của góc MOI cắt IM tại N. Điểm N di động trên đường nào khi M di động trên (O)?
Giải bài 9 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho tam giác ABC. Vẽ về phía ngoài của tam giác các hình vuông ABEF, ACMN. Chứng minh BN bằng và vuông góc với FC.
Giải bài 8 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho điểm M(–2; 4). Phép vị tự tâm O tỉ số \(k = -2\) biến điểm M thành điểm nào trong các điểm sau?
Giải bài 7 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O với góc quay \(\alpha \), \(0{\rm{ }} < {\rm{ }}\alpha {\rm{ }} \le {\rm{ }}2\pi ,\)biến tam giác trên thành chính nó?
Giải bài 6 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O với góc quay 45°?
Giải bài 5 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?
Giải bài 4 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x = 2.
Giải bài 3 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình ℋ. Hỏi ℋ có mấy trục đối xứng?
Giải bài 2 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Oy, điểm A(3; 5) biến thành điểm nào trong các điểm sau?
Giải bài 1 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 5). Phép tịnh tiến theo vectơ \(\vec v = \left( {1;2} \right)\) biến điểm M thành điểm có tọa độ là

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.