 Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
 Bài 5. Phép quay Chuyên đề học tập Toán 11 Chân trời sá..
Bài 5. Phép quay Chuyên đề học tập Toán 11 Chân trời sá..
Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
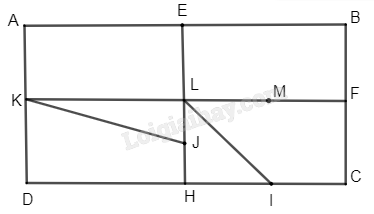
Cho hình chữ nhật ABCD. Gọi E, F, H, K, L, I, J lần lượt là trung điểm của AB, BC, CD, DA, KF, HC, HL. Chứng minh hình thang AEJK và hình thang FLIC bằng nhau.
Đề bài
Cho hình chữ nhật ABCD. Gọi E, F, H, K, L, I, J lần lượt là trung điểm của AB, BC, CD, DA, KF, HC, HL. Chứng minh hình thang AEJK và hình thang FLIC bằng nhau.
Lời giải chi tiết
Gọi M là trung điểm của LF.
Ta thấy phép đối xứng qua EH biến hình thang AEJK thành hình thang BEMF; phép tịnh tiến theo vectơ \(\overrightarrow {BF} \) biến hình thang BEMF thành hình thang FLIC.
Như vậy, phép dời hình có được bằng cách thực hiện liên tiếp phép biến hình trên sẽ biến hình thang AEJK thành hình thang FLIC.
Do đó hai hình thang AEJK và FLIC bằng nhau.
- Giải bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 5 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 2 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo












Danh sách bình luận