Đề thi giữa kì 2 Toán 8 - Đề số 4 - Chân trời sáng tạo
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Khoa học tự nhiên
Câu 1: (150984) Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng
Đề bài
Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}\). Quãng đường mà vật đó chuyển động được sau 3 giây là :
-
A.
20m.
-
B.
45m.
-
C.
50m.
-
D.
60.
-
A.
y = - 2 x .
-
B.
y = - 0,5x.
-
C.
y = \(\frac{1}{2}\)x .
-
D.
y = 2 x.
Xác định đường thẳng \(y = ax + b;(a \ne 0)\) có hệ số góc bằng 2 và đi qua điểm A (2;1)
-
A.
\(y = - 2x + 3\).
-
B.
\(y = 2x - 3\).
-
C.
\(y = - 2x - 3\).
-
D.
\(y = 2x + 5\).
“Trên mặt phẳng, ta vẽ hai trục số Ox, Oy …… với nhau và ……. tại gốc tọa độ O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy”. Các từ lần lượt cần điền đó là :
-
A.
song song; vuông góc .
-
B.
vuông góc; trùng nhau.
-
C.
vuông góc; cắt nhau.
-
D.
trùng; cắt nhau.
Trong các hàm số sau hàm số có hệ số góc dương là:
-
A.
\(y = 1 - x\).
-
B.
\(y = \frac{2}{3} - 2x\).
-
C.
\(y = 2x + 1\).
-
D.
\(y = 6 - 2\left( {x + 1} \right)\).
Nếu \(P\left( {1; - 2} \right)\) thuộc đường thẳng \(x - y = m\) thì m bằng:
-
A.
\(m = - 1\).
-
B.
\(m = 1\).
-
C.
\(m = 3\).
-
D.
\(m = - 3\).
Cho tam giác ABC có AB = 9cm; \(D \in AB\) sao cho AD = 6cm. Kẻ DE // BC (\(E \in AC\)); EF // CD (\(F \in AB\)). Tính độ dài AF.
-
A.
6cm.
-
B.
5cm.
-
C.
4cm.
-
D.
7cm.
Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó, tứ giác MNED là hình gì?
-
A.
Hình chữ nhật.
-
B.
Hình bình hành.
-
C.
Hình thang cân.
-
D.
Hình thang vuông.
Cho tam giác ABC, AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} =?\)
-
A.
\(\frac{{BD}}{{CD}} = 1\).
-
B.
\(\frac{{BD}}{{CD}} = \frac{1}{3}\).
-
C.
\(\frac{{BD}}{{CD}} = \frac{1}{4}\).
-
D.
\(\frac{{BD}}{{CD}} = \frac{1}{2}\).
-
A.
8.
-
B.
10.
-
C.
12.
-
D.
14.
Để đo chiều cao AC của một cột cờ (như hình vẽ), người ta cắm một cái cọc ED có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại B, biết khoảng cách BE là 1,5m và khoảng cách AB là 9m.
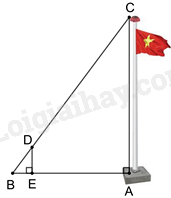
Khi đó chiều cao AC của cột cờ là:
-
A.
12m.
-
B.
6,75m.
-
C.
3m.
-
D.
4m.
Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Gọi P, Q lần lượt là trung điểm của AB, AC. Khi đó độ dài PQ là:
-
A.
2,5cm.
-
B.
10cm.
-
C.
1,5cm.
-
D.
2cm.
Lời giải và đáp án
Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}\). Quãng đường mà vật đó chuyển động được sau 3 giây là :
-
A.
20m.
-
B.
45m.
-
C.
50m.
-
D.
60.
Đáp án : B
Thay x = 3 vào hàm số.
Với x = 3 thì \(y = {5.3^2} = 45\)(m).
Vậy quãng đường mà vật đó chuyển động được sau 3 giây là 45m.
-
A.
y = - 2 x .
-
B.
y = - 0,5x.
-
C.
y = \(\frac{1}{2}\)x .
-
D.
y = 2 x.
Đáp án : B
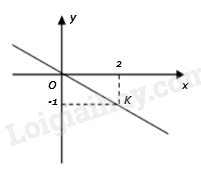
Quan sát đồ thị để xác định điểm O; K.
Ta có tọa độ điểm O là O(0; 0); tọa độ điểm K là K(2; -1).
Gọi hàm số cần tìm là \(y = ax + b\left( {a \ne 0} \right)\).
Vì đồ thị của hàm số đi qua điểm O(0; 0) và điểm K nên ta có:
\(0 = a.0 + b\)\( \Leftrightarrow \)\(b = 0 \Rightarrow y = ax\)
\( - 1 = a.2\)\( \Leftrightarrow \)\(a = \frac{{ - 1}}{2}\)\( \Rightarrow y = - \frac{1}{2}x = y = - 0,5x\).
* Học sinh cũng có thể thay tọa độ điểm O và K vào các hàm số trong đáp án để tìm hàm số.
Xác định đường thẳng \(y = ax + b;(a \ne 0)\) có hệ số góc bằng 2 và đi qua điểm A (2;1)
-
A.
\(y = - 2x + 3\).
-
B.
\(y = 2x - 3\).
-
C.
\(y = - 2x - 3\).
-
D.
\(y = 2x + 5\).
Đáp án : B
Dựa vào kiến thức về hệ số góc và hàm số bậc nhất để xác định.
Vì đường thẳng có hệ số góc bằng 2 nên a = 2 => y = 2x + b.
Vì đường thẳng đi qua điểm A(2; 1) nên 1 = 2.2 + b hay b = -3 => y = 2x - 3.
“Trên mặt phẳng, ta vẽ hai trục số Ox, Oy …… với nhau và ……. tại gốc tọa độ O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy”. Các từ lần lượt cần điền đó là :
-
A.
song song; vuông góc .
-
B.
vuông góc; trùng nhau.
-
C.
vuông góc; cắt nhau.
-
D.
trùng; cắt nhau.
Đáp án : C
Dựa vào kiến thức về mặt phẳng tọa độ.
“Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc tọa độ O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy”
Trong các hàm số sau hàm số có hệ số góc dương là:
-
A.
\(y = 1 - x\).
-
B.
\(y = \frac{2}{3} - 2x\).
-
C.
\(y = 2x + 1\).
-
D.
\(y = 6 - 2\left( {x + 1} \right)\).
Đáp án : C
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\) với a là hệ số.
Hàm số có hệ số góc dương thì a > 0.
Hàm số \(y = 1 - x\) có hệ số góc âm ( a = -1 < 0)
Hàm số \(y = \frac{2}{3} - 2x\) có hệ số góc âm (a = -2 < 0)
Hàm số \(y = 2x + 1\) có hệ số góc dương (a = 2 > 0)
Hàm số \(y = 6 - 2\left( {x + 1} \right) = 6 - 2x - 2 = - 2x + 4\) có hệ số góc âm (a = -2 < 0)
Nếu \(P\left( {1; - 2} \right)\) thuộc đường thẳng \(x - y = m\) thì m bằng:
-
A.
\(m = - 1\).
-
B.
\(m = 1\).
-
C.
\(m = 3\).
-
D.
\(m = - 3\).
Đáp án : C
Thay tọa độ điểm P vào đường thẳng để tìm m.
Vì \(P\left( {1; - 2} \right)\) thuộc đường thẳng \(x - y = m\) nên ta có:
\(1 - \left( { - 2} \right) = m \Rightarrow m = 3\).
Cho tam giác ABC có AB = 9cm; \(D \in AB\) sao cho AD = 6cm. Kẻ DE // BC (\(E \in AC\)); EF // CD (\(F \in AB\)). Tính độ dài AF.
-
A.
6cm.
-
B.
5cm.
-
C.
4cm.
-
D.
7cm.
Đáp án : C
Sử dụng định lí Thales để chứng minh.
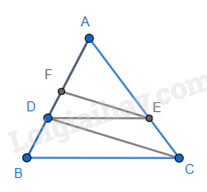
Ta có: DE // BC nên \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{6}{9} = \frac{2}{3}\) (định lí Thales)
EF // CD nên \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}} = \frac{2}{3}\) (định lí Thales)
\( \Rightarrow AF = \frac{2}{3}AD = \frac{2}{3}.6 = 4(cm)\).
Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó, tứ giác MNED là hình gì?
-
A.
Hình chữ nhật.
-
B.
Hình bình hành.
-
C.
Hình thang cân.
-
D.
Hình thang vuông.
Đáp án : B
Sử dụng tính chất đường trung bình.
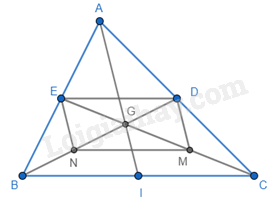
Ta có BD và CE là đường trung tuyến của tam giác ABC nên D là trung điểm của AC; E là trung điểm của AB, khi đó DE là đường trung bình của tam giác ABC nên DE // BC và DE = \(\frac{1}{2}\)BC. (1)
M và N lần lượt là trung điểm của GC và GB nên MN là đường trung bình của tam giác GBC nên MN // BC và MN = \(\frac{1}{2}\)BC. (2)
Từ (1) và (2) suy ra DE // MN và DE = MN => MNED là hình bình hành (hai cạnh đối song song và bằng nhau).
Cho tam giác ABC, AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} =?\)
-
A.
\(\frac{{BD}}{{CD}} = 1\).
-
B.
\(\frac{{BD}}{{CD}} = \frac{1}{3}\).
-
C.
\(\frac{{BD}}{{CD}} = \frac{1}{4}\).
-
D.
\(\frac{{BD}}{{CD}} = \frac{1}{2}\).
Đáp án : D
Sử dụng tính chất của đường phân giác trong tam giác.
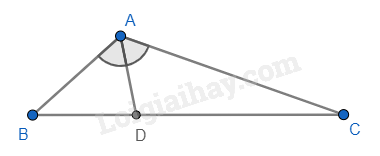
Ta có AD là tia phân giác của tam giác ABC nên \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = \frac{{AB}}{{2AB}} = \frac{1}{2}\) (tính chất của tia phân giác trong tam giác).
-
A.
8.
-
B.
10.
-
C.
12.
-
D.
14.
Đáp án : D
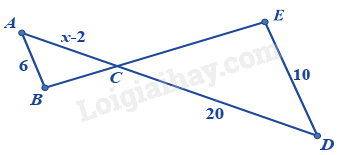
Áp dụng hệ quả của định lí Thales để tính độ dài đoạn thẳng AC. Từ đó tính được x.
Xét tam giác CDE có AB // DE nên ta có:
\(\begin{array}{l}\frac{{AC}}{{AB}} = \frac{{CD}}{{DE}}\\\frac{{x - 2}}{6} = \frac{{20}}{{10}} = 2\\ \Rightarrow x - 2 = 2.6 = 12\\ \Rightarrow x = 14\end{array}\)
Để đo chiều cao AC của một cột cờ (như hình vẽ), người ta cắm một cái cọc ED có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại B, biết khoảng cách BE là 1,5m và khoảng cách AB là 9m.
Khi đó chiều cao AC của cột cờ là:
-
A.
12m.
-
B.
6,75m.
-
C.
3m.
-
D.
4m.
Đáp án : A
Sử dụng hệ quả của định lí Thales.
Vì cột cờ AC và cọc DE cùng vuông góc với mặt đất nên AC // DE.
Xét tam giác ABC có AC // DE nên ta có:
\(\begin{array}{l}\frac{{AC}}{{DE}} = \frac{{AB}}{{BE}}\\\frac{{AC}}{2} = \frac{9}{{1,5}}\\ \Rightarrow AC = \frac{{9.2}}{{1,5}} = 12\left( m \right)\end{array}\)
Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Gọi P, Q lần lượt là trung điểm của AB, AC. Khi đó độ dài PQ là:
-
A.
2,5cm.
-
B.
10cm.
-
C.
1,5cm.
-
D.
2cm.
Đáp án : A
Sử dụng định lí Pythagore để tính BC. Dựa vào tính chất đường trung bình để tính PQ.
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25\\ \Rightarrow BC = \sqrt {25} = 5\left( {cm} \right)\end{array}\)
Vì P, Q lần lượt là trung điểm của AB và AC nên PQ là đường trung bình của tam giác ABC.
\( \Rightarrow PQ = \frac{1}{2}BC = \frac{1}{2}.5 = 2,5\left( {cm} \right)\)
a) Lấy hai điểm thuộc hàm số để vẽ đồ thị hàm số.
b) Giải phương trình hoành độ giao điểm của hai đường thẳng để tìm tọa độ giao điểm.
c) Thay tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) vào \(\left( {{d_3}} \right)\) để tìm m.
a) Vẽ \(\left( {{d_1}} \right):y = x - 4\)
+ Cho x = 0 thì y = 0 – 4 = -4. Ta được điểm A(0; -4).
+ Cho y = 0 thì 0 = x – 4 => x = 4. Ta được điểm B(4; 0).
Đường thẳng AB chính là đường thẳng \(\left( {{d_1}} \right)\).
Vẽ \(\left( {{d_2}} \right):y = - 3x + 2\)
+ Cho \(x = 0\) thì \(y = - 3.0 + 2 = 2\). Ta được điểm \(C\left( {0;2} \right)\).
+ Cho \(y = 0\) thì \(0 = - 3x + 2 \Rightarrow x = \frac{2}{3}\). Ta được điểm \(D\left( {\frac{2}{3};0} \right)\).
Đường thẳng CD chính là đường thẳng \(\left( {{d_1}} \right)\).
Ta có đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\):
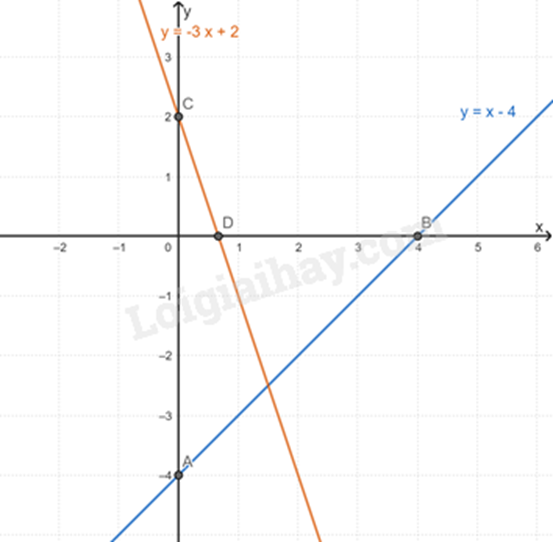
b) Phương trình hoành độ giao điểm của hai đường thẳng là:
\(\begin{array}{l}x - 4 = - 3x + 2\\x + 3x = 2 + 4\\4x = 6\\x = \frac{3}{2}\end{array}\)
\( \Rightarrow y = \frac{3}{2} - 4 = - \frac{5}{2}\).
Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(E\left( {\frac{3}{2};\frac{{ - 5}}{2}} \right)\).
c) Vì \(\left( {{d_3}} \right)\) đi qua tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) nên \(E\left( {\frac{3}{2};\frac{{ - 5}}{2}} \right) \in \left( {{d_3}} \right)\).
Thay tọa độ điểm E vào hàm số \(y = \left( {m - 2} \right)x + 3m + 12\), ta được:
\(\begin{array}{l}\frac{{ - 5}}{2} = \left( {m - 2} \right).\frac{3}{2} + 3m + 12\\\frac{{ - 5}}{2} = \frac{3}{2}m - 3 + 3m + 12\\\frac{9}{2}m = - \frac{{23}}{2}\\ \Rightarrow m = - \frac{{23}}{9}\end{array}\)
Vậy \(m = \frac{{ - 23}}{9}\) thì \(\left( {{d_3}} \right):y = \left( {m - 2} \right)x + 3m + 12\) đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
a) Thay x = 0 và y = 100; x = 3600 và y = 87 vào hàm số y = ax + b để xác định a và b.
b) Thay x = 1500 m để tính nhiệt độ sôi của nước ở thành phố này.
a) Thành phố Hồ Chí Minh có độ cao xem như ngang mực nước biển (x = 0m) thì nước có nhiệt độ số là y = \({100^0}C\) nên (0; 100) thuộc đồ thị hàm số y = ax + b => 100 = a.0 + b hay b = 100 => y = ax + 100.
Thủ đô La Paz của Bolivia, Nam Mỹ có độ cao x = 3600 m so với mực nước biển thì nhiệt độ sôi của nước là y = \({87^0}C\) nên (3600; 87) thuộc đồ thị hàm số y = ax + 100 => 87 = a.3600 + 100 => a = \( - \frac{{13}}{{3600}}\).
Do đó \(y = - \frac{{13}}{{3600}}x + 100\).
b) Thành phố Đà Lạt có độ cao 1500 m so với mực nước biển nên x = 1500. Thay x = 1500, ta được:
\(y = - \frac{{13}}{{3600}}.1500 + 100 \approx 95\left( {^0C} \right)\).
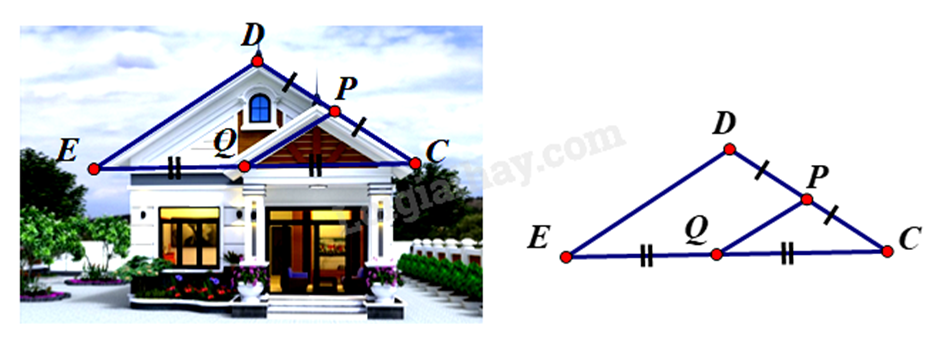
Dựa vào tính chất của đường trung bình để tính.
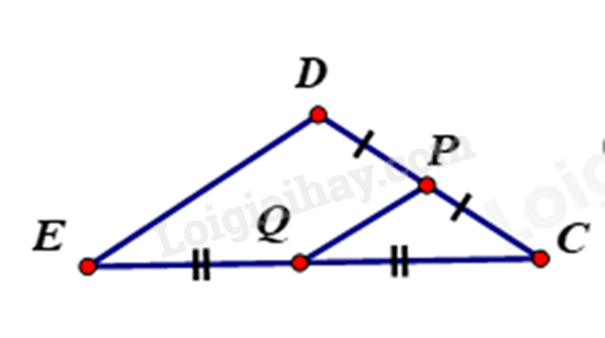
Vì Q là trung điểm EC, P là trung điểm của DC nên PQ là đường trung bình của tam giác CDE.
\(\begin{array}{l} \Rightarrow QP = \frac{1}{2}DE\\ \Rightarrow DE = 2QP = 2.1,5 = 3m\end{array}\)
Vậy chiều dài mái DE bằng 3m.
a) Sử dụng hệ quả của định lí Thales trong tam giác để tính CD.
b) Áp dụng định lí Thales để tính OH.
Sử dụng công thức tính diện tích tam giác.
c) Dựa vào hệ quả và định lí Thales để chứng minh.
d) Chứng minh \(\frac{{AE}}{{AD}} = \frac{{BF}}{{BC}}\) để suy ra \(\frac{{AE}}{{AD}} + \frac{{CF}}{{BC}} = 1\).
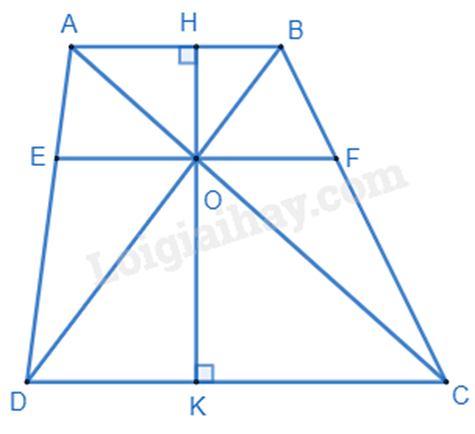
a) Xét tam giác OCD có AB // CD, ta có:
\(\frac{{AO}}{{OC}} = \frac{{AB}}{{CD}}\) (hệ quả của định lí Thales)
\(\frac{4}{8} = \frac{5}{{CD}} \Rightarrow CD = 5:\frac{4}{8} = 10\left( {cm} \right)\)
b) Xét tam giác OKC có AH // KC (vì AB // CD), ta có:
\(\frac{{HO}}{{OK}} = \frac{{OA}}{{OC}}\) (Định lí Thales)
\(\begin{array}{l}\frac{{OH}}{6} = \frac{4}{8} = \frac{1}{2}\\ \Rightarrow OH = \frac{1}{2}.6 = 3\left( {cm} \right)\end{array}\)
\( \Rightarrow {S_{\Delta AOB}} = \frac{1}{2}OH.AB = \frac{1}{2}3.5 = 7,5\left( {c{m^2}} \right)\)
c) Xét tam giác ACD có EO // CD (vì AB // CD) nên \(\frac{{EO}}{{CD}} = \frac{{AO}}{{AC}}\) (hệ quả của định lí Thales)
Xét tam giác BCD có OF // CD (vì AB // CD) nên \(\frac{{BF}}{{BC}} = \frac{{OF}}{{CD}}\) (hệ quả của định lí Thales)
Xét tam giác ABC có OF // AB nên \(\frac{{AO}}{{AC}} = \frac{{BF}}{{BC}}\) (định lí Thales) (1)
\( \Rightarrow \frac{{EO}}{{CD}} = \frac{{OF}}{{CD}} \Rightarrow EO = OF\) (đpcm)
d) Xét tam giác ACD có EO // CD nên \(\frac{{AE}}{{AD}} = \frac{{AO}}{{AC}}\) (2)
Từ (1) và (2) suy ra \(\frac{{AE}}{{AD}} = \frac{{BF}}{{BC}}\)
\( \Rightarrow \frac{{AE}}{{AD}} + \frac{{CF}}{{BC}} = \frac{{BF}}{{BC}} + \frac{{CF}}{{BC}} = \frac{{BF + CF}}{{BC}} = \frac{{BC}}{{BC}} = 1\) (đpcm).
Dựa vào kiến thức về vị trí tương đối của hai đường thẳng.
Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\).
Theo đề bài ta có:
\({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b \ne 2019\end{array} \right. \Rightarrow y = 2x + b\).
Vì \({d_1}\) cắt trục tung tại \(A\left( {0; - 2} \right)\) nên -2 = 2.0 + b \( \Rightarrow \) b = -2 (TM)
\( \Rightarrow {a^2} + {b^3} = {2^2} + {\left( { - 2} \right)^3} = 4 - 8 = - 4\).
Vậy \({a^2} - {b^3} = - 4\).
Phần trắc nghiệm (3 điểm) Câu 1 (150991): Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?
Phần trắc nghiệm (2 điểm) Câu 1: Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\).
Phần trắc nghiệm (2 điểm) Câu 1: Đường trung bình của tam giác: A. Là đoạn thẳng nối hai điểm bất kì trên hai cạnh của tam giác
Phần trắc nghiệm (2 điểm) Câu 1: Chọn khẳng định sai. A. \(y = 6x + 8\) có hệ số của \(x\) là 6 ; hệ số tự do là 8 .
Phần trắc nghiệm (3 điểm) Câu 1: (150980) Câu nào sau đây đúng:
Phần trắc nghiệm (3 điểm) Câu 1: (150976) Cho hàm số $y=f(x)={{x}^{2}}.$ Tính $fleft( -5 right)+fleft( 5 right)$ .
Phần trắc nghiệm (3 điểm) Câu 1: (150973) Cho hàm số $y=f(x)=-{{x}^{2}}+2.$ Tính $fleft( frac{-1}{2} right);fleft( 0 right)$ .
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
