Đề thi giữa kì 2 Toán 8 - Đề số 2 - Chân trời sáng tạo
Phần trắc nghiệm (3 điểm) Câu 1: (150976) Cho hàm số $y=f(x)={{x}^{2}}.$ Tính $fleft( -5 right)+fleft( 5 right)$ .
Đề bài
Cho hàm số \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\) .
-
A.
0.
-
B.
25.
-
C.
50.
-
D.
10.
Thanh long là một loại cây chịu hạn , không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (kg) thanh long ruột đỏ loại I là :
-
A.
y = 32 000.
-
B.
y = 32 000 – x.
-
C.
y = 32 000x.
-
D.
y = 32 000 + x.
Màn hình ra đa của một đài gợi lên hình ảnh một mặt phẳng tọa độ. Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ mấy trong mặt phẳng tọa độ Oxy ?
-
A.
Góc phần tư thứ I.
-
B.
Góc phần tư thứ II.
-
C.
Góc phần tư thứ III.
-
D.
Góc phần tư thứ IV.
-
A.
A(1; 4).
-
B.
B(3; 2).
-
C.
C(2;-2).
-
D.
D(-3;-1).
Hàm số nào sau đây là hàm số bậc nhất?
-
A.
\(y = 2x - 1\).
-
B.
\(y = - {x^2} + 3\).
-
C.
\(y = \frac{1}{x}\).
-
D.
\(y = 2024\).
Hệ số góc của hàm số \(y = - x - 3\) là:
-
A.
1.
-
B.
-1.
-
C.
3.
-
D.
-3.
Viết tỉ số cặp đoạn thằng có độ dài như sau: AB = 4dm; CD = 20dm.
-
A.
\(\frac{{AB}}{{CD}} = \frac{1}{4}\).
-
B.
\(\frac{{AB}}{{CD}} = \frac{1}{5}\).
-
C.
\(\frac{{AB}}{{CD}} = \frac{1}{6}\).
-
D.
\(\frac{{AB}}{{CD}} = \frac{1}{7}\).
-
A.
\(x = \frac{{21}}{5}\).
-
B.
\(x = 2,5\).
-
C.
\(x = 7\).
-
D.
\(x = \frac{{21}}{4}\).
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.
-
A.
\(AB = 3m\).
-
B.
\(AB = 0,75m\).
-
C.
\(AB = 2,4m\).
-
D.
\(AB = 2,25m\).
-
A.
3cm.
-
B.
4,5cm.
-
C.
2,5cm.
-
D.
4cm.
Cho tam giác ABC có P, Q lần lượt là trung điểm của AB và AC. Biết BC = 10cm. Ta có:
-
A.
PQ = 4cm.
-
B.
PQ = 5cm.
-
C.
PQ = 3,5cm.
-
D.
PQ = 10cm.
Cho \(\Delta ABC\), AD là tia phân giác trong của góc A. Hãy chọn câu đúng.
-
A.
\(\frac{{DC}}{{DB}} = \frac{{AB}}{{AC}}\).
-
B.
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\).
-
C.
\(\frac{{AB}}{{DB}} = \frac{{DC}}{{AC}}\).
-
D.
\(\frac{{AD}}{{DB}} = \frac{{AC}}{{AD}}\).
Lời giải và đáp án
Cho hàm số \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\) .
-
A.
0.
-
B.
25.
-
C.
50.
-
D.
10.
Đáp án : C
Thay x = -5; x = 5 vào hàm số.
Tính \(f\left( { - 5} \right) + f\left( 5 \right)\).
Ta có:
\(\begin{array}{l}f\left( { - 5} \right) = {\left( { - 5} \right)^2} = 25\\f\left( 5 \right) = {5^2} = 25\\ \Rightarrow f\left( { - 5} \right) + f\left( 5 \right) = 25 + 25 = 50\end{array}\)
Thanh long là một loại cây chịu hạn , không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (kg) thanh long ruột đỏ loại I là :
-
A.
y = 32 000.
-
B.
y = 32 000 – x.
-
C.
y = 32 000x.
-
D.
y = 32 000 + x.
Đáp án : C
Biểu thị y theo x.
Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng nên giá bán x (kg) thanh long là: 32 000.x (đồng).
Vậy ta có công thức biểu thị là y = 32 000x.
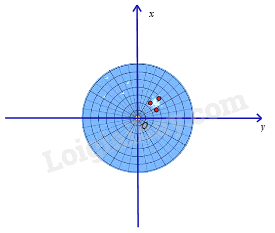
Màn hình ra đa của một đài gợi lên hình ảnh một mặt phẳng tọa độ. Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ mấy trong mặt phẳng tọa độ Oxy ?
-
A.
Góc phần tư thứ I.
-
B.
Góc phần tư thứ II.
-
C.
Góc phần tư thứ III.
-
D.
Góc phần tư thứ IV.
Đáp án : A
Dựa vào kiến thức về các góc phần tư.
Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ I.
-
A.
A(1; 4).
-
B.
B(3; 2).
-
C.
C(2;-2).
-
D.
D(-3;-1).
Đáp án : D
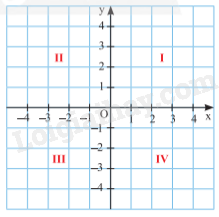
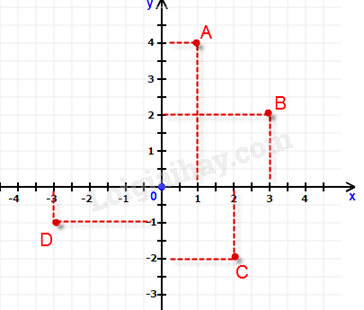
Quan sát hình vẽ để xác định tọa độ các điểm.
Hình chiếu của điểm A trên trục hoành là 1, trên trục tung là 4 nên tọa độ điểm A là A(1; 4). => A đúng.
Hình chiếu của điểm B trên trục hoành là 3, trên trục tung là 2 nên tọa độ điểm B là B(3; 2). => B đúng.
Hình chiếu của điểm C trên trục hoành là 2, trên trục tung là -2 nên tọa độ điểm C là C(2;-2). => C đúng.
Hình chiếu của điểm D trên trục hoành là -3, trên trục tung là 1 nên tọa độ điểm D là C(-3;1). => D sai.
Hàm số nào sau đây là hàm số bậc nhất?
-
A.
\(y = 2x - 1\).
-
B.
\(y = - {x^2} + 3\).
-
C.
\(y = \frac{1}{x}\).
-
D.
\(y = 2024\).
Đáp án : A
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Hàm số \(y = 2x - 1\) là hàm số bậc nhất vì có dạng \(y = ax + b\) và hệ số \(a = 2 \ne 0\).
Hàm số \(y = - {x^2} + 3\) không là hàm số bậc nhất vì có \({x^2}\).
Hàm số \(y = \frac{1}{x}\) không là hàm số bậc nhất vì có x nằm ở mẫu.
Hàm số \(y = 2024\) không là hàm số bậc nhất vì hệ số \(a = 0\).
Hệ số góc của hàm số \(y = - x - 3\) là:
-
A.
1.
-
B.
-1.
-
C.
3.
-
D.
-3.
Đáp án : B
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\) với a là hệ số góc.
Hệ số góc của hàm số \(y = - x - 3\) là a = -1.
Viết tỉ số cặp đoạn thằng có độ dài như sau: AB = 4dm; CD = 20dm.
-
A.
\(\frac{{AB}}{{CD}} = \frac{1}{4}\).
-
B.
\(\frac{{AB}}{{CD}} = \frac{1}{5}\).
-
C.
\(\frac{{AB}}{{CD}} = \frac{1}{6}\).
-
D.
\(\frac{{AB}}{{CD}} = \frac{1}{7}\).
Đáp án : B
Sử dụng kiến thức về tỉ số của hai đoạn thẳng.
Ta có: \(\frac{{AB}}{{CD}} = \frac{4}{{20}} = \frac{1}{5}\).
-
A.
\(x = \frac{{21}}{5}\).
-
B.
\(x = 2,5\).
-
C.
\(x = 7\).
-
D.
\(x = \frac{{21}}{4}\).
Đáp án : A
Áp dụng định lí Thalès để tính x.
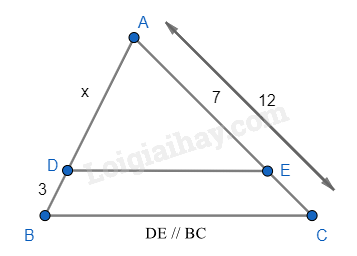
Vì DE // BC nên \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} \Leftrightarrow \frac{x}{{x + 3}} = \frac{7}{{12}}\)
\(\begin{array}{l} \Leftrightarrow 12x = 7\left( {x + 3} \right) \Leftrightarrow 12x = 7x + 21\\ \Leftrightarrow 12x - 7x = 21 \Leftrightarrow 5x = 21 \Leftrightarrow x = \frac{{21}}{5}\end{array}\)
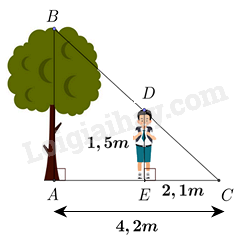
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.
-
A.
\(AB = 3m\).
-
B.
\(AB = 0,75m\).
-
C.
\(AB = 2,4m\).
-
D.
\(AB = 2,25m\).
Đáp án : A
Dựa vào hệ quả của định lí Thales trong tam giác.
Vì cái cây và người đều vuông góc với mặt đất nên AB // DE.
Áp dụng hệ quả của định lí Thales vào tam giác ABC có DE // AB, ta có:
\(\frac{{CE}}{{AC}} = \frac{{DE}}{{AB}}\)
\(\frac{{2,1}}{{4,2}} = \frac{{1,5}}{{AB}} \Rightarrow AB = 1,5:\frac{{2,1}}{{4,2}} = 3\left( m \right)\)
-
A.
3cm.
-
B.
4,5cm.
-
C.
2,5cm.
-
D.
4cm.
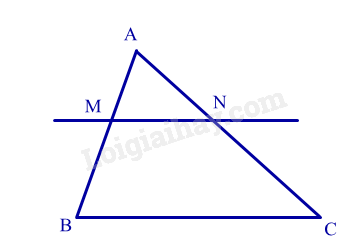
Đáp án : B
Dựa vào định lí Thales trong tam giác.
Áp dụng định lí Thales vào tam giác ABC có MN // BC, ta có:
\(\begin{array}{l}\frac{{AM}}{{BM}} = \frac{{AN}}{{NC}}\\\frac{2}{3} = \frac{3}{{NC}} \Rightarrow NC = 3:\frac{2}{3} = 4,5\left( {cm} \right)\end{array}\)
Cho tam giác ABC có P, Q lần lượt là trung điểm của AB và AC. Biết BC = 10cm. Ta có:
-
A.
PQ = 4cm.
-
B.
PQ = 5cm.
-
C.
PQ = 3,5cm.
-
D.
PQ = 10cm.
Đáp án : B
Dựa vào tính chất của đường trung bình.
Xét tam giác ABC có P, Q lần lượt là trung điểm của AB và AC nên PQ là đường trung bình của tam giác ABC \( \Rightarrow PQ = \frac{1}{2}BC = \frac{1}{2}.10 = 5\left( {cm} \right)\).
Cho \(\Delta ABC\), AD là tia phân giác trong của góc A. Hãy chọn câu đúng.
-
A.
\(\frac{{DC}}{{DB}} = \frac{{AB}}{{AC}}\).
-
B.
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\).
-
C.
\(\frac{{AB}}{{DB}} = \frac{{DC}}{{AC}}\).
-
D.
\(\frac{{AD}}{{DB}} = \frac{{AC}}{{AD}}\).
Đáp án : B
Sử dụng tính chất của đường phân giác trong tam giác.
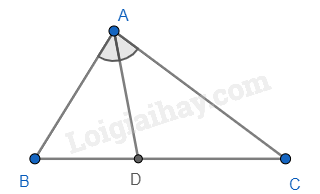
Theo tính chất của đường phân giác trong tam giác, ta có: \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\) nên B đúng.
a) Thay tọa độ của A, B vào hàm số để chứng minh.
b) Dựa vào các bước xác định một điểm với tọa độ cho trước trên mặt phẳng.
c) Điểm nằm trên trục hoành có tung độ bằng 0. Thay y = 0 vào để tìm hoành độ của C.
a) Ta có: \( - 2.0 + 1 = 1 \Rightarrow A\left( {0;1} \right)\) thuộc đồ thị của hàm số (1) (đpcm)
\( - 2.\frac{3}{2} + 1 = - 3 + 1 = - 2 \Rightarrow B\left( {\frac{3}{2}; - 2} \right)\) thuộc đồ thị của hàm số (1) (đpcm).
b) Biểu diễn A trong mặt phẳng tọa độ Oxy:
- Điểm A có hoành độ bằng 0 nên nằm trên trục tung.
- Trên trục tung lấy điểm 1 ta được điểm \(A\left( {0;1} \right)\).
Biểu diễn B trong mặt phẳng tọa độ Oxy.
- Trên trục hoành lấy điểm \(\frac{3}{2}\), vẽ đường thẳng vuông góc với trục hoành tại điểm \(\frac{3}{2}\).
- Trên trục tung lấy điểm \( - 2\), vẽ đường thẳng vuông góc với trục tung tại điểm \( - 2\).
- Giao điểm của hai đường thẳng vừa vẽ là điểm B cần tìm.
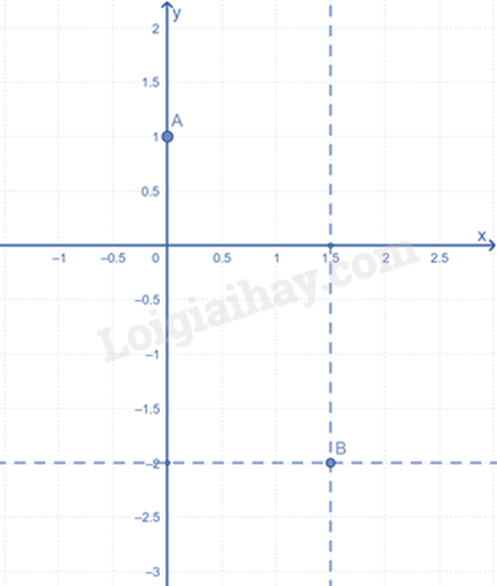
c) Điểm C nằm trên trục hoành nên có tung độ bằng 0.
Điểm C thuộc đồ thị của hàm số (1) nên ta có:
\(\begin{array}{l} - 2{x_C} + 1 = 0\\{x_C} = \frac{1}{2}\end{array}\)
Vậy tọa độ điểm C là \(C\left( {\frac{1}{2};0} \right)\).
a) Dựa vào các dữ kiện đề bài cho để viết hàm số. Kiểm tra xem y có dạng \(y = ax + b\left( {a \ne 0} \right)\) không.
b) Thay x = 150 để tính số tiền.
a) Số tiền in đĩa gốc là 10 triệu đồng và số tiền in mỗi đĩa in sao là 60 000 nên nếu in x đĩa in sao và một đĩa gốc thì số tiền là: y = 60 000.x + 10 000 000
Vì hàm số y có dạng y = ax + b với a = 60 000 \( \ne \) 0 nên y là hàm số bậc nhất.
b) Để in được 150 đĩa sao và một đĩa gốc thì các bạn khối 8 cần góp số tiền là:
y = 60 000.150 + 10 000 000 = 19 000 000 (đồng)
Vậy các bạn khối 8 cần góp 19 000 000 đồng để in được 150 đĩa sao và một đĩa gốc.
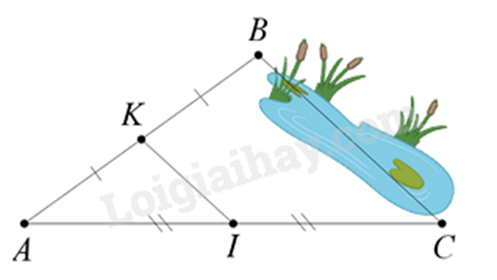
Dựa vào tính chất đường trung bình trong tam giác.
Vì K là trung điểm của AB, I là trung điểm của AC nên KI là đường trung bình của tam giác ABC
=> KI // BC và KI = \(\frac{1}{2}\)BC.
Vì KI = 30 m nên BC = 2.KI = 2.30 = 60 m.
Vậy BC = 60 m.
a) Chứng minh tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Chứng minh AO là đường trung bình của tam giác BED nên \(AO = \frac{1}{2}ED\).
Mà O là trung điểm của AC nên \(AO = \frac{1}{2}AC \Rightarrow AC = DE\).
c) Áp dụng tính chất của đường phân giác và định lí Thales đảo để chứng minh MN // AC.
Gọi F là giao điểm của BO và MN.
Dựa vào hệ quả của định lí Thales để suy ra MF = FN để được đpcm.
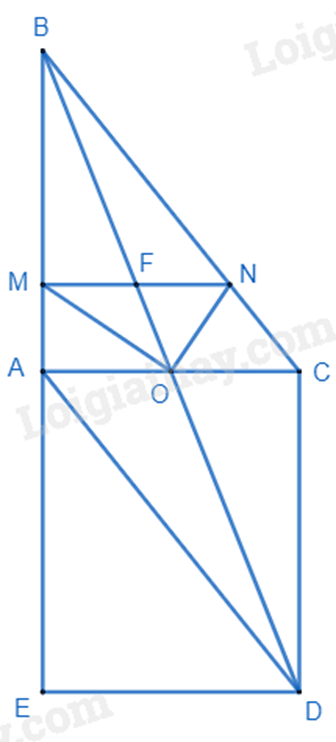
a) Xét tứ giác ABCD có:
O là trung điểm của AC
O là trung điểm của BD.
\(AC \cap BD = O\)
\( \Rightarrow \) ABCD là hình bình hành. (đpcm)
b) Xét tam giác BED có:
A là trung điểm của BE
O là trung điểm của BD
\( \Rightarrow \) AO là đường trung bình của tam giác BED.
\( \Rightarrow AO = \frac{1}{2}ED\)
Mà \(AO = \frac{1}{2}AC\) (O là trung điểm của AC)
\( \Rightarrow AC = ED\) (đpcm)
c) Áp dụng tính chất của đường phân giác, ta có:
OM là tia phân giác của \(\widehat {AOB}\) \( \Rightarrow \frac{{AO}}{{AM}} = \frac{{OB}}{{BM}} \Rightarrow \frac{{AO}}{{OB}} = \frac{{AM}}{{BM}}\)
ON là tia phân giác của \(\widehat {BOC}\) \( \Rightarrow \frac{{OC}}{{CN}} = \frac{{OB}}{{BN}} \Rightarrow \frac{{OC}}{{OB}} = \frac{{CN}}{{BN}}\)
Mà \(AO = OC\) (gt)
\( \Rightarrow \frac{{AM}}{{BM}} = \frac{{CN}}{{BN}}\)\( \Rightarrow MN//AC\) (định lí Thales đảo) (đpcm)
Gọi F là giao điểm của MN và BO.
Vì MN // AC nên áp dụng hệ quả của định lí Thales vào:
\(\Delta AOB\) có: \(\frac{{BF}}{{BO}} = \frac{{MF}}{{AO}}\)
\(\Delta BOC\) có: \(\frac{{BF}}{{BO}} = \frac{{NF}}{{OC}}\)
\( \Rightarrow \frac{{MF}}{{AO}} = \frac{{NF}}{{OC}} \Rightarrow \frac{{MF}}{{NF}} = \frac{{AO}}{{OC}} = 1 \Rightarrow MF = NF\) hay F là trung điểm của MN \( \Rightarrow \) BO đi qua trung điểm của MN. (đpcm)
Tìm tọa độ giao điểm của đường thẳng với hai trục tọa độ.
Tìm điều kiện để có hai tam giác cân.
Giải phương tình để tìm m.
Ta có: \(d \cap Oy = \left\{ B \right\}\)
\({x_B} = 0 \Rightarrow {y_B} = m - 1\)\( \Rightarrow B\left( {0;m - 1} \right)\)\( \Rightarrow OB = \left| {m - 1} \right|\).
\({y_A} = 0 \Leftrightarrow m{x_A} + m - 1 = 0 \Leftrightarrow {x_A} = \frac{{1 - m}}{m}\left( {m \ne 0} \right)\)\( \Rightarrow A\left( {\frac{{1 - m}}{m};0} \right)\)\( \Rightarrow OA = \left| {\frac{{1 - m}}{m}} \right|\).
Vì tam giác AOB vuông cân tại O nên:
\(\begin{array}{l}OA = OB\\\left| {m - 1} \right| = \left| {\frac{{1 - m}}{m}} \right|\\\left[ \begin{array}{l}m - 1 = \frac{{1 - m}}{m}\\m - 1 = - \frac{{1 - m}}{m}\end{array} \right.\\\left[ \begin{array}{l}{m^2} = 1\\\left( {m - 1} \right)\left( {1 - \frac{1}{m}} \right) = 0\end{array} \right.\\\left[ \begin{array}{l}m = \pm 1\\m = 1\end{array} \right.\\m = \pm 1\left( {TM} \right)\end{array}\)
Vậy \(m = \pm 1\) thì tam giác AOB vuông cân.
Phần trắc nghiệm (3 điểm) Câu 1: (150980) Câu nào sau đây đúng:
Câu 1: (150984) Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng
Phần trắc nghiệm (3 điểm) Câu 1 (150991): Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?
Phần trắc nghiệm (2 điểm) Câu 1: Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\).
Phần trắc nghiệm (2 điểm) Câu 1: Đường trung bình của tam giác: A. Là đoạn thẳng nối hai điểm bất kì trên hai cạnh của tam giác
Phần trắc nghiệm (2 điểm) Câu 1: Chọn khẳng định sai. A. \(y = 6x + 8\) có hệ số của \(x\) là 6 ; hệ số tự do là 8 .
Phần trắc nghiệm (3 điểm) Câu 1: (150973) Cho hàm số $y=f(x)=-{{x}^{2}}+2.$ Tính $fleft( frac{-1}{2} right);fleft( 0 right)$ .
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
