Để đo chiều cao AC của một cột cờ (như hình vẽ), người ta cắm một cái cọc ED có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại B, biết khoảng cách BE là 1,5m và khoảng cách AB là 9m.

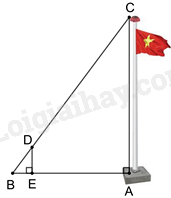
Khi đó chiều cao AC của cột cờ là:

Trong các hàm số sau hàm số có hệ số góc dương là:

Nếu \(P\left( {1; - 2} \right)\) thuộc đường thẳng \(x - y = m\) thì m bằng:

Cho hình vẽ dưới đây, biết AB // DE. Giá trị của x là:

Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Gọi P, Q lần lượt là trung điểm của AB, AC. Khi đó độ dài PQ là:

Cho \(\left( {{d_1}} \right):y = x - 4\) và \(\left( {{d_2}} \right):y =  - 3x + 2\).

a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một hệ trục tọa độ.

b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).

c) Tìm m để \(\left( {{d_3}} \right):y = \left( {m - 2} \right)x + 3m + 12\) đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).

Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?

Cho hình thang ABCD (AB // CD). Gọi giao điểm hai đường chéo AC và BD là O. Biết OA = 4cm; OC = 8cm; AB = 5cm.

a) Tính CD.

b) Qua O kẻ đường thẳng vuông góc với AB và CD lần lượt tại H và K. Tính diện tích tam giác AOB, biết OK = 6cm.

c) Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại E và F. Chứng minh rằng \(OE = OF\).

d) Chứng minh rằng \(\frac{{AE}}{{AD}} + \frac{{CF}}{{BC}} = 1\).

Cho đường thẳng \(\left( {{d_1}} \right):y = ax + b\) song song với đường thẳng \(\left( {{d_2}} \right):y = 2x + 2019\) và cắt trục tung tại điểm \(A\left( {0; - 2} \right)\). Tính giá trị của biểu thức \({a^2} + {b^3}\)?