25 bài tập ứng dụng tích phân trong hình học mức độ thông hiểu
Làm đề thiCâu hỏi 1 :
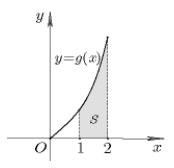
Cho hàm số \(y = f\left( x \right)\) liên tục trên R và hàm số \(y = g\left( x \right) = x.f\left( {{x^2}} \right)\) có đồ thị trên đoạn \(\left[ {0;2} \right]\) như hình vẽ bên. Biết diện tích miền được tô màu là \(S = {5 \over 8},\) tính tích phân \(I = \int\limits_1^4 {f\left( x \right){\rm{d}}x} .\)
- A \(I = {5 \over 4}.\)
- B \(I = {5 \over 2}.\)
- C \(I = 5.\)
- D \(I = 10.\)
Đáp án: A
Phương pháp giải:
Dựa vào hình vẽ suy ra diện tích hình phẳng tô đậm theo g(x).
Sử dụng phương pháp đổi biến để tính tích phân I.
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy rằng \(S = \int\limits_1^2 {\left| {g\left( x \right)} \right|{\rm{d}}x} \) vì \(g\left( x \right) \ge 0,\,\,\forall x \in \left[ {1;2} \right] \Rightarrow S = \int\limits_1^2 {g\left( x \right){\rm{d}}x} = {5 \over 8}\)
Khi đó \(S = \int\limits_1^2 {x.f\left( {{x^2}} \right){\rm{d}}x} .\) Đặt \(t = {x^2} \Leftrightarrow {\rm{d}}t = 2x\,{\rm{d}}x \Leftrightarrow x\,{\rm{d}}x = {{{\rm{d}}t} \over 2}\) và đổi cận \(\left\{ \matrix{ x = 1\,\, \Rightarrow \,\,t = 1 \hfill \cr x = 2\,\, \Rightarrow \,\,t = 4 \hfill \cr} \right..\)
Vậy \(S = {5 \over 8} \Leftrightarrow \int\limits_1^4 {{1 \over 2}.f\left( t \right){\rm{d}}t} = {5 \over 8} \Leftrightarrow {1 \over 2}.\int\limits_1^4 {f\left( t \right){\rm{d}}t} = {5 \over 8} \Leftrightarrow \int\limits_1^4 {f\left( x \right){\rm{d}}x} = {5 \over 4}\,\,\buildrel {} \over \longrightarrow \,I = {5 \over 4}.\)
Chọn A.
Câu hỏi 2 :
Diện tích hình phẳng giới hạn bởi \(y = {{\sqrt {1 + \ln x} } \over x}; x = 1; x = e\) và trục hoành là \(S\) được biểu diễn dưới dạng \(S = {{a + 4\sqrt 2 } \over b},\) với \(a,\,\,b \in Q\) Tính tổng \(T = a + 2b.\)
- A \(T = - \,1.\)
- B \(T = 0.\)
- C \(T = 4.\)
- D \(T = 2.\)
Đáp án: C
Phương pháp giải:
Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \)
Đồng nhất hệ số, tìm a, b và tính tổng.
Lời giải chi tiết:
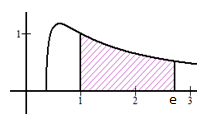
Do \({{\sqrt {1 + \ln x} } \over x} \ge 0;\,\,\forall x \in \left[ {1;\,\,e} \right] \Rightarrow \left| {{{\sqrt {1 + \ln x} } \over x}} \right| = {{\sqrt {1 + \ln x} } \over x}\), suy ra diện tích cần xác định là
\(S = \int\limits_1^e {\left| {{{\sqrt {1 + \ln x} } \over x}} \right|{\rm{d}}x} = \int\limits_1^e {{{\sqrt {1 + \ln x} } \over x}{\rm{d}}x} \).
Đặt \(t = \sqrt {1 + \ln x} \Rightarrow {t^2} = 1 + \ln x \Rightarrow 2t\,{\rm{d}}t = {{{\rm{d}}x} \over x}.\)
Khi \(\left\{ \matrix{ x = e\,\, \Rightarrow \,\,t = \sqrt 2 \hfill \cr x = 1\, \Rightarrow t = 1 \hfill \cr} \right..\) Vậy \(S = \int\limits_1^{\sqrt 2 } {t.2t\,{\rm{d}}t} = \int\limits_1^{\sqrt 2 } {2{t^2}\,{\rm{d}}t} = \left. {{2 \over 3}{t^3}} \right|_1^{\sqrt 2 } = {{4\sqrt 2 - 2} \over 3} = {{a + 4\sqrt 2 } \over b} \Rightarrow \left\{ \matrix{ a = - \,2 \hfill \cr b = 3 \hfill \cr} \right..\)
Vậy tổng \(T = a + 2b = - \,2 + 2.3 = 4.\)
Chọn C.
Câu hỏi 3 :
Diện tích hình phẳng giới hạn bởi \(y = x\left( {x + 1} \right)\left( {x - 2} \right); x = - \,2; x = 2\) và trục hoành là \(S = {a \over b},\) với \(a,\,\,b > 0\) và \({a \over b}\) là phân số tối giản. Tính giá trị của biểu thức \(P = a - 5b.\)
- A \(P = 5.\)
- B \(P = 0\)
- C \(P = -1\)
- D \(P = 7\)
Đáp án: D
Phương pháp giải:
Giải phương trình hoành độ giao điểm, tím các nghiệm thuộc [-2; 2].
Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \)
Chia nhỏ tích phân cần tính thành các đoạn mà trên các đoạn đó dấu của f(x) là xác định.
Lời giải chi tiết:
Phương trình hoành độ giao điểm của \(\left( C \right)\) với \(Ox\) là \(x\left( {x + 1} \right)\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \matrix{ x = - \,1 \hfill \cr x = 0 \hfill \cr x = 2 \hfill \cr} \right..\)
Vậy diện tích cần tính là
\(\eqalign{ & S = \int\limits_{ - 2}^2 {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} = \int\limits_{ - 2}^{ - 1} {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} + \int\limits_{ - 1}^0 {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} + \int\limits_0^2 {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} \cr & = \left| {\int\limits_{ - \,2}^{ - \,1} {\left( {{x^3} - {x^2} - 2x} \right){\rm{d}}x} } \right| + \left| {\int\limits_{ - \,1}^0 {\left( {{x^3} - {x^2} - 2x} \right){\rm{d}}x} } \right| + \left| {\int\limits_0^2 {\left( {{x^3} - {x^2} - 2x} \right){\rm{d}}x} } \right| \cr & = \left| {\left. {\left( {{{{x^4}} \over 4} - {{{x^3}} \over 3} - {x^2}} \right)} \right|_{ - 2}^{ - 1}} \right| + \left| {\left. {\left( {{{{x^4}} \over 4} - {{{x^3}} \over 3} - {x^2}} \right)} \right|_{ - 1}^0} \right| + \left| {\left. {\left( {{{{x^4}} \over 4} - {{{x^3}} \over 3} - {x^2}} \right)} \right|_0^2} \right| \cr & = \left| { - {5 \over {12}} - {8 \over 3}} \right| + \left| {0 + {5 \over {12}}} \right| + \left| { - {8 \over 3}} \right| = {{37} \over 6} = {a \over b} \Rightarrow \left\{ \matrix{ a = 37 \hfill \cr b = 6 \hfill \cr} \right. \Rightarrow P = 7. \cr} \)
Chọn D.
Câu hỏi 4 :
Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số \(y = {{\ln x} \over {\sqrt x }},\) trục hoành, đường thẳng \(x = 1\) và đường thẳng \(x = e\) bằng \(ae + b.\) Khi đó \({a^2}\) gần với giá trị nào nhất ?
- A \(\sqrt 2 .\)
- B \(\sqrt 3\)
- C \(2\sqrt 2\)
- D \(2\sqrt 3\)
Đáp án: A
Phương pháp giải:
Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \)
Lời giải chi tiết:
Ta có \(S = \int\limits_1^e {\left| {{{\ln x} \over {\sqrt x }}} \right|{\rm{d}}x} = \int\limits_1^e {{{\ln x} \over {\sqrt x }}{\rm{d}}x} .\) (Vì với \(x \in \left[ {1;e} \right] \Rightarrow \ln 1 < \ln x < \ln e \Rightarrow \ln x > 0\))
Đặt
\(\eqalign{ & \left\{ \matrix{ u = \ln x \hfill \cr dv = {{dx} \over {\sqrt x }} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ du = {{dx} \over x} \hfill \cr v = 2\sqrt x \hfill \cr} \right. \Rightarrow \int\limits_1^e {{{\ln x} \over {\sqrt x }}{\rm{d}}x} = \left. {\ln x.2\sqrt x } \right|_1^e - 2\int\limits_1^e {{{dx} \over {\sqrt x }}} = \left. {\left( {\ln x.2\sqrt x - 4\sqrt x } \right)} \right|_1^e = - 2\sqrt e + 4 = - {2 \over {\sqrt e }}e + 4 \cr & \int\limits_1^e {{{\ln x} \over {\sqrt x }}{\rm{d}}x} = ae + b \Rightarrow \left\{ \matrix{ a = - {2 \over {\sqrt e }} \hfill \cr b = 4 \hfill \cr} \right. \Rightarrow {a^2} = {4 \over e} \approx 1,4715 \approx \sqrt 2 . \cr} \)
Chọn A.
Câu hỏi 5 :
Thể tích khối tròn xoay sinh ra bởi phép quay xung quanh \(Ox\) của hình giới hạn bởi trục \(Ox\) và parabol \(\left( P \right):y={{x}^{2}}-ax\,\,\,\,\left( a>0 \right)\) bằng \(V=2.\) Khẳng định nào dưới đây đúng ?
- A \(a\in \left( \frac{1}{2};1 \right).\)
- B \(a\in \left( 1;\frac{3}{2} \right).\)
- C \(a\in \left( \frac{3}{2};2 \right).\)
- D \(a\in \left( 2;\frac{5}{2} \right).\)
Đáp án: C
Phương pháp giải:
Xét phương trình hoành độ giao điểm của (P) và trục Ox, tìm ra các cận x = a và x = b.
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\)
Lời giải chi tiết:
Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(Ox\) là \({{x}^{2}}-ax=0\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=a \\\end{align} \right..\)
Khi đó, thể tích cần xác định cho bởi \(V=\pi \int\limits_{0}^{a}{{{\left( {{x}^{2}}-ax \right)}^{2}}\text{d}x}=\pi \int\limits_{0}^{a}{\left( {{x}^{4}}-2a{{x}^{3}}+{{a}^{2}}{{x}^{2}} \right)\text{d}x}\)
\(=\pi \left. \left( \frac{{{x}^{5}}}{5}-\frac{a{{x}^{4}}}{2}+\frac{{{a}^{2}}{{x}^{3}}}{3} \right) \right|_{0}^{a}=\frac{\pi {{a}^{5}}}{30}.\) Mặt khác \(V=2\Rightarrow \frac{\pi {{a}^{5}}}{30}=2\Leftrightarrow a=\sqrt[5]{{\frac{{60}}{\pi }}}\in \left( \frac{3}{2};2 \right).\)
Chọn C.
Câu hỏi 6 :
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y=\sqrt{x}\), \(y=-\,x\) và \(x=4.\) Thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục hoành là \(V=\frac{a\pi }{b},\) với \(a,\,\,b>0\) và \(\frac{a}{b}\) là phân số tối giản. Tính tổng \(T=a+b.\)
- A \(T=44.\)
- B \(T=36.\)
- C \(T=50.\)
- D \(T=24.\)
Đáp án: A
Phương pháp giải:
Xét phương trình hoành độ giao điểm.
Áp dụng công thức tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\)
Đưa tích phân cần tính về dạng \(V=\frac{a\pi }{b},\) và tìm ra các hệ số a và b, thay vào tính tổng a + b.
Lời giải chi tiết:
Phương trình hoành độ giao điểm của \(y=\sqrt{x},\,\,y=-\,x\) là \(\sqrt{x}=-\,x\Leftrightarrow x=0.\)
Khi đó, thể tích cần tính là \(V=\pi \int\limits_{0}^{4}{\left| {{\left( \sqrt{x} \right)}^{2}}-{{\left( -\,x \right)}^{2}} \right|\text{d}x}=\pi \int\limits_{0}^{4}{\left| x-{{x}^{2}} \right|\text{d}x}\)
\(=\pi \int\limits_{1}^{4}{\left| x-{{x}^{2}} \right|\text{d}x}+\pi \int\limits_{0}^{1}{\left| x-{{x}^{2}} \right|\text{d}x}=\pi \int\limits_{1}^{4}{\left( {{x}^{2}}-x \right)\text{d}x}+\pi \int\limits_{0}^{1}{\left( x-{{x}^{2}} \right)\text{d}x}\)
\( = \pi \left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)\left| \begin{array}{l}^4\\_1\end{array} \right. + \pi \left( {\frac{{{x^2}}}{2} - \frac{{{x^3}}}{3}} \right)\left| \begin{array}{l}^1\\_0\end{array} \right. = \frac{{41\pi }}{3} = \frac{{a\pi }}{b}\,\, \Rightarrow \,\,\left\{ \begin{array}{l}a = 41\\b = 3\end{array} \right..\)
Vậy \(T=44.\)
Chọn A.
Câu hỏi 7 :
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y=-\,{{x}^{2}}+2x\) và \(y=0\). Tính thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục Oy là:
- A \(V=\frac{7}{3}\pi .\)
- B \(V=\frac{8}{3}\pi .\)
- C \(V=\frac{10}{3}\pi .\)
- D \(V=\frac{16}{3}\pi .\)
Đáp án: B
Phương pháp giải:
Rút hàm số theo biến y, \(x=f\left( y \right);x=g\left( y \right)\).
Giải phương trình tung độ giao điểm để tìm ra các cận y = a và y = b.
Áp dụng công thức tính thể tích khối tròn khi xoay quanh trục Oy của hình phẳng bị giới hạn bởi đồ thị các hàm số \(x=f\left( y \right),x=g\left( y \right),y=a,y=b\) là \(V=\int\limits_{a}^{b}{\left| {{f}^{2}}\left( y \right)-{{g}^{2}}\left( y \right) \right|dy}\).
Lời giải chi tiết:
Ta có \(y=-\,{{x}^{2}}+2x\Rightarrow {{\left( x-1 \right)}^{2}}=1-y\Rightarrow \left[ \begin{align} & \text{ }x=1-\sqrt{1-y} \\ & \text{ }x=1+\sqrt{1-y} \\ \end{align} \right..\)
Xét phương trình tung độ giao điểm \(1-\sqrt{1-y}=1+\sqrt{1-y}\Leftrightarrow \sqrt{1-y}=0\Leftrightarrow y=1\).
Khi đó, thể tích cần tính là \(V=\pi \int\limits_{0}^{1}{\left| {{\left( 1+\sqrt{1-y} \right)}^{2}}-{{\left( 1-\sqrt{1-y} \right)}^{2}} \right|\text{d}y}=\left| \pi \int\limits_{0}^{1}{4\sqrt{1-y}\,\text{d}y} \right|\)
Đặt \(\sqrt{1-y}=t\Leftrightarrow 1-y={{t}^{2}}\Leftrightarrow dy=-2tdt\)
Đổi cận: \(\left\{ \begin{align} & y=0\Leftrightarrow t=1 \\ & y=1\Leftrightarrow t=0 \\ \end{align} \right.\)
Khi đó \(V=\left| -\pi \int\limits_{1}^{0}{4t.2tdt} \right|=\left| 8\pi \int\limits_{0}^{1}{{{t}^{2}}dt} \right|=\left| 8\left. \pi \frac{{{t}^{3}}}{3} \right|_{0}^{1} \right|=\frac{8\pi }{3}\)
Chọn B.
Câu hỏi 8 :
Thể tích của khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi \(\left( C \right):y=\ln x,\) trục Ox và đường thẳng \(x=e\) có dạng \(\pi \left( e-a \right)\). Khi đó a bằng:
- A 2
- B 1
- C 0
- D -1
Đáp án: A
Phương pháp giải:
Giải phương trình hoành độ giao điểm để tìm các cận.
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\)
Lời giải chi tiết:
Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(Ox\) là \(\ln x=0\Leftrightarrow x=1.\)
Khi đó, thể tích cần tính là \(V=\pi \int\limits_{1}^{e}{{{\ln }^{2}}x\,\text{d}x}=\pi \left( x{{\ln }^{2}}x \right)\left| \begin{align} & ^{e} \\ & _{1} \\\end{align} \right.-\pi \int\limits_{1}^{e}{x\,\text{d}\left( {{\ln }^{2}}x \right)}.\)
Đặt
\(\left\{ \begin{array}{l}u = {\ln ^2}x\\dv = dx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}du = 2\frac{{\ln x}}{x}dx\\v = x\end{array} \right. \Rightarrow V = \pi \left[ {\left. {x{{\ln }^2}x} \right|_1^e - 2\int\limits_1^e {\ln xdx} } \right] = \pi \left[ {e - 2\int\limits_1^e {\ln xdx} } \right]\)
Đặt
\(\left\{ \begin{array}{l}u = \ln x\\dv = dx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}du = \frac{{dx}}{x}\\v = x\end{array} \right. \Leftrightarrow \int\limits_1^e {\ln xdx} = \left. {x\ln x} \right|_1^e - \int\limits_1^e {dx} = \left. {x\ln x} \right|_1^e - \left. x \right|_1^e = e - e + 1 = 1\)
Vậy \(I=\pi \left( e-2 \right)\Rightarrow a=2\)
Chọn A.
Câu hỏi 9 :
Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau: Họ tiến hành quan sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc \(15 m/s\). Hỏi biểu thức vận tốc của tia lửa điện là:
- A \(v = -9,8t + 15\)
- B \(v= -9,8t + 13\)
- C \(v = 9,8t + 15\)
- D \(v = -9,8t – 13\)
Đáp án: A
Phương pháp giải:
+) Tia lửa điện của trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\)
+) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \)
+) Sử dụng giả thiết v(0) = 15 để tìm hằng số C.
Lời giải chi tiết:
Tia lửa điện của trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\)
Ta có biểu thức vận tốc theo thời gian t là \(v\left( t \right) = \int {a\left( t \right)dt} = \int { - 9,8dt} = - 9,8t + C\)
Mà \(v\left( 0 \right) = 15 \Rightarrow C = 15 \Rightarrow v = - 9,8t + 15\)
Chọn A.
Câu hỏi 10 :
Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau: Họ tiến hành quan sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc 15 m/s. Hỏi sau 2,5 giây thì tia lửa điện có chiều cao là bao nhiêu?
- A \(6,235m\)
- B \(5,635m\)
- C \(4,235m\)
- D \(6,875m\)
Đáp án: D
Phương pháp giải:
+) Tia lửa điện có trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\)
+) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \)
+) Sử dụng giả thiết v(0) = 15 để tìm hằng số C.
+) Sử dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \)
Lời giải chi tiết:
Tia lửa điện có trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\)
Ta có biểu thức vận tốc theo thời gian t là \(v\left( t \right) = \int {a\left( t \right)dt} = \int { - 9,8dt} = - 9,8t + C\)
Mà \(v\left( 0 \right) = 15 \Rightarrow C = 15 \Rightarrow v = - 9,8t + 15\)
Vậy sau 2,5 giây thì tia lửa điện có chiều cao là \(S = \int\limits_0^{2,5} {\left( { - 9,8t + 15} \right)dt} = 6,875\,\,\left( m \right)\)
Chọn D.
Câu hỏi 11 :
Một vật chuyển động với gia tốc \(a\left( t \right) = - 20{\left( {1 + 2t} \right)^{ - 2}}\,\,\left( {m/{s^2}} \right)\). Khi t = 0 thì vận tốc của vật là 30 m/s. Tính quãng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).
- A \(S = 46m\)
- B \( S = 47m\)
- C \(S = 48m\)
- D \(S = 49m\)
Đáp án: C
Phương pháp giải:
+) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \)
+) Sử dụng giả thiết \(v(0) = 30\) để tìm hằng số C.
+) Áp dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \)
Lời giải chi tiết:
Ta có \(v\left( t \right) = \int {a\left( t \right)dt} = \int {\frac{{ - 20}}{{{{\left( {1 + 2t} \right)}^2}}}dt} = - \frac{{20}}{2}\frac{{ - 1}}{{1 + 2t}} + C = \frac{{10}}{{1 + 2t}} + C\)
Theo đề bài ta có \(v\left( 0 \right) = 30 \Leftrightarrow \frac{{10}}{{1 + 2.0}} + C = 30 \Leftrightarrow C = 20 \Rightarrow v\left( t \right) = \frac{{10}}{{1 + 2t}} + 20\)
Vậy quãng đường vật đi được sau 2 giây là :
\(S = \int\limits_0^2 {\left( {\frac{{10}}{{1 + 2t}} + 20} \right)dt} = \left. {\left( {5\ln \left( {1 + 2t} \right) + 20t} \right)} \right|_0^2 = 5\ln 5 + 40 = 48\,\,\left( m \right)\)
Chọn C.
Câu hỏi 12 :
Một vật chuyển động với vận tốc \(10\) (m/s) thì tăng tốc với gia tốc \(a(t) = 3t + t^2\)(m/s2). Tính quãng đường mà vật đi được trong khoảng thời gian \(10s\) kể từ lúc bắt đầu tăng tốc (Tính chính xác đến hàng phần trăm).
- A \(483,33 (m)\)
- B \(1333,33 (m)\)
- C \(1433,33 (m)\)
- D \(196,11 (m)\)
Đáp án: C
Phương pháp giải:
+) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \)
+) Sử dụng giả thiết \(v(0) = 10\) để tìm hằng số C.
+) Áp dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \)
Lời giải chi tiết:
Vận tốc của vật khi bắt đầu tăng tốc là \(v\left( t \right) = \int {\left( {3t + {t^2}} \right)dt} = \frac{{3{t^2}}}{2} + \frac{{{t^3}}}{3} + C\)
Mà \(v\left( 0 \right) = 10 \Rightarrow C = 10 \Rightarrow v\left( t \right) = \frac{{3{t^2}}}{2} + \frac{{{t^3}}}{3} + 10\)
Quãng đường mà vật đi được trong khoảng thời gian 10s kể từ thời điểm bắt đầu tăng tốc là \(S\left( t \right) = \int\limits_0^{10} {\left( {\frac{{3{t^2}}}{2} + \frac{{{t^3}}}{3} + 10} \right)dt} = 1433,33\,\,\left( m \right)\)
Chọn C.
Câu hỏi 13 :
Một đám vi trùng tại thời điểm t có số lượng là N(t). Biết rằng \(N'\left( t \right) = \frac{{4000}}{{1 + 0,5t}}\) và lúc đầu đám vi trùng có 250000 con. Hỏi sau 10 ngày số lượng vi trùng là bao nhiêu?
- A \(264334\)
- B \(257167\)
- C \(253583\)
- D \( 255545\)
Đáp án: A
Phương pháp giải:
+) Tính \(N\left( t \right) = \int\limits_{}^{} {N'\left( t \right)dt} \)
+) Sử dụng giả thiết \(N(0) = 25000\) đề tìm hằng số C.
+) Tính \(N(10)\).
Lời giải chi tiết:
Số lượng vi trùng tại thời điểm t là \(N\left( t \right) = \int\limits_{}^{} {N'\left( t \right)dt} = \int\limits_{}^{} {\frac{{4000}}{{1 + 0,5t}}dt} = 8000\ln \left( {1 + 0,5t} \right) + C\)
Mà \(N\left( 0 \right) = C = 250000 \Rightarrow N\left( t \right) = 8000\ln \left( {1 + 0,5t} \right) + 250000\)
Vậy sau 10 ngày số lượng vi trùng là: \(N\left( {10} \right) = 8000\ln \left( {1 + 5} \right) + 250000 = 264334\)
Chọn A.
Câu hỏi 14 :
Trong Vật lí, công được hình thành khi một lực tác động vào một vật và gây ra sự dịch chuyển . Ví dụ như đi xe đạp. Một lực F(x) biến thiên , thay đổi, tác động vào một vật thể làm vật này dịch chuyển từ \(x =a\) đến \(x = b\) thì công sinh ra bởi lực này có thể tính theo công thức \({\rm{W}} = \int\limits_a^b {F(x)} dx\). Với thông tin trên, hãy tính công W sinh ra khi một lực \(F(x) = \sqrt {3x - 2} \) tác động vào một vật thể làm vật này di chuyển từ \(x = 1\) đến \(x = 6\).
- A \(W= 20\)
- B \(W= 12\)
- C \(W= 18\)
- D \(W = 14\)
Đáp án: D
Phương pháp giải:
Sử dụng đúng công thức trong đề bài.
Lời giải chi tiết:
Công W sinh ra khi một lực \(F(x) = \sqrt {3x - 2} \) tác động vào một vật thể làm vật này di chuyển từ x = 1 đến x = 6 là \({\rm{W}} = \int\limits_1^6 {\sqrt {3x - 2} } dx = 14\)
Chọn D.
Câu hỏi 15 :
Thể tích khối tròn xoay thu được khi quay quanh trục \(Ox\) hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{\sqrt{3x+1}}{x+1},\) trục hoành và đường thẳng \(x=1\) là
- A
\(\pi .3\ln 3.\)
- B
\(\pi .\left( 3\ln 3-2 \right).\)
- C
\(3\ln 3-1.\)
- D \(\pi .\left( 3\ln 3-1 \right).\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính thể tích khối tròn xoay và các phương pháp tính tích phân
Lời giải chi tiết:
Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(Ox\) là \(\frac{\sqrt{3x+1}}{x+1}=0\Leftrightarrow 3x+1=0\Leftrightarrow x=-\frac{1}{3}.\)
Suy ra thể tích khối tròn xoay cần tính là \(V=\pi \int\limits_{-\frac{1}{3}}^{1}{{{f}^{2}}\left( x \right)\,\text{d}x}=\pi \int\limits_{-\frac{1}{3}}^{1}{\frac{3x+1}{{{\left( x+1 \right)}^{2}}}\,\text{d}x}\)
Xét tích phân \(I=\int\limits_{0}^{1}{\frac{3x+1}{{{\left( x+1 \right)}^{2}}}\,\text{d}x}=\int\limits_{-\frac{1}{3}}^{1}{\frac{3\left( x+1 \right)-2}{{{\left( x+1 \right)}^{2}}}\,\text{d}x}=\int\limits_{-\frac{1}{3}}^{1}{\left[ \frac{3}{x+1}-\frac{2}{{{\left( x+1 \right)}^{2}}} \right]\text{d}x}\)
\(=\left. \left( 3\ln \left| x+1 \right|+\frac{2}{x+1} \right) \right|_{-\frac{1}{3}}^{1}=3.\ln 2+1-3.\ln \frac{2}{3}-3=3.\ln 3-2.\)
Vậy \(V=\pi \left( 3\ln 3-2 \right).\)
Chọn B
Câu hỏi 16 :
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y=-\,{{x}^{2}}+2x+1\) và \(y=2{{x}^{2}}-4x+1\) là
- A 4
- B 5
- C 8
- D 10
Đáp án: A
Phương pháp giải:
Áp dụng phương pháp tính diện tích hình phẳng của hai đồ thị hàm số \(y=f\left( x \right)\) và \(y=g\left( x \right)\).
Lời giải chi tiết:
Phương trình hoành độ giao điểm của \(\left( {{P}_{1}} \right)\) và \(\left( {{P}_{2}} \right)\) là \(-\,{{x}^{2}}+2x+1=2{{x}^{2}}-4x+1\Leftrightarrow \left[ \begin{align} x=0 \\ x=2 \\ \end{align} \right..\)
Khi đó, diện tích hình phẳng cần tính là \(S=\int\limits_{0}^{2}{\left| -\,{{x}^{2}}+2x+1-2{{x}^{2}}+4x-1 \right|\,\text{d}x}=3\,\int\limits_{0}^{2}{\left| {{x}^{2}}-2x \right|\,\text{d}x}\)
\(=3\,\left| \int\limits_{0}^{2}{\left( {{x}^{2}}-2x \right)\,\text{d}x} \right|=3\,\left| \left. \left( \frac{{{x}^{3}}}{3}-{{x}^{2}} \right) \right|_{0}^{2} \right|=3\left| \frac{{{2}^{3}}}{3}-{{2}^{2}} \right|=3.\frac{4}{3}=4.\)
Vậy diện tích \(S=4.\)
Chọn A
Câu hỏi 17 :
Tính thể tích V của một vật tròn xoay tạo thành khi quay quanh hình phẳng (H) giới hạn bởi các đường \(y={{x}^{2}};\,\,y=\sqrt{x}\) quanh trục Ox.
- A \(V=\frac{7\pi }{10}\).
- B \(V=\frac{9\pi }{10}\).
- C \(V=\frac{3\pi }{10}\).
- D \(V=\frac{\pi }{10}\)
Đáp án: C
Phương pháp giải:
Cho hai hàm số \(y\text{ }=\text{ }f\left( x \right)\)và \(y\text{ }=\text{ }g\left( x \right)\)liên tục trên [a; b]. Khi đó thể tích vật thể tròn xoay giới hạn bởi hai đồ thị số \(y\text{ }=\text{ }f\left( x \right)\), \(y\text{ }=\text{ }g\left( x \right)\)và hai đường thẳng \(x\text{ }=\text{ }a;\text{ }y\text{ }=\text{ }b\)khi quay quanh trục Ox là:
\(V=~\pi \int_{a}^{b}{\left| {{f}^{2}}(x)-{{g}^{2}}(x) \right|dx}\)
Lời giải chi tiết:
Phương trình hoành độ giao điểm của \(y={{x}^{2}};\,\,y=\sqrt{x}\) là: \({{x}^{2}}=\sqrt{x},\,\,\left( x\ge 0 \right)\Leftrightarrow \left[ \begin{align} x=0 \\ x=1 \\ \end{align} \right.\)
Thể tích V của một vật tròn xoay tạo thành khi quay quanh hình phẳng (H) giới hạn bởi các đường \(y={{x}^{2}};\,\,y=\sqrt{x}\) quanh trục Ox là:
\(V=~\pi \int_{0}^{1}{\left| {{\left( {{x}^{2}} \right)}^{2}}-{{\left( \sqrt{x} \right)}^{2}} \right|dx=}\pi \int_{0}^{1}{\left| {{x}^{4}}-x \right|dx=}-\pi \int_{0}^{1}{({{x}^{4}}-x)dx=}=-\pi \left. \left( \frac{{{x}^{5}}}{5}-\frac{{{x}^{2}}}{2} \right)\,\, \right|_{o}^{1}=\frac{3\pi }{10}\)
Chọn: C
Câu hỏi 18 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2}\) và đường thẳng \(y = 2x\) là:
- A \(S = {{20} \over 3}\)
- B \(S = {{496} \over {15}}\)
- C \(S = {4 \over 3}\)
- D \(S = {5 \over 3}\)
Đáp án: C
Phương pháp giải:
Xét phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\), suy ra các nghiệm \(x = a;x = b\)
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \({x^2} = 2x \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 2 \hfill \cr} \right.\)
\( \Rightarrow S = \int\limits_0^2 {\left| {{x^2} - 2x} \right|dx} = \left| {\int\limits_0^2 {\left( {{x^2} - 2x} \right)dx} } \right| = {4 \over 3}\)
Chọn C.
Câu hỏi 19 :
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = 2{x^2} - 4x - 6\), trục hoành độ và hai đường thẳng \(x = - 2,x = - 4\).
- A \(S = 8\)
- B \(S = {{220} \over 3}\)
- C \(S = {{76} \over 3}\)
- D \(S = {{148} \over 3}\)
Đáp án: D
Phương pháp giải:
Phương pháp tìm diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right);y = g\left( x \right);x = a;x = b\):
Bước 1: Xét phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\), tìm các nghiệm thuộc \({x_i} \in \left[ {a;b} \right]\,\,\left( {i = 1;2;3;...;n} \right)\)
Bước 2:
\(\eqalign{ & S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_a^{{x_1}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} + \int\limits_{{x_1}}^{{x_2}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} + ... + \int\limits_{{x_n}}^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \cr & = \left| {\int\limits_a^{{x_1}} {\left( {f\left( x \right) - g\left( x \right)} \right)dx} } \right| + \left| {\int\limits_{{x_1}}^{{x_2}} {\left( {f\left( x \right) - g\left( x \right)} \right)dx} } \right| + ... + \left| {\int\limits_{{x_n}}^b {\left( {f\left( x \right) - g\left( x \right)} \right)dx} } \right| \cr} \)
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm \(2{x^2} - 4x - 6 = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \notin \left[ { - 4; - 2} \right] \hfill \cr x = 3 \notin \left[ { - 4; - 2} \right] \hfill \cr} \right.\)
\( \Rightarrow S = \int\limits_{ - 4}^{ - 2} {\left| {2{x^2} - 4x - 6} \right|dx} = \left| {\int\limits_{ - 4}^{ - 2} {\left( {2{x^2} - 4x - 6} \right)dx} } \right| = {{148} \over 3}\)
Chọn D.
Câu hỏi 20 :
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = \dfrac{1}{2}{x^2} - x\), trục hoành và các đường thẳng \(x = 1;\,\,x = 4\). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích bằng:
- A \(\dfrac{{42\pi }}{5}.\)
- B \(3\pi .\)
- C \(\dfrac{{128\pi }}{{25}}.\)
- D \(\dfrac{{4\pi }}{{15}}.\)
Đáp án: A
Phương pháp giải:
- Xét phương trình hoành độ giao điểm, xác định các nghiệm thuộc \(\left[ {0;4} \right]\).
- Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) khi quanh quay trục hoành là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \(\dfrac{1}{2}{x^2} - x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \notin \left[ {1;4} \right]\\x = 2 \in \left[ {1;4} \right]\end{array} \right.\).
Hình phẳng \(D\) giới hạn bởi đường cong \(y = \dfrac{1}{2}{x^2} - x\), trục hoành và các đường thẳng \(x = 1\), \(x = 4\) có thể tích là:
\(V = \pi \int\limits_1^4 {\left| {{{\left( {\dfrac{1}{2}{x^2} - x} \right)}^2}} \right|dx} = \pi \int\limits_1^4 {{{\left( {\dfrac{1}{2}{x^2} - x} \right)}^2}dx} = \dfrac{{42\pi }}{5}\)
Chọn A.
Câu hỏi 21 :
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2} - 2x\), \(x = 1\), \(x = 4\) và trục hoành.
- A \(S = 6.\)
- B \(S = \dfrac{{22}}{3}.\)
- C \(S = \dfrac{{16}}{3}.\)
- D \(S = \dfrac{{20}}{3}.\)
Đáp án: B
Phương pháp giải:
- Xét phương trình hoành độ giao điểm để tìm các nghiệm thuộc \(\left[ {1;4} \right]\).
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \({x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \notin \left[ {1;4} \right]\\x = 2 \in \left[ {1;4} \right]\end{array} \right.\).
Hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 2x\), \(x = 1\), \(x = 4\) và trục hoành có diện tích bằng:
\(S = \int\limits_1^4 {\left| {{x^2} - 2x} \right|dx} = \left| {\int\limits_1^2 {\left( {{x^2} - 2x} \right)dx} } \right| + \left| {\int\limits_2^4 {\left( {{x^2} - 2x} \right)dx} } \right|\)\( = \left| { - \dfrac{2}{3}} \right| + \left| {\dfrac{{20}}{3}} \right| = \dfrac{{22}}{3}.\)
Chọn B.
Câu hỏi 22 :
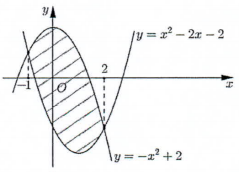
Diện tích phần hình phẳng được gạch chéo trong hình bên bằng
- A \(\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \)
- B \(\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \)
- C \(\int\limits_{ - 1}^2 {\left( { - 2{x^2} - 2x + 4} \right)dx} \)
- D \(\int\limits_{ - 1}^2 {\left( {2{x^2} + 2x - 4} \right)dx} \)
Đáp án: A
Phương pháp giải:
- Xác định hoành độ giao điểm của 2 đồ thị hàm số dựa vào đồ thị đề bài cho.
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) .
- Xét dấu biểu thức trong trị tuyệt đối và phá trị tuyệt đối.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy nghiệm của phương trình hoành độ giao điểm của 2 đồ thị hàm số là \(\left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\).
Do đó diện tích phần gạch chéo là: \(S = \int\limits_{ - 1}^2 {\left| { - {x^2} + 2 - {x^2} + 2x + 2} \right|dx} = \int\limits_{ - 1}^2 {\left| { - 2{x^2} + 2x + 4} \right|dx} \).
Xét trên \(\left[ { - 1;2} \right]\) ta thấy đồ thị hàm số \(y = - {x^2} + 2\) nằm phía trên đồ thị hàm số \(y = {x^2} - 2x - 2\) nên \( - 2{x^2} + 2x + 4 \ge 0\,\,\forall x \in \left[ { - 1;2} \right]\), do đó \(\left| { - 2{x^2} + 2x + 4} \right| = - 2{x^2} + 2x + 4\) \(\forall x \in \left[ { - 1;2} \right]\).
Vậy \(S = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).
Chọn A.
Câu hỏi 23 :
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = \sqrt {2 + \sin x} \), trục hoành và các đường thẳng \(x = 0\), \(x = \pi \). Khối tròn xoay \(D\) tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
- A \(V = 2\left( {\pi + 1} \right)\)
- B \(V = 2\pi \left( {\pi + 1} \right)\)
- C \(V = 2{\pi ^2}\)
- D \(V = 2\pi \)
Đáp án: B
Phương pháp giải:
Thể tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \(\sqrt {2 + \sin x} = 0 \Leftrightarrow \sin x = - 2\) (vô nghiệm).
Khi đó ta có khối tròn xoay \(D\) tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng:
\(\begin{array}{l}V = \pi \int\limits_0^\pi {\left( {2 + \sin x} \right)dx} = \left. {\pi \left( {2x - \cos x} \right)} \right|_0^\pi \\\,\,\,\, = \pi \left( {2\pi + 1 + 1} \right) = 2\pi \left( {\pi + 1} \right)\end{array}\)
Chọn B.
Câu hỏi 24 :
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = x{e^x},\)\(\)\(x = 0,\)\(x = 1\) xung quanh trục \(Ox\) là:
- A \(V = \pi \int\limits_0^1 {{x^2}{e^{2x}}dx.} \)
- B \(V = \pi \int\limits_0^1 {{x^2}{e^x}dx.} \)
- C \(V = \int\limits_0^1 {{x^2}{e^{2x}}dx.} \)
- D \(V = \pi \int\limits_0^1 {x{e^x}dx.} \)
Đáp án: A
Phương pháp giải:
- Xét phương trình hoành độ giao điểm.
- Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) khi quanh quay trục hoành là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \(x{e^x} = 0 \Leftrightarrow x = 0\).
Hình phẳng giới hạn bởi các đường \(y = x{e^x},\) \(y = 0,\) \(x = 0,\) \(x = 1\) xung quanh trục \(Ox\) là:
\(V = \pi \int\limits_0^1 {{{\left( {x{e^x}} \right)}^2}dx} = \pi \int\limits_0^1 {{x^2}{e^{2x}}dx} \)
Chọn A.
Câu hỏi 25 :
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = {x^2};\)\(x = {y^2}\) xung quanh trục \(Ox\) là:
- A \(V = \dfrac{3}{{10}}\)
- B \(V = \dfrac{{3\pi }}{{10}}\)
- C \(V = \dfrac{{10\pi }}{3}\)
- D \(V = \dfrac{{10}}{3}\)
Đáp án: B
Phương pháp giải:
- Xét phương trình hoành độ giao điểm.
- Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) khi quanh quay trục hoành là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \({x^2} = \pm \sqrt x \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right..\)
Thể tích khối tròn xoay là \(V = \pi \int\limits_0^1 {\left| {{x^4} - x} \right|dx} = \dfrac{{3\pi }}{{10}}.\)
Chọn B.
Tổng hợp các bài tập trắc nghiệm ứng dụng tích phân trong hình học mức độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm ứng dụng tích phân trong hình học mức độ nhận biết có đáp án và lời giải chi tiết
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục