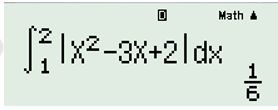25 bài tập ứng dụng tích phân trong hình học mức độ nhận biết
Làm đề thiCâu hỏi 1 :
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f\left( x \right) < 0;\,\,\forall x \in \left[ {a;b} \right].\) Kí hiệu \(S\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\) trục hoành và hai đường thẳng \(x = a,\) \(x = b.\) Khẳng định nào dưới đây sai ?
- A \(S = - \,\int\limits_a^b {f\left( x \right){\rm{d}}x} .\)
- B \(S = \,\int\limits_a^b {f\left( x \right){\rm{d}}x} .\)
- C \(S = \,\int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} .\)
- D \(S = \left| {\,\int\limits_a^b {f\left( x \right){\rm{d}}x} } \right|.\)
Đáp án: B
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \), nhận xét dấu của f(x) trên [a; b] và phá trị tuyệt đối.
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \)
Mặt khác \(f\left( x \right) < 0;\,\,\forall x \in \left[ {a;b} \right] \Rightarrow S = - \,\int\limits_a^b {f\left( x \right)\,{\rm{d}}x} .\)
Chọn B.
Câu hỏi 2 :
Tích diện tích hình phẳng giới hạn bởi \(x = - \,1;\,\,x = 2;\,\,y = 0;\,\,y = {x^2} - 2x.\)
- A \(S = {8 \over 3}.\)
- B \(S = {4 \over 3}.\)
- C \(S = {2 \over 3}.\)
- D \(S = {{16} \over 3}.\)
Đáp án: A
Phương pháp giải:
Xét phương trình hoành độ giao điểm, tìm các nghiệm thuộc [-1;2].
Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \), chia đoạn [-1;2] thành các đoạn nhỏ và tính diện tích hình phẳng
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm \({x^2} - 2x = 0 \Leftrightarrow \left[ \matrix{ x = 0\, \in \left[ { - 1;2} \right] \hfill \cr x = 2 \in \left[ { - 1;2} \right] \hfill \cr} \right.\)
Do đó diện tích hình phẳng cần tính là \(S = \int\limits_{ - \,1}^2 {\left| {{x^2} - 2x} \right|{\rm{d}}x} = \int\limits_{ - \,1}^0 {\left| {{x^2} - 2x} \right|{\rm{d}}x} + \int\limits_0^2 {\left| {{x^2} - 2x} \right|{\rm{d}}x} \)
\( = \left| {\int\limits_{ - \,1}^0 {\left( {{x^2} - 2x} \right){\rm{d}}x} } \right| + \left| {\int\limits_0^2 {\left( {{x^2} - 2x} \right){\rm{d}}x} } \right| = \left| {\left. {\left( {{{{x^3}} \over 3} - {x^2}} \right)} \right|_{ - \,1}^0} \right| + \left| {\left. {\left( {{{{x^3}} \over 3} - {x^2}} \right)} \right|_0^2} \right| = {4 \over 3} + {4 \over 3} = {8 \over 3}.\)
Chọn A.
Câu hỏi 3 :
Kí hiệu \(S\) là diện tích của hình phẳng giới hạn bởi các đường \(y = x\sin x,\,\,y = 0\) và \(x = 0,\,\,x = \pi .\) Khẳng định nào dưới đây đúng ?
- A \(\tan {S \over 3} = 1.\)
- B \(\cos {S \over 2} = 1.\)
- C \(\sin S = 1.\)
- D \(\cos 2S = 1.\)
Đáp án: D
Phương pháp giải:
Xét phương trình hoành độ giao điểm tìm các nghiệm thuộc \(\left[ {0;\pi } \right]\).
Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \)
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm \(x\sin x = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr \sin 0 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = 0 \in \left[ {0;\pi } \right] \hfill \cr x = \pi \in \left[ {0;\pi } \right] \hfill \cr} \right.\)
Diện tích hình phẳng cần tính là \(S = \int\limits_0^\pi {\left| {x.\sin x} \right|{\rm{d}}x} = \int\limits_0^\pi {x.\sin x\,{\rm{d}}x} \) (\(x \in \left[ {0;\pi } \right] \Rightarrow x\sin x > 0\)).
Đặt \(\left\{ \matrix{ u = x \hfill \cr {\rm{d}}v = \sin x\,{\rm{d}}x \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {\rm{d}}u = {\rm{d}}x \hfill \cr v = - \,\cos x \hfill \cr} \right.\,\, \Rightarrow \,\,S = - \,\left. {x.\cos x} \right|_0^\pi + \int\limits_0^\pi {\cos x\,{\rm{d}}x} = \left. {\left( {\sin x - x.\cos x} \right)} \right|_0^\pi = \pi \)
Vậy \(S = \pi \, \Rightarrow \,\,\cos 2S = \cos 2\pi = 1.\)
Chọn D.
Câu hỏi 4 :
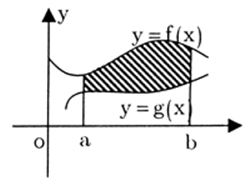
Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành.
Thể tích khối tròn xoay tạo thành được tính theo công thức nào ?
- A \(V=\int\limits_{a}^{b}{{{\left[ f\left( x \right)-g\left( x \right) \right]}^{\,2}}\text{d}x}.\)
- B \(V=\pi .\int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|\text{d}x}.\)
- C \(V=\pi .\int\limits_{a}^{b}{{{\left[ f\left( x \right)-g\left( x \right] \right)}^{\,2}}\text{d}x}.\)
- D \(V=\pi .\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|\text{d}x}.\)
Đáp án: B
Phương pháp giải:
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),y=g\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|\text{d}x}.\)
Lời giải chi tiết:
Thể tích khối tròn xoay được tính theo công thức \(V=\pi .\int\limits_{a}^{b}{\left( {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right)\text{d}x}.\)
Chọn B.
Câu hỏi 5 :
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y=\sqrt{2+\sin x},\) trục hoành và các đường thẳng \(x=0,\,\,x=\pi .\) Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng bao nhiêu ?
- A \(V=2\left( \pi +1 \right).\)
- B \(V=2\pi \left( \pi +1 \right).\)
- C \(V=2{{\pi }^{2}}.\)
- D \(V=2\pi .\)
Đáp án: B
Phương pháp giải:
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\)
Lời giải chi tiết:
Thể tích khối tròn xoay được tính theo công thức \(V=\pi \int\limits_{0}^{\pi }{{{f}^{2}}\left( x \right)\,\text{d}x}.\)
\(=\pi \int\limits_{0}^{\pi }{{{\left( \sqrt{2+\sin x} \right)}^{2}}\,\text{d}x}=\pi \int\limits_{0}^{\pi }{\left( \sin x+2 \right)\,\text{d}x}=\pi \left. \left( 2x-\cos x \right) \right|_{0}^{\pi }=\pi \left( 2\pi +1 \right)+\pi =2\pi \left( \pi +1 \right).\)
Chọn B.
Câu hỏi 6 :
Viết công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \(y=f\left( x \right),\) trục \(Ox\) và hai đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\).
- A \(V=\pi \,\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\,\text{d}x}.\)
- B \(V=\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\,\text{d}x}.\)
- C \(V=\pi \,\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}.\)
- D \(V=\int\limits_{a}^{b}{\left| f\left( x \right) \right|\,\text{d}x}.\)
Đáp án: A
Phương pháp giải:
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\)
Lời giải chi tiết:
Công thức tính thể tích \(V\) cần tìm là \(V=\pi \,\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\,\text{d}x}.\)
Chọn A.
Câu hỏi 7 :
Diện tích hình phẳng giới hạn bởi \(y = \sin x + 1; x = 0; x = {{7\pi } \over 6}\) và trục hoành là \(S\) được biển diễn dưới dạng \({{\sqrt 3 } \over a} + {{7\pi } \over b} + c,\) với \(a,\,\,b,\,\,c \in Z.\) Tính tổng \(T = 3a + 2b + c.\)
- A T=10
- B T=19
- C T=12
- D T=15
Đáp án: B
Phương pháp giải:
Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \)
Lời giải chi tiết:
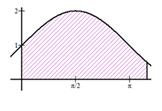
Do \(\sin x + 1 \ge 0;\,\,\forall x \in R\), suy ra diện tích cần tính là:
\(S = \int\limits_0^{{{7\pi } \over 6}} {\left| {\sin x + 1} \right|{\rm{d}}x} = \int\limits_0^{{{7\pi } \over 6}} {\left( {\sin x + 1} \right){\rm{d}}x} = \left. {\left( { - \cos x + x} \right)} \right|_0^{{{7\pi } \over 6}} = {{\sqrt 3 } \over 2} + {{7\pi } \over 6} + 1.\)
Mặt khác \(S = {{\sqrt 3 } \over a} + {{7\pi } \over b} + c\,\,\left( {a,\,\,b,\,\,c \in Z} \right) \Rightarrow \left\{ \matrix{ a = 2 \hfill \cr b = 6 \hfill \cr c = 1 \hfill \cr} \right. \Rightarrow T = 3.2 + 2.6 + 1 = 19.\)
Chọn B.
Câu hỏi 8 :
Cho hàm số \(y = f\left( x \right)\) liên tục trên R và thỏa mãn \(f\left( { - \,1} \right) > 0 > f\left( 0 \right).\) Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),\,\,y = 0,\,\,x = - \,1\) và \(x = 1.\) Mệnh đề nào dưới đây là đúng ?
- A \(S = \int\limits_{ - \,1}^1 {f\left( x \right)\,{\rm{d}}x} .\)
- B \(S = \int\limits_{ - \,1}^0 {f\left( x \right){\rm{d}}x} + \int\limits_0^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} .\)
- C \(S = \left| {\int\limits_{ - \,1}^1 {f\left( x \right){\rm{d}}x} } \right|.\)
- D \(S = \int\limits_{ - \,1}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} .\)
Đáp án: D
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi \(\left\{ \matrix{ y = f\left( x \right),\,\,y = 0 \hfill \cr x = - \,1,\,\,x = 1 \hfill \cr} \right.\) là \(S = \int\limits_{ - \,1}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} .\)
Chọn D.
Câu hỏi 9 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Diện tích hình phẳng phần tô đậm trong hình vẽ là
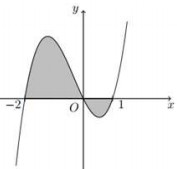
- A \(S = \int\limits_{ - \,2}^0 {f\left( x \right){\rm{d}}x} + \int\limits_0^2 {f\left( x \right){\rm{d}}x} .\)
- B \(S = \int\limits_0^{ - \,2} {f\left( x \right){\rm{d}}x} + \int\limits_0^1 {f\left( x \right){\rm{d}}x} .\)
- C \(S = \int\limits_{ - \,2}^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^1 {f\left( x \right){\rm{d}}x} .\)
- D \(S = \int\limits_{ - \,2}^1 {f\left( x \right){\rm{d}}x} .\)
Đáp án: C
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), x = a, x = b là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \), lưu ý dấu của f(x) trên mỗi đoạn xác định.
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy trên đoạn \(\left\{ \matrix{ x \in \left[ { - \,2;0} \right]\,\, \Rightarrow \,\,f\left( x \right) \ge 0 \hfill \cr x \in \left[ {0;1} \right]\,\, \Rightarrow f\left( x \right) \le 0 \hfill \cr} \right..\)
Khi đó \(S = \int\limits_{ - \,2}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - \,2}^0 {\left| {f\left( x \right)} \right|{\rm{d}}x} + \int\limits_0^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - \,2}^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^1 {f\left( x \right){\rm{d}}x} .\)
Chọn C.
Câu hỏi 10 :
Cho hình phẳng giới hạn bởi \(D=\left\{ y=\tan x;\,\,y=0;\,\,x=0;\,\,x=\frac{\pi }{3} \right\}.\) Thể tích vật tròn xoay khi \(D\) quay quanh trục \(Ox\) là \(V=\pi \left( a-\frac{\pi }{b} \right),\) với \(a,\,\,b\in R.\) Tính \(T={{a}^{2}}+2b.\)
- A \(T=6.\)
- B \(T=9.\)
- C \(T=12.\)
- D \(T=3.\)
Đáp án: B
Phương pháp giải:
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\)
Lời giải chi tiết:
Thể tích vật tròn xoay cần tính là \(V=\pi \int\limits_{0}^{\frac{\pi }{3}}{{{\tan }^{2}}x\,\text{d}x}=\pi \int\limits_{0}^{\frac{\pi }{3}}{\left( \frac{1}{{{\cos }^{2}}x}-1 \right)\,\text{d}x}.\)
\(=\pi \left. \left( \tan x-x \right) \right|_{0}^{\frac{\pi }{3}}=\pi \left( \sqrt{3}-\frac{\pi }{3} \right)=\pi \left( a-\frac{\pi }{3} \right)\,\,\xrightarrow{{}}\,\,\left\{ \begin{align} & a=\sqrt{3} \\ & b=3 \\\end{align} \right..\)
Vậy \(T={{\left( \sqrt{3} \right)}^{2}}+2.3=9.\)
Chọn B.
Câu hỏi 11 :
Bạn Minh ngồi trên máy bay đi du lịch thế giới với vận tốc chuyển động của máy bay là \(v\left( t \right) = 3{t^2} + 5\,\,\left( {m/s} \right)\). Quãng đường máy bay bay từ giây thứ tư đến giây thứ \(10\) là:
- A \(36m\)
- B \(252m\)
- C \(1134m\)
- D \(966m\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \)
Lời giải chi tiết:
Quãng đường máy bay bay từ giây thứ tư đến giây thứ 10 là:
\(S = \int\limits_4^{10} {\left( {3{t^2} + 5} \right)dt} = \left. {\left( {{t^3} + 5t} \right)} \right|_4^{10} = 1050 - 84 = 966\,\,\left( m \right)\)
Chọn D.
Câu hỏi 12 :
Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức \(v\left( t \right) = 3t + 2\), thời gian tính theo đơn vị giây, quãng đường vật đi được tính theo đơn vị m Biết tại thời điểm \(t = 2s\) thì vật đi được quãng đường là 10m. Hỏi tại thời điểm \(t = 30s\) thì vật đi được quãng đường là bao nhiêu?
- A \(1410m\)
- B \(1140m\)
- C \(300m\)
- D \(240m\)
Đáp án: A
Phương pháp giải:
+) Sử dụng công thức \(S = \int\limits_{}^{} {v\left( t \right)dt} \)
+) Sử dụng giả thiết \(S\left( 2 \right) = 10\) để tìm hằng số C.
+) Tính S(30)
Lời giải chi tiết:
Quãng đường đi được tại thời gian t là \(S = \int\limits_{}^{} {\left( {3t + 2} \right)dt} = \frac{{3{t^2}}}{2} + 2t + C\)
Mà \(S\left( 2 \right) = 10 \Rightarrow 6 + 4 + C = 10 \Rightarrow C = 0 \Rightarrow S\left( t \right) = \frac{{3{t^2}}}{2} + 2t\)
Tại thời điểm t = 30s thì vật đi được quãng đường là \(S\left( {30} \right) = \frac{{{{3.30}^2}}}{2} + 2.30 = 1410\,\,\left( m \right)\)
Chọn A.
Câu hỏi 13 :
Một người chạy xe máy chuyển động thẳng theo phương trình \(S\left( t \right) = {t^3} - 3{t^2} + 4t\) trong đó t tính bằng giây (s), S tính bằng mét (m). Gia tốc của xe máy lúc \(t = 2s\) bằng:
- A \(4\) m/s2
- B \(6\) m/s2
- C \(8\) m/s2
- D \(12\) m/s2
Đáp án: B
Phương pháp giải:
+) Sử dụng các công thức \(v\left( t \right) = \left( {S\left( t \right)} \right)',\,a\left( t \right) = \left( {v\left( t \right)} \right)'\)
+) Tính a(2).
Lời giải chi tiết:
Vận tốc tại thời điểm t là: \(v\left( t \right) = \left( {S\left( t \right)} \right)' = 3{t^2} - 6t + 4\)
Gia tốc tại thời điểm t là : \(a\left( t \right) = \left( {v\left( t \right)} \right)' = 6t - 6\)
Suy ra gia tốc tại thời điểm t = 2s là \(a\left( 2 \right) = 6.2 - 6 = 6\,\,\left( {m/{s^2}} \right)\)
Chọn B.
Câu hỏi 14 :
Tính thể tích khi \(S=\left\{ y={{x}^{2}}-4x+6;\,\,y=-\,{{x}^{2}}-2x+6 \right\}\) quay quanh trục \(Ox.\)
- A \(V=3.\)
- B \(V=\dfrac{\pi }{3}.\)
- C \(V=\pi .\)
- D \(V=3\pi .\)
Đáp án: D
Phương pháp giải:
Giải phương trình hoành độ giao điểm của 2 đồ thị hàm số tìm ra các cận x = a và x = b.
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\)
Lời giải chi tiết:
Hoành độ giao điểm của hai parabol là \({{x}^{2}}-4x+6=-\,{{x}^{2}}-2x+6\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=1 \\\end{align} \right..\)
Thể tích vật tròn xoay cần tính là \(V=\pi \int\limits_{0}^{1}{\left| {{\left( {{x}^{2}}-4x+6 \right)}^{2}}-{{\left( -\,{{x}^{2}}-2x+6 \right)}^{2}} \right|\text{d}x}\)
\(=\pi \int\limits_{0}^{1}{\left( 12{{x}^{3}}-36{{x}^{2}}+24x \right)\text{d}x}=\pi \left. \left( 3{{x}^{4}}-12{{x}^{3}}+12{{x}^{2}} \right) \right|_{0}^{1}=3\pi .\)
Chọn D.
Câu hỏi 15 :
Một vật chuyển động với vận tốc ban đầu 5m/s và có gia tốc được xác định bởi công thức \(a = \frac{2}{{t + 1}}\,\left( {m/{s^2}} \right)\). Vận tốc của vật sau 10s đầu tiên là (Làm tròn kết quả đến hàng đơn vị)
- A \(10\) m/s
- B \(9\) m/s
- C \(11\) m/s
- D \(12\) m/s
Đáp án: A
Phương pháp giải:
+) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \)
+) Sử dụng giả thiết \(v\left( 0 \right) = 5\) để tìm hằng số C.
+) Tính v(10) = ?
Lời giải chi tiết:
Ta có \(v\left( t \right) = \int {\dfrac{2}{{t + 1}}dt} = 2\ln \left( {t + 1} \right) + C\)
Mà vận tốc ban đầu là 5 m/s, tức là \(v\left( 0 \right) = 5 \Leftrightarrow 2\ln \left( {0 + 1} \right) + C = 5 \Leftrightarrow C = 5 \Rightarrow v\left( t \right) = 2\ln \left( {t + 1} \right) + 5\)
Vận tốc của vật sau 10s đầu tiên là \(v\left( {10} \right) = 2\ln 11 + 5 \approx 10\,\,\left( {m/s} \right)\)
Chọn A.
Câu hỏi 16 :
Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;\ b \right].\) Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số \(y=f\left( x \right),\) trục hoành và hai đường thẳng \(x=a;\ \ x=b\ \left( a<b \right).\) Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
- A \(V=2\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)
- B \(V={{\pi }^{2}}\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)
- C \(V={{\pi }^{2}}\int\limits_{a}^{b}{f\left( x \right)dx}\)
- D \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)
Đáp án: D
Phương pháp giải:
Thể tích của vật tròn xoay giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục Ox và hai đường thẳng \(x=a;\ \ x=b\ \ \left( a<b \right)\) khi quay quanh trục Ox là: \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)}dx.\)
Lời giải chi tiết:
Theo lý thuyết, chọn đáp án D.
Chọn D.
Câu hỏi 17 :
Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,x=b\left( a<b \right)\). Thể tích của khối của khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành được tính theo công thức:
- A \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)
- B \(V=2\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)
- C \(V={{\pi }^{2}}\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)
- D \(V={{\pi }^{2}}\int\limits_{a}^{b}{f\left( x \right)dx}\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(D\) giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và các đường thẳng \(x=a;x=b\) là \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\).
Lời giải chi tiết:
Công thức tính thể tích khối tròn xoay tạo thành là: \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)
Chọn A.
Câu hỏi 18 :
Viết công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục Ox và hai đường thẳng \(x = a,x = b\,\,\left( {a < b} \right)\) xung quanh trục \(Ox?\)
- A \(V = \int\limits_a^b {{f^2}\left( x \right)dx} \)
- B \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
- C
\(V = \pi \int\limits_a^b {f\left( x \right)dx} \)
- D \(V = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
Đáp án: B
Phương pháp giải:
Dựa vào công thức tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),\,y = g\left( x \right),\,x = a,\,\,x = b\,\,\left( {a < b} \right)\) quanh trục Ox là: \(V = \pi \int\limits_a^b {\left[ {{f^2}\left( x \right) - {g^2}\left( x \right)} \right]} dx\)
Lời giải chi tiết:
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right)\), trục Ox và hai đường thẳng \(x = a,x = b\,\,\left( {a < b} \right)\) xung quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx\)
Chọn B.
Câu hỏi 19 :
Một vật chuyển động chậm dần đều với vận tốc \(v\left( t \right) = 160 - 10t\,\,\left( {m/s} \right)\). Quãng đường mà vật chuyển động từ thởi điểm t = 0(s) đến thời điểm vật dừng lại là:
- A \(1028m\)
- B \(1280m\)
- C \(1308m\)
- D \(1380m\)
Đáp án: B
Phương pháp giải:
+) Tính thời điểm mà vật dừng lại \(\left( {v\left( t \right) = 0} \right)\).
+) Sử dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \)
Lời giải chi tiết:
Khi vật dừng lại ta có \(v\left( t \right) = 160 - 10t = 0 \Rightarrow t = 16\,\,\left( s \right)\)
Vậy quãng đường mà vật chuyển động từ thởi điểm t = 0(s) đến thời điểm vật dừng lại là \(S = \int\limits_0^{16} {\left( {160 - 10t} \right)dt} = 1280\,\,\left( m \right)\)
Chọn B.
Câu hỏi 20 :
Tính diện tích S của hình phẳng giới hạn bởi đường thẳng \(y=2x+1\) và đồ thị hàm số \(y={{x}^{2}}-x+3\)
- A
\(S=\frac{1}{7}\) - B \(S=\frac{1}{8}\)
- C \(S=\frac{1}{6}\)
- D \(S=-\frac{1}{6}\)
Đáp án: C
Phương pháp giải:
Xét phương trình hoành độ giao điểm suy ra các nghiệm \(x=a;\,\,x=b\) , khi đó diện tích cần tính là \(S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|dx}\) .
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm:\(2x+1={{x}^{2}}-x+3\Leftrightarrow {{x}^{2}}-3x+2=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=2 \\ \end{align} \right.\)
\(\Rightarrow S=\int\limits_{1}^{2}{\left| {{x}^{2}}-x+3-2x-1 \right|dx}=\int\limits_{1}^{2}{\left| {{x}^{2}}-3x+2 \right|dx}\), sử dụng MTCT ta có:
Vậy \(S=\frac{1}{6}.\)
Chọn C.
Câu hỏi 21 :
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\left[ a;b \right]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\,\,\left( a<b \right)\) là:
- A \(S=\int\limits_{b}^{a}{\left| f\left( x \right) \right|dx}\)
- B \(S=\int\limits_{a}^{b}{f\left( x \right)dx}\)
- C \(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}\)
- D \(S=\int\limits_{b}^{a}{f\left( x \right)dx}\)
Đáp án: C
Phương pháp giải:
Sử dụng công thức ứng dụng tích phân để tính diện tích hình phẳng.
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\,\,\left( a<b \right)\) là \(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}\).
Chọn C.
Câu hỏi 22 :
Viết công thức tính thể tích \(V\) của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục \(Ox\) tại các điểm \(x = a,\,\,x = b\,\,\,\left( {a < b} \right)\)có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\)\(\left( {a \le x \le b} \right)\) là\(S\left( x \right)\).
- A \(V = {\pi ^2}\int\limits_a^b {\left| {S\left( x \right)} \right|dx} \)
- B \(V = \int\limits_a^b {S\left( x \right)dx} \)
- C \(V = \pi \int\limits_a^b {S\left( x \right)dx} \)
- D \(V = \pi \int\limits_a^b {{S^2}\left( x \right)dx} \)
Đáp án: B
Phương pháp giải:
Công thức tính thể tích \(m = \dfrac{4}{3}\) của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục \(m = \dfrac{1}{3}\) tại các điểm \(m = 1\) có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(\ln \left( {{x^2} + 3x + 1} \right) + {x^2} + 3x < 0\) tại điểm có hoành độ \(0\) là\(2\) là : \(V = \int\limits_a^b {S\left( x \right)dx} \).
Lời giải chi tiết:
Công thức tính thể tích \(m = \dfrac{4}{3}\) của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục \(m = \dfrac{1}{3}\) tại các điểm \(m = 1\) có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(\ln \left( {{x^2} + 3x + 1} \right) + {x^2} + 3x < 0\) tại điểm có hoành độ \(0\) là\(2\) là : \(V = \int\limits_a^b {S\left( x \right)dx} \).
Chọn B.
Câu hỏi 23 :
Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị các hàm số \(y = f\left( x \right),\)\(y = g\left( x \right)\)và các đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\).
- A \(\int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
- B \(\int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)
- C \(\left| {\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\)
- D \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \)
Đáp án: A
Phương pháp giải:
Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số \(y = f\left( x \right),\) \(y = g\left( x \right)\)và các đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số \(y = f\left( x \right),\) \(y = g\left( x \right)\)và các đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Chọn A.
Câu hỏi 24 :
Diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - x\), \(y = 2x - 2\), \(x = 0\), \(x = 3\) được tính bởi công thức:
- A \(S = \left| {\int\limits_0^3 {\left( {{x^2} - 3x + 2} \right)dx} } \right|\)
- B \(S = \int\limits_1^2 {\left| {{x^2} - 3x + 2} \right|dx} \)
- C \(S = \int\limits_0^3 {\left| {{x^2} - 3x + 2} \right|dx} \)
- D \(S = \int\limits_1^2 {\left| {{x^2} + x - 2} \right|dx} \)
Đáp án: C
Phương pháp giải:
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng \(x = a,\;x = b\;\;\left( {a < b} \right)\) và các đồ thị hàm số \(y = f\left( x \right),\;y = g\left( x \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - x;\) \(y = 2x - 2;\) \(x = 0;\) \(x = 3\) được tính bởi công thức:
\(S = \int\limits_0^3 {\left| {{x^2} - x - \left( {2x - 2} \right)} \right|dx} \) \( = \int\limits_0^3 {\left| {{x^2} - 3x + 2} \right|dx.} \)
Chọn C.
Câu hỏi 25 :
Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = - {x^2} + 2x,\,\,y = - 3,\,\,x = 1,\,\,x = 2\) được tính bởi công thức nào dưới đây?
- A \(S = \pi \int\limits_1^2 {{{\left( { - {x^2} + 2x + 3} \right)}^2}dx} \)
- B \(S = \int\limits_1^2 {\left( { - {x^2} + 2x - 3} \right)dx} \)
- C \(S = \int\limits_1^2 {\left( { - {x^2} + 2x + 3} \right)dx} \)
- D \(S = \int\limits_1^2 {\left( {{x^2} - 2x - 3} \right)dx} \)
Đáp án: C
Phương pháp giải:
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng \(x = a,\;x = b\;\;\left( {a < b} \right)\) và các đồ thị hàm số \(y = f\left( x \right),\;y = g\left( x \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} \)
Lời giải chi tiết:
Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = - {x^2} + 2x,\,\,y = - 3,\,\,x = 1,\,\,x = 2\) được tính bởi công thức:
\(S = \int\limits_1^2 {\left| { - {x^2} + 2x + 3} \right|dx} \) \( = \int\limits_1^2 {\left( { - {x^2} + 2x + 3} \right)dx} \)
Chọn C.
Tổng hợp các bài tập trắc nghiệm ứng dụng tích phân trong hình học mức độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm ứng dụng tích phân trong hình học mức độ thông hiểu có đáp án và lời giải chi tiết
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục