Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z=x+yi\)có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay zvào đề bài \(\Rightarrow \)Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử \(w=a+bi\) . Ta có

\(\begin{array}{l}w = (3 + 4i)z + i \Leftrightarrow a + bi = (3 + 4i)z + i \Leftrightarrow a + (b - 1)i = (3 + 4i)z\\ \Leftrightarrow z = \frac{{a + (b - 1)i}}{{3 + 4i}} \Leftrightarrow z = \frac{{\left[ {a + (b - 1)i} \right](3 - 4i)}}{{25}}\\ \Leftrightarrow z = \frac{1}{{25}}[3a + 4b - 4 + ( - 4a + 3b - 3)i]\end{array}\)

 Theo giả thiết cho \(\left| z \right|=4\)  nên ta có

\(\frac{1}{{{25}^{2}}}\left[ {{\left( 3a+4b-4 \right)}^{2}}+{{\left( -4a+3b-3 \right)}^{2}} \right]={{4}^{2}}\)

\(\Leftrightarrow {{(3a+4b-4)}^{2}}+{{(-4a+3b-3)}^{2}}={{100}^{2}}\)

\(\Leftrightarrow 25{{a}^{2}}+25{{b}^{2}}+25-50b={{100}^{2}}\)

\(\Leftrightarrow {{a}^{2}}+{{b}^{2}}-2b+1={{20}^{2}}\)

\(\Leftrightarrow {{a}^{2}}+{{(b-1)}^{2}}={{20}^{2}}\)

Tập hợp các điểm trong mặt phẳng tọa độ \(Oxy\) biểu diễn số phức \(w\) là một đường tròn có bán kính bằng \(20\) .

Chọn A 

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z=x+yi\)có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay zvào đề bài \(\Rightarrow \)Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử \(w=a+bi\) . Ta có

\(\begin{array}{l}w = (1 - i)z + i \Leftrightarrow a + bi = (1 - i)z + i\\ \Leftrightarrow a + bi = (1 - i)(z - 2) + i + 2(1 - i)\\ \Leftrightarrow a + bi = (1 - i)(z - 2) + 2 - i\\ \Leftrightarrow (1 - i)(z - 2) = a - 2 + (b + 1)i\\ \Leftrightarrow z - 2 = \frac{{a - 2 + (b + 1)i}}{{1 - i}}\\ \Leftrightarrow z - 2 = \frac{{\left[ {a - 2 + (b + 1)i} \right](1 + i)}}{2}\\ \Leftrightarrow z - 2 = \frac{1}{2}\left[ {a - 2 - b - 1 + (a - 2 + b + 1)i} \right]\\ \Leftrightarrow z - 2 = \frac{1}{2}\left[ {a - b - 3 + (a + b - 1)i} \right]\end{array}\)

 Theo giả thiết \(\left| z-2 \right|=2\) nên ta có \(\begin{array}{l}\frac{1}{4}\left[ {{{(a - b - 3)}^2} + {{(a + b - 1)}^2}} \right] = 4 \Leftrightarrow {(a - b - 3)^2} + {(a + b - 1)^2} = 16 \Leftrightarrow 2{a^2} + 2{b^2} + 10 - 8a + 4b = 16\\ \Leftrightarrow {a^2} + {b^2} - 4a + 2b - 3 = 0 \Leftrightarrow {(a - 2)^2} + {(b + 1)^2} = 8\end{array}\)

Tập hợp các điểm trong mặt phẳng tọa độ \(Oxy\) biểu diễn số phức \(w\) là một đường tròn có bán kính bằng \(2\sqrt{2}\).

Chọn D 

Phương pháp giải:

Gọi số phức, áp dụng bất đẳng thức Bunhiacopxki để tìm giá trị lớn nhất 

Lời giải chi tiết:

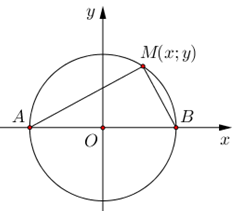
Cách 1. Gọi \(z=x+yi\,\,\left( x,y\in \mathbb{R} \right)\Rightarrow \)\(M\left( x;y \right)\).

Và \(A\left( -\,1;0 \right),\,B\left( 1;0 \right)\).

Ta có \(\left| z \right|=1\Rightarrow \left| x+yi \right|=1\Leftrightarrow {{x}^{2}}+{{y}^{2}}=1.\) \(\Rightarrow M\) thuộc đường tròn đường kính \(AB\). \(\Rightarrow M{{A}^{2}}+M{{B}^{2}}=A{{B}^{2}}=4.\)

Khi đó, theo Bunhiacopxki, ta có \(T=MA+2MB\le \sqrt{\left( {{1}^{2}}+{{2}^{2}} \right)\left( M{{A}^{2}}+M{{B}^{2}} \right)}=\sqrt{5.4}=2\sqrt{5}\)

Vậy giá trị lớn nhất của biểu thức \(\max T=2\sqrt{5}\).

Cách 2. Đặt \(z=x+yi\,\,\left( x,y\in \mathbb{R} \right)\Rightarrow \left| z+1 \right|=\sqrt{{{\left( x+1 \right)}^{2}}+{{y}^{2}}}\) và \(\left| z-1 \right|=\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}}\).

Mặt khác \(\left| z \right|=1\Leftrightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=1\Leftrightarrow {{x}^{2}}+{{y}^{2}}=1\), khi đó \(T=\sqrt{{{\left( x+1 \right)}^{2}}+{{y}^{2}}}+2\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}}\) \(\Leftrightarrow T\le \sqrt{\left( {{1}^{2}}+{{2}^{2}} \right)\left[ {{\left( x+1 \right)}^{2}}+{{y}^{2}}+{{\left( x-1 \right)}^{2}}+{{y}^{2}} \right]}=\sqrt{10\left( {{x}^{2}}+{{y}^{2}}+1 \right)}=2\sqrt{5}\Rightarrow \max T=2\sqrt{5}.\)

Chọn A

Phương pháp giải:

+) Rút z theo w, tìm tập hợp các điểm biểu diễn số phức w.

+) Biểu diễn hình học tất cả các yếu tố có trong bài toán.

+) Tìm điều kiện để P đạt giá trị lớn nhất.

Lời giải chi tiết:

\(z + w = 3 + 4i \Rightarrow z = 3 + 4i - w \Rightarrow \left| {3 + 4i - 2w} \right| = 9 \Leftrightarrow \left| {w - \frac{3}{2} - 2i} \right| = \frac{9}{2}\)

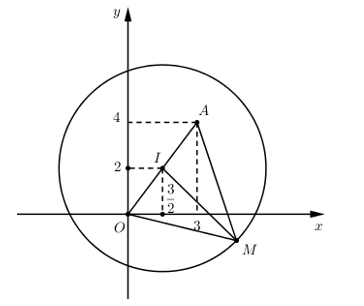
Khi đó tập hợp các điểm biểu diễn số phức w là đường tròn tâm \(I\left( {\frac{3}{2};2} \right)\) bán kính \(R = \frac{9}{2}\).

Ta có: \(T = \left| z \right| + \left| w \right| = \left| {w - 3 - 4i} \right| + \left| w \right|\)

Gọi M là điểm biểu diễn số phức w, \(A\left( {3;4} \right)\) là điểm biểu diễn số phức \(z = 3 + 4i\). Dễ thấy I là trung điểm của OA.

Khi đó \(P = MO + MA\)

\({P_{\max }} \Leftrightarrow OM = OA \Leftrightarrow MI \bot OA\).

Ta có: \(OI = \sqrt {\frac{9}{4} + 4}  = \frac{5}{2}\), \(IM = R = \frac{9}{2}\)

\( \Rightarrow OM = \sqrt {\frac{{25}}{4} + \frac{{81}}{4}}  = \frac{{\sqrt {106} }}{2}\)

\( \Rightarrow {P_{\max }} = 2OM = \sqrt {106} \).

Chọn đáp án D.

Phương pháp giải:

+) Biểu diễn lượng giác của số phức.

+) \(\dfrac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}} = \left| {\dfrac{{{z_1}}}{{{z_2}}}} \right|,\,\,{z_2} \ne 0\)

Lời giải chi tiết:

Cách 1:

Gọi A, B lần lượt là các điểm biểu diễn của số phức \({z_1}\) và \({z_2}\)

Theo đề bài, ta có: \(OA = 3,\,OB = 4,\,AB = \sqrt {41} \)

\( \Rightarrow \cos \widehat {AOB} = \dfrac{{{3^2} + {4^2} - 41}}{{2.3.4}} =  - \dfrac{2}{3}\)

Đặt \({z_1} = 3\left( {\cos \varphi  + i\,\sin \varphi } \right) \Rightarrow {z_2} = 4\left( {\cos \left( {\varphi  \pm \widehat {AOB}} \right) + i\,\sin \left( {\varphi  \pm \widehat {AOB}} \right)} \right) = 4\left( {\cos \left( {\varphi  \pm \alpha } \right) + i\,\sin \left( {\varphi  \pm \alpha } \right)} \right),\,\,\left( {\alpha  = \widehat {AOB}} \right)\)

\( \Rightarrow \dfrac{{{z_1}}}{{{z_2}}} = \dfrac{{3\left( {\cos \varphi  + i\,\sin \varphi } \right)}}{{4\left( {\cos \left( {\varphi  \pm \alpha } \right) + i\,\sin \left( {\varphi  \pm \alpha } \right)} \right)}} = \dfrac{3}{4}.\left( {\cos \varphi  + i\,\sin \varphi } \right)\left( {\cos \left( {\varphi  \pm \alpha } \right) - i\,\sin \left( {\varphi  \pm \alpha } \right)} \right)\)

\( = \dfrac{3}{4}.\left[ {\left( {\cos \varphi .\cos \left( {\varphi  \pm \alpha } \right) + \sin \varphi .\sin \left( {\varphi  \pm \alpha } \right)} \right) + i\left( {\,\sin \varphi .\cos \left( {\varphi  \pm \alpha } \right) - \cos \varphi .\sin \left( {\varphi  \pm \alpha } \right)} \right)} \right]\)

\( = \dfrac{3}{4}.\left[ {\cos \left( { \pm \alpha } \right) + i.\sin \left( { \pm \alpha } \right)} \right] = \dfrac{3}{4}.\left( {\cos \alpha  \pm i\sin \alpha } \right)\)

\( \Rightarrow b =  \pm \dfrac{3}{4}\sin \alpha  \Rightarrow \left| b \right| = \dfrac{3}{4}.\sqrt {1 - {{\left( { - \dfrac{2}{3}} \right)}^2}}  = \dfrac{{\sqrt 5 }}{4}\).

Cách 2:

Ta có: \(\left| {{z_1}} \right| = 3,\,\left| {{z_2}} \right| = 4,\,\left| {{z_1} - {z_2}} \right| = \sqrt {41}  \Rightarrow \left\{ \begin{array}{l}\dfrac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}} = \dfrac{3}{4}\\\dfrac{{\left| {{z_1} - {z_2}} \right|}}{{\left| {{z_2}} \right|}} = \dfrac{{\sqrt {41} }}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {\dfrac{{{z_1}}}{{{z_2}}}} \right| = \dfrac{3}{4}\\\left| {\dfrac{{{z_1}}}{{{z_2}}} - 1} \right| = \dfrac{{\sqrt {41} }}{4}\end{array} \right.\)

\(z = \dfrac{{{z_1}}}{{{z_2}}} = a + bi,\,\,\left( {a,b \in \mathbb{R}} \right)\,\, \Rightarrow \)\(\left\{ \begin{array}{l}{a^2} + {b^2} = {\left( {\dfrac{3}{4}} \right)^2}\\{\left( {a - 1} \right)^2} + {b^2} = {\left( {\dfrac{{\sqrt {41} }}{4}} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} = \dfrac{9}{{16}}\\{\left( {a - 1} \right)^2} + {b^2} = \dfrac{{41}}{{16}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b^2} = \dfrac{9}{{16}} - {a^2}\\{\left( {a - 1} \right)^2} + \dfrac{9}{{16}} - {a^2} = \dfrac{{41}}{{16}}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{b^2} = \dfrac{5}{{16}}\\a =  - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| b \right| = \dfrac{{\sqrt 5 }}{4}\\a =  - \dfrac{1}{2}\end{array} \right.\)

Vậy \(\left| b \right| = \dfrac{{\sqrt 5 }}{4}\).

Chọn: D

Lời giải chi tiết:

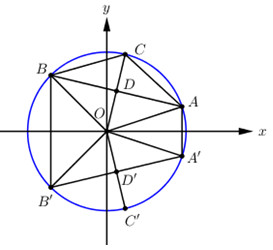
Do \({z_1},\,\,{z_2},\,\,{z_3}\) lần lượt được biểu diễn bởi các điểm \(A,\,\,B,\,\,C\). Gọi \(A',\,\,B',C'\) là các điểm đối xứng \(A,B,C\) qua \(Ox \Rightarrow \) \(A',\,\,B',C'\) lần lượt là các điểm biểu diễn số các số phức \(\overline {{z_1}} ,\,\,\overline {{z_2}} ,\,\,\overline {{z_3}} \) nên theo bài ra ta có: \(\left\{ \begin{array}{l}OA = OB = OC = OA' = OB' = OC' = 3\\\left| {\overrightarrow {OA'}  + \overrightarrow {OB'} } \right| = \left| {\overrightarrow {OC'} } \right| = 3\end{array} \right.\)

Gọi \(D'\) là trung điểm của \(A'B'\) ta có: \(\overrightarrow {OA'}  + \overrightarrow {OB'}  = 2\overrightarrow {OD'}  = \overrightarrow {OC'}  \Rightarrow D'\) là trung điểm của \(OC'\)\( \Rightarrow OD = \dfrac{3}{2}\).

Xét tam giác \(OA'B'\) ta có: \(O{D^2} = \dfrac{{OA{'^2} + OB{'^2}}}{2} - \dfrac{{A'B{'^2}}}{4}\)

\( \Leftrightarrow \dfrac{9}{4} = \dfrac{{9 + 9}}{2} - \dfrac{{A'B{'^2}}}{4} \Rightarrow A'B' = 3\sqrt 3  = AB\).

Áp dụng định lí Cosin trong tam giác \(OAB\) ta có:

\(\cos \angle AOB = \dfrac{{O{A^2} + O{B^2} - A{B^2}}}{{2OA.OB}} = \dfrac{{9 + 9 - 27}}{{2.3.3}} = \dfrac{{ - 1}}{2} \Rightarrow \angle AOB = {120^0}\).

Gọi \(D\) là điểm đối xứng \(D'\) qua \(Ox\). Do \(D'\) là trung điểm của \(A'B'\) nên \(D\) là trung điểm của \(AB\).

\(D'\) là trung điểm của \(OC' \Rightarrow D\) là trung điểm của \(OC\).

Xét tứ giác \(OACB\) có hai đường chéo \(OC,\,\,AB\) cắt nhau tại trung điểm mỗi đường \( \Rightarrow OACB\) là hình bình hành \( \Rightarrow \angle ACB = \angle AOB = {120^0}\).

Chọn C.

Lời giải chi tiết:

Giả sử \(z = x + yi\). Gọi \(A,\,\,B\) lần lượt là các điểm biểu diễn cho số phức \({z_1},\,\,{z_2}\) ta có \(AB = 4\).

Ta có:

\(\begin{array}{l}\left( {z - 6} \right)\left( {8 + \overline {zi} } \right) = \left( {x + yi - 6} \right)\left( {8 + \overline {\left( {x + yi} \right)i} } \right) = \left[ {\left( {x - 6} \right) + yi} \right]\left( {8 - xi - y} \right)\\ = \left[ {\left( {x - 6} \right) + yi} \right]\left[ {\left( {8 - y} \right) - xi} \right] = \left( {x - 6} \right)\left( {8 - y} \right) + xy + \left[ {\left( {8 - y} \right)y - \left( {x + 6} \right)x} \right]i\\ = 8x - xy - 48 + 6y + xy - \left( {{x^2} + {y^2} + 6x - 8y} \right)i\\ = 8x + 6y - 48 - \left( {{x^2} + {y^2} + 6x - 8y} \right)i\end{array}\)

Theo bài ra ta có \({x^2} + {y^2} - 6x - 8y = 0\).

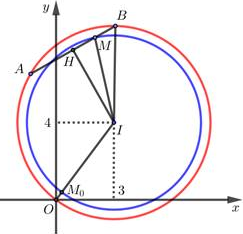
\( \Rightarrow A,B \in \left( C \right):\,\,{x^2} + {y^2} - 6x - 8y = 0\) là đường tròn tâm \(\left( {4;3} \right)\) bán kính \(R = 5\).

Xét điểm \(M\) thỏa mãn \(\overrightarrow {MA}  + 3\overrightarrow {MB}  = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {MO}  + \overrightarrow {OA}  + 3\overrightarrow {MO}  + \overrightarrow {OB}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {OA}  + 3\overrightarrow {OB}  = 4\overrightarrow {OM} \)

Gọi \(H\) là trung điểm của \(AB\) ta có : \(H{I^2} = {R^2} - H{B^2} = 21,\,\,IM = \sqrt {H{I^2} + H{M^2}}  = \sqrt {22} \).

\( \Rightarrow \) M thuộc đường tròn \(\left( T \right)\) tam \(I\left( {3;4} \right)\) bán kính \(R' = \sqrt {22} \).

Ta có : \(\left| {{z_1} + 3{z_2}} \right| = \left| {\overrightarrow {OA}  + 3\overrightarrow {OB} } \right| = \left| {4\overrightarrow {OM} } \right| = 4OM\)

\( \Rightarrow {\left| {{z_1} + 3{z_2}} \right|_{\min }} \Leftrightarrow O{M_{\min }} = \left| {OI - R'} \right| = 5 - \sqrt {22} \).

Vậy \({\left| {{z_1} + 3{z_2}} \right|_{\min }} = 4\left( {5 - \sqrt {22} } \right) = 20 - 4\sqrt {22} \).

Chọn C.

Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

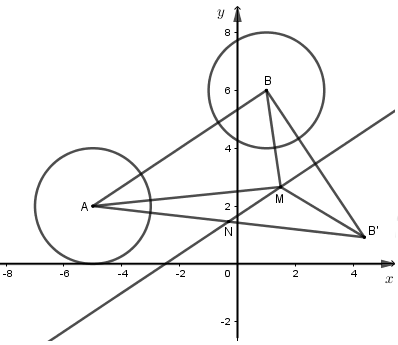
Giả sử \(M,A,B\) lần lượt là các điểm biểu diễn của các số phức \(z,\,\,{z_1} =  - 2 + i,\,\,{z_2} = 2 + 3i\)

Khi đó,  \(\left| {z + 2 - i} \right| - \left| {z - 2 - 3i} \right| = 2\sqrt 5  \Leftrightarrow MA - MB = 2\sqrt 5 \), với \(A\left( { - 2;1} \right),\,B\left( {2;3} \right)\)

Nhận xét: \(AB = \sqrt {{4^2} + {2^2}}  = 2\sqrt 5  \Rightarrow MA - MB = AB \Rightarrow B\) trên đoạn thẳng \(MB\).

\(\begin{array}{l}\overrightarrow {AB}  = \left( {4;2} \right) \Rightarrow \overrightarrow {BM}  = \frac{1}{2}t\overrightarrow {AB} ,\,\,t \ge 0 \Leftrightarrow M\left( {2 + 2t;3 + t} \right)\\ \Rightarrow \left| z \right| = OM = \sqrt {{{\left( {2 + 2t} \right)}^2} + {{\left( {3 + t} \right)}^2}}  = \sqrt {5{t^2} + 14t + 13} ,\,\,t \ge 0.\end{array}\)

Xét \(f\left( t \right) = 5{t^2} + 14t + 13,\,\,t \in \left[ {0; + \infty } \right),\,\,\,\,f'\left( t \right) = 10t + 14 > 0,\,\,\forall t \in \left[ {0; + \infty } \right)\)

\(f\left( t \right)\) liên tục và đồng biến trên \(\left[ {0; + \infty } \right) \Rightarrow \mathop {\min }\limits_{\left[ {0; + \infty } \right)} f\left( t \right) = f\left( 0 \right) = 13\)

\( \Rightarrow {\left| z \right|_{\min }} = \sqrt {13}  \Leftrightarrow t = 0 \Leftrightarrow M\left( {2;3} \right)\,\,\,\left( {M \equiv B} \right).\)

Chọn: C

Lời giải chi tiết:

Theo bài ra ta có :

+) \(\left| z \right| = 2 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \({I_1}\left( {0;0} \right)\) bán kính \({R_1} = 2\). 

\(\left| i \right|\left| {w - \dfrac{{2 - 5i}}{i}} \right| = 1 \Leftrightarrow \left| {w - \left( { - 5 - 2i} \right)} \right| = 1\)

\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(w\) là đường tròn tâm \({I_2}\left( { - 5; - 2} \right)\) bán kính \({R_2} = 1\).

Đặt  \(T = \left| {{z^2} - wz - 4} \right| = \left| {{z^2} - wz - z.\overline z } \right| = \left| z \right|\left| {z - w - \overline z } \right| = 2\left| {z - w - \overline z } \right|\)

Đặt \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi \Rightarrow z - \overline z  = 2bi\).

\( \Rightarrow T = 2\left| {2bi - w} \right|\).

Gọi \(M\left( {0;2b} \right)\) là điểm biểu diễn số phức \(2bi\), \(N\) là điểm biểu diễn số phức \(w\).

\( \Rightarrow T = 2M{N_{\min }} \Leftrightarrow M{N_{\min }}\).

Do \(\left| z \right| = 2 \Rightarrow {a^2} + {b^2} = 4 \Leftrightarrow  - 2 \le b \le 2 \Leftrightarrow  - 4 \le 2b \le 4\).

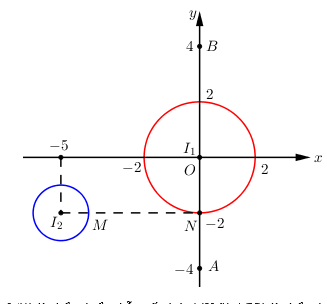
\( \Rightarrow \) Tập hợp các điểm \(M\) là đoạn \(AB\) với \(A\left( { - 4;0} \right),\,\,B\left( {4;0} \right)\).

Dựa vào hình vẽ ta thấy \(M{N_{\min }} = 4 \Leftrightarrow M\left( { - 4; - 2} \right),\,\,N\left( {0; - 2} \right)\).

Vậy \({T_{\min }} = 2.4 = 8\).

Chọn C.

Phương pháp giải:

Áp dụng BĐT Bunhiacopski \({\left( {ax + by} \right)^2}\,\, \le \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right)\)

Dấu “=” xảy ra khi và chỉ khi \(\dfrac{a}{x} = \dfrac{b}{y}\).

Lời giải chi tiết:

Giả sử \(z = a + bi,\,\,\left( {a,b \in \mathbb{R}} \right)\). Do \(\left| {z - 3 - 4i} \right| = \sqrt 5 \) nên \({\left( {a - 3} \right)^2} + {\left( {b - 4} \right)^2} = 5\)

\(M = {\left| {z + 2} \right|^2} - {\left| {z - i} \right|^2} = \left( {{{\left( {a + 2} \right)}^2} + {b^2}} \right) - \left( {{a^2} + {{\left( {b - 1} \right)}^2}} \right) = 4a + 2b + 3 \Rightarrow 4a + 2b + 3 - M = 0\)

Để tồn tại số phức z như trên thì M  thỏa mãn điều kiện: đường thẳng \(4x + 2y + 3 - M = 0\,\,\left( \Delta  \right)\) và đường tròn \({\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 5\) có điểm chung\( \Leftrightarrow d\left( {I;\Delta } \right) \le R\), với \(I\left( {3;4} \right),R = \sqrt 5 \)

\( \Leftrightarrow \dfrac{{\left| {4.3 + 2.4 + 3 - M} \right|}}{{\sqrt {{4^2} + {2^2}} }} \le \sqrt 5  \Leftrightarrow \left| {23 - M} \right| \le 10 \Leftrightarrow 13 \le M \le 33\)

\({M_{\max }} = 33\) khi và chỉ khi \(\left\{ \begin{array}{l}4x + 2y + 3 - 33 = 0\\{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 15 - 2x\\{\left( {x - 3} \right)^2} + {\left( {15 - 2x - 4} \right)^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 5\end{array} \right.\)

\( \Leftrightarrow z = 5 + 5i \Leftrightarrow z + i = 5 + 6i \Rightarrow z + i = \sqrt {25 + 36}  = \sqrt {61} \).

Chọn: A

Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

\(\begin{array}{l}\dfrac{z}{{\sqrt {{a^2} + 1} }} = \dfrac{{i - a}}{{1 - a\left( {a - 2i} \right)}} \Leftrightarrow z = \dfrac{{i - a}}{{1 - {a^2} + 2ai}}\sqrt {{a^2} + 1} \\ \Leftrightarrow z = \dfrac{{i - a}}{{ - {{\left( {a - i} \right)}^2}}}\sqrt {{a^2} + 1}  \Leftrightarrow z = \dfrac{{\sqrt {{a^2} + 1} }}{{a - i}} = \dfrac{{\sqrt {{a^2} + 1} \left( {a + i} \right)}}{{{a^2} - {i^2}}}\\ \Leftrightarrow z = \dfrac{{\sqrt {{a^2} + 1} \left( {a + i} \right)}}{{{a^2} + 1}} \Leftrightarrow z = \dfrac{{a + i}}{{\sqrt {{a^2} + 1} }} = \dfrac{a}{{\sqrt {{a^2} + 1} }} + \dfrac{1}{{\sqrt {{a^2} + 1} }}i\end{array}\)

\(M\) là điểm biểu diễn số phức \(z \Rightarrow M\left( {\dfrac{a}{{\sqrt {{a^2} + 1} }};\dfrac{1}{{\sqrt {{a^2} + 1} }}} \right)\).

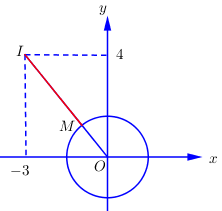
Ta có \({\left( {\dfrac{a}{{\sqrt {{a^2} + 1} }}} \right)^2} + {\left( {\dfrac{1}{{\sqrt {{a^2} + 1} }}} \right)^2} = \dfrac{{{a^2} + 1}}{{{a^2} + 1}} = 1 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \({x^2} + {y^2} = 1\) có tâm \(O\left( {0;0} \right)\) bán kính \(R = 1\).

Khi đó \(I{M_{\min }} = IO - R = \sqrt {{{\left( { - 3} \right)}^2} + {4^2}}  - 1 = 5 - 1 = 4\).

Chọn A

Phương pháp giải:

+) Số phức \(z = x + yi\,\,\,\left( {x;y \in \mathbb{R}} \right)\) có mô đun \(\left| z \right| = \sqrt {{x^2} + {y^2}} \).

+) Sử dụng BĐT Bunhiacopxki với hai bộ số \(\left( {a;b} \right),\,\,\left( {x;y} \right)\) ta có \({\left( {ax + by} \right)^2} \le \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right)\)

+) Dấu “=” xảy ra khi \(\dfrac{x}{a} = \dfrac{y}{b}\)

Lời giải chi tiết:

Gọi số phức \(z = x + yi\,\,\,\left( {x;y \in \mathbb{R}} \right)\)

Theo đề bài \(\left| {z + 1} \right| = \sqrt 3  \Leftrightarrow \left| {x + 1 + yi} \right| = \sqrt 3  \Leftrightarrow {\left( {x + 1} \right)^2} + {y^2} = 3\)

Ta có \(T = \left| {z + 4 - i} \right| + \left| {z - 2 + i} \right| = \left| {x + 4 + \left( {y - 1} \right)i} \right| + \left| {x - 2 + \left( {y + 1} \right)i} \right|\)

\( = \sqrt {{{\left( {x + 4} \right)}^2} + {{\left( {y - 1} \right)}^2}}  + \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y + 1} \right)}^2}} \)

Áp dụng BĐT Bunhiacopxki ta có

 \({T^2} = {\left( {\sqrt {{{\left( {x + 4} \right)}^2} + {{\left( {y - 1} \right)}^2}}  + \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y + 1} \right)}^2}} } \right)^2}\) \( \le \left( {{1^2} + {1^2}} \right)\left[ {{{\left( {x + 4} \right)}^2} + {{\left( {y - 1} \right)}^2} + {{\left( {x - 2} \right)}^2} + {{\left( {y + 1} \right)}^2}} \right]\)

\({T^2} \le 2\left( {2{x^2} + 2{y^2} + 4x + 22} \right) = 4\left( {{{\left( {x + 1} \right)}^2} + {y^2} + 10} \right) = 52\) (vì \({\left( {x + 1} \right)^2} + {y^2} = 3\))

Từ đó \(T \le 2\sqrt {13} \)

Dấu “=” xảy ra khi và chỉ khi:

\(\left\{ \begin{array}{l}{\left( {x + 4} \right)^2} + {\left( {y - 1} \right)^2} = {\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2}\\{\left( {x + 1} \right)^2} + {y^2} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3x + 3\\{\left( {x + 1} \right)^2} + {\left( {3x + 3} \right)^2} = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = \dfrac{3}{{\sqrt {10} }}\\y = \dfrac{9}{{\sqrt {10} }} + 3\end{array} \right.\\\left\{ \begin{array}{l}x =  - \dfrac{3}{{\sqrt {10} }}\\y =  - \dfrac{9}{{\sqrt {10} }} + 3\end{array} \right.\end{array} \right.\)

Vậy \({T_{\max }} = 2\sqrt {13} .\)

Chọn B.

Phương pháp giải:

- Tìm tập hợp điểm biểu diễn các số phức \(z,{z_1},{z_2}\).

- Sử dụng phương pháp hình học nhận xét GTNN của \(T\).

Lời giải chi tiết:

Đặt \(z = x + yi\left( {x,y \in \mathbb{R}} \right)\) ta có:

\(\begin{array}{l}\left| {z - 1 + 2i} \right| = \left| {z + 3 - 4i} \right| \Leftrightarrow {\left| {z - 1 + 2i} \right|^2} = {\left| {z + 3 - 4i} \right|^2}\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = {\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} \Leftrightarrow 2x - 3y + 5 = 0\end{array}\)  

Do đó tập hợp các điểm biểu diễn số phức \(z\) là đường thẳng \(d:2x - 3y + 5 = 0\).

Đặt \({z_1} = {a_1} + {b_1}i,{z_2} = {a_2} + {b_2}i\,\,\,\,\left( {{a_1},{b_1},{a_2},{b_2} \in \mathbb{R}} \right)\)  ta có:

\(\left| {{z_1} + 5 - 2i} \right| = 2 \Leftrightarrow {\left| {{z_1} + 5 - 2i} \right|^2} = 4 \Leftrightarrow {\left( {{a_1} + 5} \right)^2} + {\left( {{b_1} - 2} \right)^2} = 4\)  nên tập hợp điểm biểu diễn số phức \({z_1}\) là đường tròn tâm \(A\left( { - 5;2} \right)\) bán kính \(R = 2\).

\(\left| {{z_2} - 1 - 6i} \right| = 2 \Leftrightarrow {\left| {{z_2} - 1 - 6i} \right|^2} = 4 \Leftrightarrow {\left( {{a_2} - 1} \right)^2} + {\left( {{b_2} - 6} \right)^2} = 4\)  nên tập hợp điểm biểu diễn số phức \({z_2}\) là đường tròn tâm \(B\left( {1;6} \right)\) bán kính \(R = 2\).

Dựng hình:

Gọi điểm \({M_1},{M_2}\) lần lượt biểu diến các số phức \({z_1},{z_2}\) thì:

\(T = \left| {z - {z_1}} \right| + \left| {z - {z_2}} \right| + 4 = M{M_1} + M{M_2} + 4 = \left( {M{M_1} + 2} \right) + \left( {M{M_2} + 2} \right) \ge MA + MB\)

Gọi \(B'\) đối xứng với \(B\) qua \(d\) thì \(MA + MB = MA + MB' \ge AB'\).

Khi đó \(T \ge MA + MB \ge AB'\).

Qua \(B\left( {1;6} \right)\) viết phương trình đường thẳng vuông góc với \(d:2x - 3y + 5 = 0\) ta được \(d':3x + 2y - 15 = 0\).

\(H = d \cap d'\) nên \(H\left( {\frac{{35}}{{13}};\frac{{45}}{{13}}} \right) \Rightarrow B'\left( {\frac{{57}}{{13}};\frac{{12}}{{13}}} \right) \Rightarrow AB' = \frac{{2\sqrt {3770} }}{{13}}\)

Chọn A.

Phương pháp giải:

+) Sử dụng phương pháp hình học.

+) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).

Lời giải chi tiết:

Gọi \(z = x + yi \Rightarrow \overline z  = x - yi\).

Theo bài ra ta có:

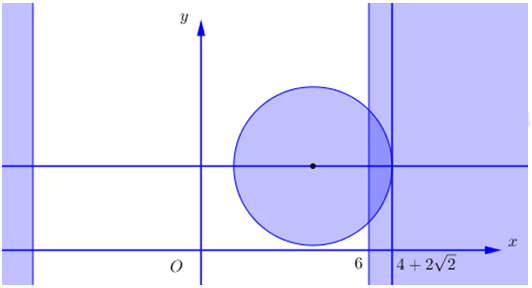
\(\begin{array}{l}\left\{ \begin{array}{l}\left| {z + \overline z } \right| \ge 12\\\left| {z - 4 - 3i} \right| \le 2\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {x + yi + x - yi} \right| \ge 12\\\left| {x - yi - 4 - 3i} \right| \le 2\sqrt 2 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left| {2x} \right| \ge 12\\\sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2}}  \le 2\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge 6\\x \le  - 6\end{array} \right.\\{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} \le 8\end{array} \right.\end{array}\)

Diệnt tích hình (H) là diện tích phần tô đậm hơn.

Ta có \({\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 8 \Leftrightarrow y = 3 \pm \sqrt {8 - {{\left( {x - 4} \right)}^2}} \)

Vậy \(S = 2\int\limits_6^{4 + 2\sqrt 2 } {\left[ {3 + \sqrt {8 - {{\left( {x - 4} \right)}^2}}  - 3} \right]dx}  \approx 2,28\)

Chọn C.

Phương pháp giải:

Chọn điểm rơi: cho số phức \({z_1}\) nhận một giá trị đặc biệt, tìm \({z_2}\) rồi thay vào tìm \(T\).

Lời giải chi tiết:

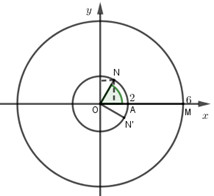
Ta chọn \({z_1} = 6\) có điểm biểu diễn là \(M\left( {6;0} \right)\).

Khi đó \(\widehat {MON} = {60^0}\) nên chọn \(N\left( {1;\sqrt 3 } \right)\) (hình vẽ) biểu diễn số phức \(i{z_2}\)

Suy ra điểm \(N'\left( {\sqrt 3 ; - 1} \right)\) biểu diễn số phức \({z_2}\) hay \({z_2} = \sqrt 3  - i\).

Khi đó \(T = \left| {z_1^2 + 9z_2^2} \right| = \left| {{6^2} + 9{{\left( {\sqrt 3  - i} \right)}^2}} \right| = 36\sqrt 3 \).

Chọn B.

Phương pháp giải:

Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi.\)

Modun của số phức \(z = x + yi:\;\;\left| z \right| = \sqrt {{x^2} + {y^2}} .\)

Lời giải chi tiết:

Ta có:  \({\rm{w}} = \frac{{4 + iz}}{{1 + z}} \Rightarrow {\rm{w}}\left( {1 + z} \right) = 4 + iz \Leftrightarrow z\left( {{\rm{w}} - i} \right) = 4 - {\rm{w}}\)

\( \Rightarrow \sqrt 2 \left| {{\rm{w}} - i} \right| = \left| {4 - {\rm{w}}} \right|.\,\,\,\,\,\left( * \right)\)

Đặt \({\rm{w}} = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right).\)

\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow \sqrt 2 .\sqrt {{x^2} + {{\left( {y - 1} \right)}^2}}  = \sqrt {{{\left( {x - 4} \right)}^2} + {y^2}} \\ \Leftrightarrow 2\left( {{x^2} + {y^2} - 2y + 1} \right) = {x^2} - 8x + 16 + {y^2}\\ \Leftrightarrow {x^2} + {y^2} + 8x - 4y - 14 = 0\\ \Leftrightarrow {x^2} + 8x + 16 + {y^2} - 4y + 4 - 34 = 0\\ \Leftrightarrow {\left( {x + 4} \right)^2} + {\left( {y - 2} \right)^2} = 34\end{array}\)

Vậy tập hợp điểm biểu diễn số phức \({\rm{w}}\) là đường tròn tâm \(\left( { - 4;\,\,2} \right)\) và bán kính \(R = \sqrt {34} .\)

Chọn  A.

Phương pháp giải:

- Đưa các biểu thức trong môđun về dạng hằng đẳng thức \({a^2} - {b^2}\).

- Sử dụng công thức \(\left| {{z_1}.{z_2}} \right| = \left| {{z_1}} \right|.\left| {{z_2}} \right|\).

- Đưa phương trình về dạng tích, chia các trường hợp.

- Đặt \(w = a + bi\), suy ra số phức z, biến đổi và tìm quỹ tích các điểm biểu diễn số phức w.

Lời giải chi tiết:

\(\begin{array}{l}\left| {{z^2} + 2z + 2} \right| = \left| {{z^2} - 2iz - 2} \right|\\ \Leftrightarrow \left| {{z^2} + 2z + 1 + 1} \right| = \left| {{z^2} - 2iz + {i^2} - 1} \right|\\ \Leftrightarrow \left| {{{\left( {z + 1} \right)}^2} - {i^2}} \right| = \left| {{{\left( {z - i} \right)}^2} - {1^2}} \right|\\ \Leftrightarrow \left| {z + 1 - i} \right|\left| {z + 1 + i} \right| = \left| {z - i - 1} \right|\left| {z - i + 1} \right|\\ \Leftrightarrow \left| {z - i + 1} \right|\left( {\left| {z + 1 + i} \right| - \left| {z - i - 1} \right|} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\left| {z - i + 1} \right| = 0\\\left| {z + 1 + i} \right| = \left| {z - i - 1} \right|\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}z = i - 1\\\left| {z + 1 + i} \right| = \left| {z - i - 1} \right|\end{array} \right.\end{array}\)

TH1: \(z = i - 1 \Rightarrow w = i - 1 + 2 - 4i = 1 - 3i\), khi đó \(\left| w \right| = \sqrt {{1^2} + {{\left( { - 3} \right)}^2}}  = \sqrt {10} \).

TH2: \(\left| {z + 1 + i} \right| = \left| {z - i - 1} \right|\) (*).

Đặt \(w = z + 2 - 4i = a + bi\) \( \Rightarrow z = \left( {a - 2} \right) + \left( {b + 4} \right)i\).

Thay vào (*) ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\left| {\left( {a - 2} \right) + \left( {b + 4} \right)i + 1 + i} \right| = \left| {\left( {a - 2} \right) + \left( {b + 4} \right)i - i - 1} \right|\\ \Leftrightarrow \left| {\left( {a - 1} \right) + \left( {b + 5} \right)i} \right| = \left| {\left( {a - 3} \right) + \left( {b + 3} \right)i} \right|\\ \Leftrightarrow {\left( {a - 1} \right)^2} + {\left( {b + 5} \right)^2} = {\left( {a - 3} \right)^2} + {\left( {b + 3} \right)^2}\\ \Leftrightarrow  - 2a + 1 + 10b + 25 =  - 6a + 9 + 6b + 9\\ \Leftrightarrow 4a + 4b + 8 = 0\\ \Leftrightarrow a + b + 2 = 0\end{array}\)

Khi đó tập hợp các điểm biểu diễn số phức w là đường thẳng \(d:\,\,x + y + 2 = 0\).

Gọi \(M\left( {a;b} \right)\) là điểm biểu diễn số phức w, \(M \in d\).

Khi đó ta có \(\left| w \right| = OM \Rightarrow {\left| w \right|_{\min }} \Leftrightarrow O{M_{\min }} = d\left( {O;d} \right)\) \( = \dfrac{{\left| {0 + 0 + 2} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{2}{{\sqrt 2 }} = \sqrt 2 \).

Kết hợp 2 TH ta có \({\left| w \right|_{\min }} = \sqrt 2 \).

Chọn A.

Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

Theo bài ra ta có:

\(\begin{array}{l}\left| {w + i} \right| = \dfrac{{3\sqrt 5 }}{5} \Leftrightarrow \left| {\dfrac{{\left( {2 + i} \right)\left( {z - 4} \right)}}{5} + i} \right| = \dfrac{{3\sqrt 5 }}{5}\\ \Leftrightarrow \dfrac{{\left| {\left( {2 + i} \right)\left( {z - 4} \right) + 5i} \right|}}{5} = \dfrac{{3\sqrt 5 }}{5} \Leftrightarrow \left| {\left( {2 + i} \right)\left( {z - 4} \right) + 5i} \right| = 3\sqrt 5 \\ \Leftrightarrow \left| {\left( {2 + i} \right)z - 8 - 4i + 5i} \right| = 3\sqrt 5  \Leftrightarrow \left| {\left( {2 + i} \right)z - 8 + i} \right| = 3\sqrt 5 \\ \Leftrightarrow \left| {2 + i} \right|.\left| {z + \dfrac{{ - 8 + i}}{{2 + i}}} \right| = 3\sqrt 5  \Leftrightarrow \sqrt 5 \left| {z - 3 + 2i} \right| = 3\sqrt 5 \\ \Leftrightarrow \left| {z - 3 + 2i} \right| = 3\end{array}\)

Suy ra tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \(I\left( {3; - 2} \right)\) bán kính \(R = 3\).

Gọi \(M\) là điểm biểu diễn số phức \(z\); \(A\left( {0;2} \right);\,\,B\left( {6;2} \right)\) lần lượt là các điểm biểu diễn các số phức \(2i;\,\,6 + 2i\).

Yêu cầu bài toán trở thành tìm \(M\) để \(MA + MB\) lớn nhất, \(M\) chạy trên đường tròn  tâm \(I\left( {3; - 2} \right)\) bán kính \(R = 3\).

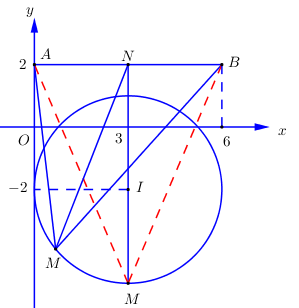
Gọi \(N\) là trung điểm của \(AB \Rightarrow N\left( {3;2} \right)\).

Ta có \({\left( {MA + MB} \right)_{\max }} \Leftrightarrow M{N_{\max }} \Leftrightarrow MN = NI + R = 4 + 3 = 7\). Khi đó \(M\left( {3; - 5} \right)\).

Vậy \({\left( {MA + MB} \right)_{\max }} = 2\sqrt {{3^2} + {7^2}}  = 2\sqrt {58} \).

Chọn C

Phương pháp giải:

- Xác định quỹ tích các điểm biểu diễn số phức \(\overline z \), sử dụng các công thức \(\left| z \right| = \left| {\overline z } \right|,\,\,\overline {z + w}  = \overline z  + \overline w \).

- Biểu diễn hình học và tìm GTLN, GTNN của \(\left| {\overline z  + 1 + i} \right|\).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}\left| {iz - 2i + 1} \right| = 1 \Leftrightarrow \left| {iz - 2i - {i^2}} \right| = 1\\ \Leftrightarrow \left| {i\left( {z - 2 - i} \right)} \right| = 1 \Leftrightarrow \left| i \right|\left| {z - 2 - i} \right| = 1\end{array}\)

\(\begin{array}{l} \Rightarrow \left| {z - 2 - i} \right| = 1 \Rightarrow \left| {\overline {z - 2 - i} } \right| = 1\\ \Leftrightarrow \left| {\overline z  + \overline { - 2 - i} } \right| = 1 \Leftrightarrow \left| {\overline z  - 2 + i} \right| = 1 \Leftrightarrow \left| {\overline z  - \left( {2 - i} \right)} \right| = 1\end{array}\).

Suy ra tập hợp các điểm biểu diễn số phức \(\overline z \) là tâm đường tròn \(\left( C \right)\) tâm \(I\left( {2; - 1} \right)\), bán kính \(R = 1\).

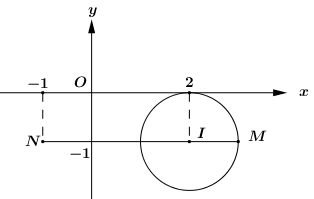
Gọi \(M\) là điểm biểu diễn số phức \(\overline z \), \(N\left( { - 1; - 1} \right)\) là điểm biểu diễn số phức \(z =  - 1 - i\).

Khi đó ta có: \(\left| {\overline z  + 1 + i} \right| = \left| {\overline z  - \left( { - 1 - i} \right)} \right| = MN\) với \(M \in \left( C \right)\).

Ta có: \(\left\{ \begin{array}{l}M{N_{\min }} = IN - R = 3 - 1 = 2\\M{N_{\max }} = IN + R = 3 + 1 = 4\end{array} \right.\) \( \Rightarrow m = 2,\,\,M = 4\).

Vậy \(M + m = 4 + 2 = 6\).

Chọn C.

Phương pháp giải:

- Dựa vào từng giả thiết tìm tập hợp các điểm biểu diễn số phức \(z\).

- Gọi \(M,\,\,A\) lần lượt là các điểm biểu diễn số phức \(z\) và \(2\), khi đó ta có \(\left| {z - 2} \right| = MA\).

- Vẽ hình và tìm vị trí của \(M\) để \(MA\) lớn nhất.

Lời giải chi tiết:

Đặt \(z = a + bi\)\( \Rightarrow \overline z  = a - bi.\)

Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\left( {z - 3 - 3i} \right)\left( {\overline z  - 3 + 3i} \right) = 1\\ \Leftrightarrow \left[ {a - 3 + \left( {b - 3} \right)i} \right]\left[ {a - 3 - \left( {b - 3} \right)i} \right] = 1\\ \Leftrightarrow {\left( {a - 3} \right)^2} - \left( {a - 3} \right)\left( {b - 3} \right)i + \left( {a - 3} \right)\left( {b - 3} \right)i + {\left( {b - 3} \right)^2} = 1\\ \Rightarrow {\left( {a - 3} \right)^2} + {\left( {b - 3} \right)^2} = 1\end{array}\)

\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \(\left( C \right)\) tâm \(I\left( {3;3} \right)\), bán kính \(R = 1\).

Lại theo giả thiết ta có:

\(\begin{array}{l}\,\,\,\,\,\,\left| {\overline z  + 2i} \right| \le \left| {z - 4i} \right|\\ \Leftrightarrow \left| {a - \left( {b - 2} \right)i} \right| \le \left| {a + \left( {b - 4} \right)i} \right|\\ \Leftrightarrow \sqrt {{a^2} + {{\left( {b - 2} \right)}^2}}  \le \sqrt {{a^2} + {{\left( {b - 4} \right)}^2}} \\ \Leftrightarrow {a^2} + {\left( {b - 2} \right)^2} \le {a^2} + {\left( {b - 4} \right)^2}\\ \Leftrightarrow {a^2} + {b^2} - 4b + 4 \le {a^2} + {b^2} - 8b + 16\\ \Leftrightarrow 4b \le 12\\ \Leftrightarrow b \le 3\end{array}\)

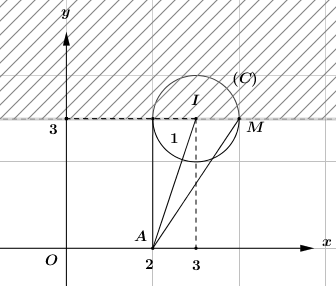
\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn nửa mặt phẳng bờ là đường thẳng \(y = 3\) chứa trục \(Ox\) (Tính cả bờ).

Gọi \(M,\,\,A\) lần lượt là các điểm biểu diễn số phức \(z\) và \(2\), khi đó ta có \(\left| {z - 2} \right| = MA\).

Dựa vào hình vẽ ta thấy \(M{A_{\max }} \Leftrightarrow M\left( {4;3} \right)\). Khi đó \(MA = \sqrt {{2^2} + {3^2}}  = \sqrt {13} \).

Chọn A.