 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Đề ôn tập học kì 1 – Có đáp án và lời giải
Đề ôn tập học kì 1 – Có đáp án và lời giải
Đề số 8 – Đề kiểm tra học kì 1 – Toán 10
Đáp án và lời giải chi tiết Đề số 8 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 10
Đề bài
A. PHẦN TRẮC NGHIỆM: (4 điểm)
Câu 1 : Cho hình bình hành \(ABCD\). Trong các khẳng định sau hãy tìm khẳng định sai ?
A. \(\overrightarrow {AB} = \overrightarrow {DC} \).
B. \(\left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\).
C. \(\overrightarrow {AD} = \overrightarrow {CB} \).
D. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\).
Câu 2 : Tìm tọa độ đỉnh parabol \(y = - 2{x^2} + 4x - 2\).
A. \(I\left( {1;1} \right)\). B. \(I\left( { - 2;2} \right)\).
C. \(I\left( {1;0} \right)\). D. \(I\left( {2;2} \right)\).
Câu 3 : Trong mặt phẳng tọa độ Oxy cho hai vectơ \(\overrightarrow a = (1;2),\,\overrightarrow {\,\,\,b} = ( - 3;5).\,\)Tìm tọa độ của vectơ \(\overrightarrow u = \overrightarrow a - \overrightarrow b .\)
A. \(\overrightarrow u = ( - 4;3).\)
B. \(\overrightarrow u = ( - 2;7).\)
C. \(\overrightarrow u = ( - 3;5).\)
D. \(\overrightarrow u = (4; - 3).\)
Câu 4 : Trong mặt phẳng Oxy, cho \(A(2; - 3),{\rm{ }}B(0;1)\). Tìm tọa độ của vectơ \(\overrightarrow {AB} \).
A. \(\overrightarrow {AB} = \left( {4;2} \right)\).
B. \(\overrightarrow {AB} = \left( {2; - 4} \right)\).
C. \(\overrightarrow {AB} = \left( { - 2;4} \right)\).
D. \(\overrightarrow {AB} = \left( { - 2; - 4} \right)\).
Câu 5 : Trong mặt phẳng Oxy, cho \(A(1; - 1),{\rm{ }}B(2; - 3)\). Tìm tọa độ điểm \(D\) sao cho \(\overrightarrow {AD} = 3\overrightarrow {AB} .\)
A. \(D(4; - 7)\). B. \(D( - 4; - 1)\).
C. \(D(4; - 1)\). D. \(D( - 4;1).\)
Câu 6 : Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AC} = \overrightarrow {BD} \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \).
C. \(\overrightarrow {AB} = \overrightarrow {CD} \).
D. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
Câu 7 : Trong mặt phẳng Oxy, cho \(A(4; - 3),{\rm{ }}B(2; - 1)\). Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(AB\).
A. \(I\left( {2; - 2} \right)\). B. \(I\left( {6; - 4} \right)\).
C. \(I\left( { - 2;2} \right)\). D. \(I\left( {3; - 2} \right)\).
Câu 8 : Cho tập hợp \(A = \left\{ {1;2;4;5} \right\};\,\,B = \left\{ {2;4;6} \right\}\). Xác định tập hợp \(A \cup B\).
A. \(\left\{ {1;2;4;5;6} \right\}\).
B. \(\left\{ {1;5} \right\}\)
C. \(\left\{ {1;2;3;4;5;6} \right\}\).
D. \(\left\{ {2;4} \right\}\).
Câu 9 : Tìm tập xác định của hàm số \(y = \sqrt {3x + 6} \).
A. \(\left( { - \infty ; - 2} \right]\).
B. \(\left[ { - 2; + \infty } \right)\).
C. \(\left[ {2; + \infty } \right)\).
D. \(\left( { - 2; + \infty } \right)\).
Câu 10 : Cho \(\left( P \right):y = - {x^2} + 2x + 3\). Chọn khẳng định đúng ?.
A. Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).
B. Hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;1} \right)\).
C. Hàm số đồng biến trên \(\left( { - 1; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - 1} \right)\).
D. Hàm số đồng biến trên \(\left( { - \infty ; - 1} \right)\)và nghịch biến trên\(\left( { - 1; + \infty } \right)\).
Câu 11 : Hàm số nào sau đây là hàm số chẵn ?
A. \(y = {x^4}\)
B. \(y = {x^4} + 1\).
C. \(y = {x^3}\).
D. \(y = {x^3} + 1.\)
Câu 12 : Cho tập hợp \(A = \left[ { - 2;5} \right);\,\,B = \left( {2;10} \right)\). Xác định tập hợp \(A \cap B\).
A. \(\left[ { - 2;2} \right)\). B. \(\left( {2;5} \right)\).
C. \(\left( {5;10} \right)\). D. \(\left[ { - 2;10} \right)\).
Câu 13 : Cho tập hợp \(A = \left\{ {x \in Z|\left( {x + 4} \right)\left( {{x^2} - 3x + 2} \right) = 0} \right\}\). Viết tập hợp \(A\) bằng cách liệt kê phần tử.
A. \(A = \left\{ {1;2;4} \right\}\).
B. \(A = \left\{ { - 1;2;3} \right\}\).
C. \(A = \left\{ {1;2; - 4} \right\}\).
D. \(A = \left\{ {1;2;3} \right\}\).
Câu 14 : Tìm tập nghiệm của phương trình \(\sqrt {{x^2} - x - 2} = \sqrt {x - 2} \).
A. \(S = \left\{ { - 1;2} \right\}\).
B. \(S = \left\{ 0 \right\}.\)
C. \(S = \left\{ 2 \right\}\).
D. \(S = \left\{ {0;2} \right\}\).
Câu 15 : Tìm tập nghiệm của phương trình \(\sqrt {x - 5} = 2\).
A. \(S = \left\{ 3 \right\}\). B. \(S = \left\{ 9 \right\}\).
C. \(S = \emptyset \). D. \(S = \left\{ 7 \right\}\).
Câu 16 : Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Hỏi \(\overrightarrow {BM} + \overrightarrow {MP} \) bằng vectơ nào?
A. \(\overrightarrow {MN} \) . B. \(\overrightarrow {BA} \).
C. \(\overrightarrow {BC} \). D. \(\overrightarrow {AP} \).
Câu 17 : Tìm trục đối xứng của parabol \(y = 2{x^2} + 4x - 1\).
A. \(x = 1\). B. \(x = 2\).
C. \(x = - 2\). D. \(x = - 1\) .
Câu 18 : Tìm nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y - 3 = 0\\x - 3y + 1 = 0\end{array} \right.\).
A. \(( - 2; - 1)\) B. \((3;1)\).
C. \((2;3)\). D. \((2;1)\).
Câu 19 : Tìm a để đường thẳng \(y = ax - 1\) đi qua điểm \(M\left( {1;3} \right)\).
A. \(a = 2\). B. \(a = 4\).
C. \(a = 1\). D. \(a = 0\).
Câu 20 : Điểm nào dưới đây thuộc đồ thị hàm số \(y = 3x - 1\).
A. \((1;1)\). B. \((2;5)\).
C. \((2;3)\). D. \((0;1)\)
B. PHẦN TỰ LUẬN: (6 điểm)
Bài 1 . (2.0 điểm) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\)
Bài 2 . (1.0 điểm) Giải phương trình \(\sqrt {x - 1} = x - 3\)
Bài 3 . (2.0 điểm) Trong mp Oxy, cho ba điểm \(A\left( {1;1} \right);\,\,B\left( {3;2} \right);\,\,C\left( {4; - 1} \right)\).
a) Tìm tọa độ điểm \(D\) sao cho \(ABCD\) là hình bình hành.
b) Tìm tọa độ điểm \(M\) thỏa mãn \(\overrightarrow {AM} = 2\overrightarrow {AB} - \overrightarrow {BC} \).
Bài 4 . (1.0 điểm) Xác định \(m\) để phương trình \({x^2} + 1 = mx\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa \({x_1} - {x_2} = 1\) (giả sử \({x_1} > {x_2}\)).
Lời giải chi tiết
A. PHẦN TRẮC NGHIỆM
|
1. C |
2. C |
3. D |
4. C |
5. A |
|
6. D |
7. D |
8. A |
9. B |
10. A |
|
11. A |
12.B |
13.C |
14.C |
15. B |
|
16. A |
17.D |
18.D |
19.B |
20. B |
B. PHẦN TỰ LUẬN: (6 điểm)
Bài 1:
+) TXĐ: \(D = R\).
+) Tọa độ đỉnh \(I\left( {2; - 1} \right)\)
+) Trục đối xứng \(x = 2\)
+) Tính biến thiên:
Hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
Hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\).
+) Bảng biến thiên:
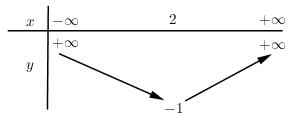
+) Đồ thị:
Giao Ox: Cho \(y = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
Giao Oy: Cho \(x = 0 \Rightarrow y = 3\)
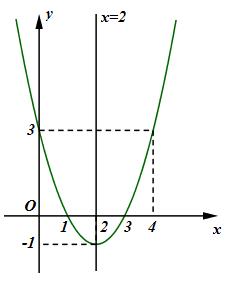
Bài 2:
\(\begin{array}{l}\sqrt {x - 1} = x - 3\\ \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\x - 1 = {\left( {x - 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x - 1 = {x^2} - 6x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} - 7x + 10 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 5\\x = 2\end{array} \right.\end{array} \right. \Leftrightarrow x = 5\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ 5 \right\}\).
Bài 3:
a) Để ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
\(\begin{array}{l} \Leftrightarrow \left( {2;1} \right) = \left( {4 - {x_D}; - 1 - {y_D}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2 = 4 - {x_D}\\1 = - 1 - {y_D}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2\\{y_D} = - 2\end{array} \right.\\ \Rightarrow D\left( {2; - 2} \right)\end{array}\)
Vậy \(D\left( {2; - 2} \right)\).
b) Ta có \(\overrightarrow {AB} = \left( {2;1} \right);\,\,\overrightarrow {BC} = \left( {1; - 3} \right) \\\Rightarrow 2\overrightarrow {AB} - \overrightarrow {BC} = \left( {3;5} \right)\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} = \left( {3;5} \right) \\\Rightarrow \left( {{x_M} - 1;{y_M} - 1} \right) = \left( {3;5} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}{x_M} - 1 = 3\\{y_M} - 1 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 4\\{y_M} = 6\end{array} \right. \\ \Rightarrow M\left( {4;6} \right)\end{array}\).
Vậy \(M\left( {4;6} \right)\).
Bài 4:
\({x^2} + 1 = mx \Leftrightarrow {x^2} - mx + 1 = 0\)
Để phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta = {m^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = 1\end{array} \right.\)
Ta có:
\(\begin{array}{l}{x_1} - {x_2} = 1 \\\Rightarrow {\left( {{x_1} - {x_2}} \right)^2} = 1\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 1\\ \Leftrightarrow {m^2} - 4 = 1 \Leftrightarrow {m^2} = 5 \\\Leftrightarrow m = \pm \sqrt 5 \,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \pm \sqrt 5 \).
Xem lời giải chi tiết đề thi học kì 1 tại Tuyensinh247.com
Loigiaihay.com












Danh sách bình luận