Đề số 7 – Đề kiểm tra học kì 1 – Toán 10

Đề bài

PHẦN TRẮC NGHIỆM

Câu 1 : Biết rằng phương trình \(\sqrt {21x + 190}  = x + 10\) có hai nghiệm phân biệt là a và b. Tính \(P = ab\left( {a + b} \right)\).

A. \(P = 60\)                            B. \(P = 90\)

C. \(P =  - 60\)                         D. \(P =  - 90\)

Câu 2 : Phương trình \({\left( {x + 1} \right)^2} = 3x + 9\) là phương trình hệ quả của phương trình nào sau đây?

A. \(\sqrt {x + 1}  = 3x + 9\)

B. \(\sqrt {x + 1}  = \sqrt {3x - 9} \)

C. \(x + 1 = \sqrt {3x + 9} \)

D. \(x + 1 = 3\left( {x + 3} \right)\)

Câu 3 : Cho một tam giác có độ dài ba cạnh lần lượt là 4cm, 7cm và 9cm. Góc lớn nhất của tam giác có cosin bằng bao nhiêu?

A. \( - \dfrac{{19}}{{21}}\)        B. \(\dfrac{{\sqrt {19} }}{{21}}\)

C. \( - \dfrac{2}{7}\)                 D. \(\dfrac{2}{7}\)

Câu 4 : Biết rằng phương trình \({x^3} - 2{x^2} - 8x + 9 = 0\) có ba nghiệm phân biệt, trong dó có đúng một nghiệm âm có dạng \(\dfrac{{a - \sqrt b }}{c}\) (với a, b, c là các số tự nhiên và phân số \(\dfrac{a}{c}\) tối giản). Tính \(S = a + b + c\).

A. \(S = 40\)                            B. \(S = 38\)

C. \(S = 44\)                            D. \(S = 42\)

Câu 5 : Trong mặt phẳng tọa độ Oxy cho các điểm \(A\left( {1; - 17} \right);\,\,B\left( { - 11; - 25} \right)\). Tìm tọa độ điểm C thuộc BA sao cho \(BC = \sqrt {13} \).

A. \(C\left( { - 8; - 23} \right)\)

B. \(C\left( { - 2; - 19} \right)\)

C. \(C\left( { - 14; - 27} \right)\)

D. \(\left( { - 9; - 22} \right)\)

Câu 6 : Tam giác ABC có \(AB = 4a;\,\,AC = 9a\) và trung tuyến \(AM = \dfrac{{\sqrt {158} a}}{2}\). Tính theo a độ dài của cạnh BC.

A. \(BC = \dfrac{{\sqrt {230} }}{2}a\)

B. \(BC = 6a\)

C. \(BC = 9a\)

D. \(BC = a\sqrt {18} \)

Câu 7 : Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \(2{x^2} - 6x - 3 = 0\). Đặt \(M = \left( {2{x_1} - 1} \right)\left( {2{x_2} - 1} \right)\). Khẳng định nào sau đây là khẳng định đúng?

A. \(M =  - 9\)                          B. \(M =  - 12\)

C. \(M =  - 11\)                        D. \(M =  - 8\)

Câu 8 : Trong mặt phẳng tọa độ Oxy cho các vectơ \(\overrightarrow u  = \left( {3; - 2} \right)\) và \(\overrightarrow v  = \left( {{m^2};4} \right)\) với m là số thực. Tìm m để hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.

A. \(m =  - 6\)

B. \(m =  \pm \sqrt 6 \)

C. \(m = \sqrt 6 \)

D. \(m \in \emptyset \)

Câu 9 : Tìm tập xác định D của phương trình \(\dfrac{{x - 2}}{{{x^2} - 4}} = \sqrt {x - 1} \).

A. \(D = \left[ {1; + \infty } \right)\)

B. \(D = \left[ { - 2;2} \right]\)

C. \(D = \left[ {1; + \infty } \right)\backslash \left\{ 2 \right\}\)

D. \(D = R\backslash \left\{ { \pm 2} \right\}\)

Câu 10 : Tập nghiệm S của phương trình \(3{x^4} - 2{x^2} - 1 = 0\)

A. \(S = \left\{ 1 \right\}\)

B. \(S = \left\{ {1; - \dfrac{1}{3}} \right\}\)

C. \(S = \left\{ { - 1;1} \right\}\)

D. \(S = \left\{ { \pm 1; \pm \dfrac{1}{{\sqrt 3 }}} \right\}\)

Câu 11 : Trong mặt phẳng tọa độ Oxy cho điểm \(A\left( {3; - 7} \right)\) và điểm B. Biết rằng điểm \(M\left( { - 1;2} \right)\) là trung điểm của đoạn thẳng AB. Điểm B không thuộc đường thẳng nào sau đây?

A. \({d_1}:\,\,y = 2x + 11\)

B. \({d_2}:\,\,y = x + 16\)

C. \({d_3}:\,\,y =  - 2x + 1\)

D. \({d_4}:\,\,y =  - x + 6\)

Câu 12 : Cho hình vuông ABCD có \(AB = 2\). Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CA} \) có giá trị bằng bao nhiêu ?

A. \( - 4\)                                 B. \( - 2\)

C. \(2\)                                     D. 4

Câu 13 : Tìm tất cả các giá trị của tham số m để đồ thị \(\left( P \right)\) của hàm số \(y = {x^2} + 2x + m - 2\) cắt trục hoành tại hai điểm phân biệt?

A. \(m < 1\)                             B. \(m > 3\)

C. \(m > 1\)                             D. \(m < 3\)

Câu 14 : Tìm giá trị của m để đỉnh I của đồ thị hàm số \(y = {x^2} - 4x + m\) thuộc đường thẳng \(y = 2017\).

A. \(m = 2019\)                       B. \(m = 2015\)

C. \(m = 2013\)                       D. \(m = 2021\)

Câu 15 : Biết rằng parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\) đi qua hai điểm \(A\left( {1;2} \right)\) và \(B\left( {2;6} \right)\). Tính giá trị của biểu thức \(Q = 3a + b\).

A. \(Q =  - 4\)

B. \(Q = 4\)

C. \(Q = 0\)

D. Không đủ dữ kiện để tính.

Câu 16 : Cho phương trình \(\left( {x + 2} \right)\left( {x - 5} \right) + 3\sqrt {x\left( {x - 3} \right)}  = 0\). Khi đặt \(t = \sqrt {x\left( {x - 3} \right)} \) thì phương trình đã cho trở thanh phương trình nào sau đây?

A. \({t^2} + 3t - 10 = 0\)

B. \({t^2} + 3t + 10 = 0\)

C. \({t^2} - 3t - 10 = 0\)

D. \({t^2} - 3t + 10 = 0\)

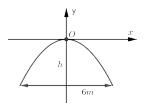
Câu 17 : Một chiếc cổng hình parabol có phương trình \(y =  - \dfrac{1}{2}{x^2}\). Biết cổng có chiều cao \(d = 6\) mét (như hình bên). Hãy tính chiều cao h của cổng?

A. \(h = 5m\)                           B. \(h = 3m\)

C. \(h = 4,5m\)                        D. \(h = 3,5m\)

Câu 18 : Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \(\left| {x - 5} \right| = \left| {3x - 7} \right|\). Tính \(T = \left| {{x_1} - {x_2}} \right|\).

A. \(T = 3\)                              B. \(T = 2\)

C. \(T = 4\)                              D. \(T = 1\)

Câu 19 : Biết rằng hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 5\\mx - 4y = 2\end{array} \right.\) vô nghiệm khi tham số mnhận giá trị bằng \({m_0}\). Khẳng định nào sau đây là khẳng định đúng?

A. \({m_0} \in \left( {\dfrac{1}{2};\dfrac{3}{2}} \right)\)

B. \({m_0} \in \left( { - \dfrac{5}{2}; - \dfrac{3}{2}} \right)\)

C. \({m_0} \in \left( { - \dfrac{3}{2}; - \dfrac{1}{2}} \right)\)

D. \({m_0} \in \left( {\dfrac{3}{2};\dfrac{5}{2}} \right)\)

Câu 20 : Cho tam giác ABC có diện tích bằng 12. Nếu tăng độ dài cạnh AB lên gấp 3 lần, đồng thời giảng độ dài cạnh AC còn một nửa và giữ nguyên độ lớn của góc A thì được một tam giác có diện tích S bằng bao nhiêu?

A. \(S = 18\)                            B. \(S = 16\)

C. \(S = 8\)                              D. \(S = 60\)

PHẦN TỰ LUẬN

Câu 1 (1,0 điểm) : Giải các phương trình:

\(a)\,\,\left| {x - 1} \right| = \left| {{x^2} + 2x} \right|\)              

\(b)\,\,\sqrt {2\left( {x + 1} \right)}  - 2 = \sqrt {x - 1} \)

Câu 2 (1,0 điểm) : Cho phương trình \(\left( {x - 2} \right)\left( {2{x^2} - 2x + 3m - 1} \right) = 0\,\,\left( 1 \right)\) với m là tham số thực.

a) Tìm m để phương trình (1) nhận \({x_0} = 3\) là một nghiệm.

b) Tìm m để phương trình (1) có 3 nghiệm phân biệt trong đó có đúng 1 nghiệm âm.

Câu 3 (1,0 điểm) : Trong mặt phẳng tọa độ Oxy cho tam giác ABC có \(A\left( {2;2} \right);\,\,B\left( {5;3} \right)\) và \(C\left( {4; - 4} \right)\). Chứng minh rằng tam giác ABC vuông và tìm tọa độ điểm D sao cho bốn điểm A, B, C, D lập thành một hình chữ nhật.

Câu 4 (1,0 điểm) : Cho tam giác ABC có \(AC = 7cm,\,\,BC = 10cm\) và \(\widehat {BAC} = {60^0}\). Tính \(\sin \widehat {ABC}\) và tính độ dài cạnh AB (yêu cầu tính ra kết quả chính xác, không tính xấp xỉ).

Lời giải chi tiết

PHẦN TRẮC NGHIỆM

PHẦN TỰ LUẬN

Câu 1:

\(\begin{array}{l}a)\,\,\left| {x - 1} \right| = \left| {{x^2} + 2x} \right|\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = {x^2} + 2x\\x - 1 =  - {x^2} - 2x\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} + x + 1 = 0\,\,\left( \text{vô nghiệm} \right)\\{x^2} + 3x - 1 = 0\end{array} \right.\\ \Leftrightarrow x = \dfrac{{ - 3 \pm \sqrt {13} }}{2}\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ {\dfrac{{ - 3 \pm \sqrt {13} }}{2}} \right\}\).

\(\begin{array}{l}b)\,\,\sqrt {2\left( {x + 1} \right)}  - 2 = \sqrt {x - 1} \\ \Leftrightarrow \sqrt {2\left( {x + 1} \right)}  = 2 + \sqrt {x - 1} \\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\2\left( {x + 1} \right) = 4 + x - 1 + 4\sqrt {x - 1} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x - 1 = 4\sqrt {x - 1} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 2x + 1 = 16x - 16\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 18x + 17 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 17\end{array} \right.\,\,\left( {tm} \right)\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ {1;17} \right\}\).

Câu 2:

a) Thay \(x = 3\) vào phương trình ta có:

\(\left( {3 - 2} \right)\left( {{{2.3}^2} - 2.3 + 3m - 1} \right) = 0 \)

\(\Leftrightarrow 3m + 11 = 0 \Leftrightarrow m =  - \dfrac{{11}}{3}\)

b) \(\left( {x - 2} \right)\left( {2{x^2} - 2x + 3m - 1} \right) = 0 \)

\(\Leftrightarrow \left[ \begin{array}{l}x = 2\\2{x^2} - 2x + 3m - 1 = 0\,\,\,\left( 2 \right)\end{array} \right.\)

Để phương trình (1) có 3 nghiệm phân biệt trong đó có đúng 1 nghiệm âm.

\( \Leftrightarrow \) Phương trình (2) có 2 nghiệm phân biệt trái dấu và khác 2.

\( \Leftrightarrow \left\{ \begin{array}{l}ac = 2\left( {3m - 1} \right) < 0\\{2.2^2} - 2.2 + 3m - 1 \ne 0\end{array} \right.\)

\(\Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{1}{3}\\m \ne  - 1\end{array} \right.\)

\(\Rightarrow m \in \left( { - \infty ;\dfrac{1}{3}} \right)\backslash \left\{ { - 1} \right\}\).

Vậy để phương trình (1) có 3 nghiệm phân biệt trong đó có đúng 1 nghiệm âm thì \(m \in \left( { - \infty ;\dfrac{1}{3}} \right)\backslash \left\{ { - 1} \right\}\).

Câu 3:

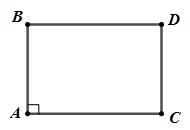
Ta có \(\overrightarrow {AB}  = \left( {3;1} \right);\,\,\overrightarrow {AC}  = \left( {2; - 6} \right);\)\(\,\,\overrightarrow {BC}  = \left( { - 1; - 7} \right)\)

\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC}  = 3.2 + 1.\left( { - 6} \right) = 0\)

\(\Rightarrow AB \bot AC \Rightarrow \Delta ABC\) vuông tại A.

Để ABDC là hình bình hành

\(\begin{array}{l} \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {CD} \\ \Leftrightarrow \left( {3;1} \right) = \left( {{x_D} - 4;{y_D} + 4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 4 = 3\\{y_D} + 4 = 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}{x_D} = 7\\{y_D} =  - 3\end{array} \right. \Rightarrow D\left( {7; - 3} \right)\end{array}\)

Hơn nữa \(\widehat {BAC} = {90^0}\,\,\left( {cmt} \right)\) nên ABDC là hình chữ nhật.

Vậy \(D\left( {7; - 3} \right)\).

Câu 4:

Áp dụng định lí sin ta có:

 \(\begin{array}{l}\dfrac{{AC}}{{\sin \widehat {ABC}}} = \dfrac{{BC}}{{\sin \widehat {BAC}}}\\ \Leftrightarrow \dfrac{7}{{\sin \widehat {ABC}}} = \dfrac{{10}}{{\sin {{60}^0}}}\\ \Leftrightarrow \sin \widehat {ABC} = \dfrac{{7.\sin {{60}^0}}}{{10}} = \dfrac{{7\sqrt 3 }}{{20}}\end{array}\)

Áp dụng định lí cosin ta có:

\(\begin{array}{l}\,\,\,\,\,\,\cos \widehat {BAC} = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}\\ \Leftrightarrow \cos {60^0} = \dfrac{{A{B^2} + {7^2} - {{10}^2}}}{{2.AB.7}}\\ \Leftrightarrow 7AB = A{B^2} - 51\\ \Leftrightarrow A{B^2} - 7AB - 51 = 0\\ \Leftrightarrow \left[ \begin{array}{l}AB = \dfrac{{7 + \sqrt {253} }}{2}\\AB = \dfrac{{7 - \sqrt {253} }}{2} < 0\,\,\left( {ktm} \right)\end{array} \right.\\ \Rightarrow AB = \dfrac{{7 + \sqrt {253} }}{2}\end{array}\)

Xem lời giải chi tiết đề thi học kì 1 tại Tuyensinh247.com

Loigiaihay.com