Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Bài 10. Trung điểm của đoạn thẳng
Bài 64 trang 126 SGK Toán 6 tập 1
cho hai đoạn thẳng AB dài 6cm. Gọi C là trung điểm của AB lấy D và E là hai điểm thuộc đoạn thẳng AB sao cho AD=BE=2cm. Vì sao C là trung điểm của DE?
Đề bài
Cho đoạn thẳng \(AB\) dài \(6cm\). Gọi \(C\) là trung điểm của \(AB\). Lấy \(D\) và \(E\) là hai điểm thuộc đoạn thẳng \(AB\) sao cho \(AD=BE=2cm\). Vì sao \(C\) là trung điểm của \(DE\)?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
C là trung điểm của đoạn thẳng DE khi C nằm giữa D, E và cách đều D, E (CD = CE).
Lời giải chi tiết
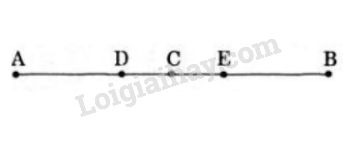
+) Vì \(C\) là trung điểm của \(AB\) nên \(C\) nằm giữa \(A,\) \(B\) và \(CA=CB= AB : 2 = 6:2 = 3(cm)\).
Trên tia \(AB\) có: \(AD < AC\, (2cm<3cm)\) nên điểm \(D\) nằm giữa \(A\) và \(C\), do đó \(AD + DC = AC\)
Suy ra \(CD=AC-AD=3 – 2 = 1 (cm)\).
Trên tia \(BA\) có: \(BE<BC\, (2cm<3cm)\) nên điểm \(E\) nằm giữa \(B\) và \(C\), do đó \(BE + EC = BC\)
Suy ra \(CE=BC-BE=3-2=1cm\).
Ta có: \(CD=1cm\) và \(CE=1cm\) nên \(CD=CE\,(=1cm)\) (1)
+) \(D\) nằm giữa \(A\) và \(C\) nên tia \(CD\) trùng với tia \(CA.\)
\(E\) nằm giữa \(B\) và \(C\) nên tia \(CE\) trùng với tia \(CB.\)
Tia \(CA\) và tia \(CB\) đối nhau nên tia \(CE\) và tia \(CD\) đối nhau. Do đó \(C\) nằm giữa \(D\) và \(E\) (2)
Từ (1) và (2) suy ra \(C\) là trung điểm của \(D\) và \(E.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 65 trang 126 SGK Toán 6 tập 1
- Đề kiểm tra 15 phút - Đề số 1 - Bài 10 - Chương 1 - Hình học 6
- Đề kiểm tra 15 phút - Đề số 2 - Bài 10 - Chương 1 - Hình học 6
- Đề kiểm tra 15 phút - Đề số 3 - Bài 10 - Chương 1 - Hình học 6
- Đề kiểm tra 15 phút - Đề số 4 - Bài 10 - Chương 1 - Hình học 6
>> Xem thêm
Tham Gia Group Dành Cho Lớp 6 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
