 Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
 Bài tập cuối chương 4 Toán 11 kết nối tri thức
Bài tập cuối chương 4 Toán 11 kết nối tri thức
Bài 4.37 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức
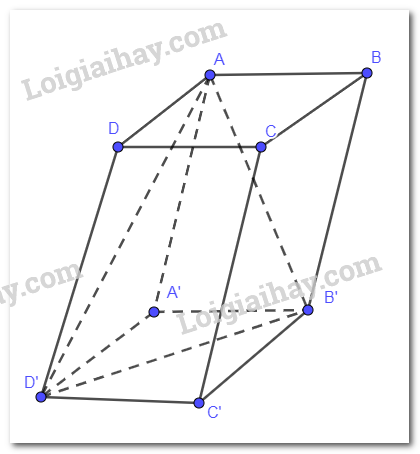
Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’) song song với mặt phẳng A. (ABCD) B. (BCC’B’) C. (BDA’) D. (BDC’)
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’) song song với mặt phẳng
A. (ABCD)
B. (BCC’B’)
C. (BDA’)
D. (BDC’)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) được gọi là song song với nhau nếu chúng không có điểm chung, kí hiệu \(\left( \alpha \right)//\left( \beta \right)\).
Lời giải chi tiết
Vì ABCD.A'B'C'D' là hình hộp nên các mặt của nó là hình bình hành và các cạnh bên AA', BB', CC', DD' đôi một song song và bằng nhau.
Tứ giác BDD'B' có DD' // BB' và DD' = BB' nên BDD'B' là hình bình hành, suy ra B'D' // BD. Do đó, B'D' song song với mặt phẳng (BDC').
Vì A'B'C'D' là hình bình hành nên A'B' // C'D' và A'B' = C'D'.
Vì ABB'A' là hình bình hành nên A'B' // AB và A'B' = AB.
Do đó, AB // C'D' và AB = C'D', suy ra tứ giác ABC'D' là hình bình hành nên BC' // AD'. Do vậy AD' song song với mặt phẳng (BDC').
Mặt phẳng (AB'D') chứa hai đường thẳng cắt nhau B'D' và AD' cùng song song với mặt phẳng (BDC') nên hai mặt phẳng (AB'D') và (BDC') song song với nhau.
Đáp án: D
- Bài 4.38 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.40 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.41 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.42 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức












Danh sách bình luận