Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Bài 6. Tia phân giác của góc
Bài 34 trang 87 SGK Toán 6 tập 2
Vẽ hai góc kề bù xOy và yOx'
Đề bài
Vẽ hai góc kề bù \(xOy\) và \(yOx',\) biết \(\widehat{xOy}=100^0\) . Gọi \(Ot\) là tia phân giác của góc \(xOy\) và \(Ot'\) là tia phân giác của góc \(x'Oy.\) Tính số đo các góc \(x'Ot, xOt', tOt'.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2\)
Lời giải chi tiết
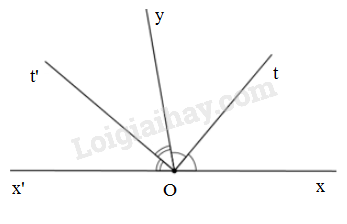
Hai góc \(xOy\) và \(x'Oy\) là hai góc kề bù nên \(\widehat{xOy}+\widehat{x'Oy}=180^0\) mà \(\widehat{xOy}=100^0\) nên \(\widehat{x'Oy}=180^0-\widehat{xOy}\)\(=180^0-100^0=80^0\)
Vì \(Ot\) là tia phân giác của góc \(xOy\) nên \(\displaystyle \widehat {xOt} = \widehat {tOy} = {{\widehat {xOy}} \over 2}\)\( \displaystyle = {{{{100}^0}} \over 2} = {50^0}\)
Vì \(Ot'\) là tia phân giác của góc \(x'Oy\) nên \(\displaystyle \widehat {x'Ot'} = \widehat {t'Oy} \)\(\displaystyle = {{\widehat {x'Oy}} \over 2} = {{{{80}^0}} \over 2} = {40^0}\)
+ Góc \(x'Ot\) và góc \(xOt\) là hai góc kề bù nên \(\widehat {x'Ot} + \widehat {xOt}=180^0\)
Suy ra \(\widehat {x'Ot}=180^0-\widehat {xOt}=180^0-50^0=130^0\)
+ Góc \(xOt'\) và góc \(x'Ot'\) là hai góc kề bù nên \(\widehat {xOt'} + \widehat {x'Ot'}=180^0\)
Suy ra \(\widehat {xOt'}=180^0-\widehat {x'Ot'}=180^0-40^0=140^0\)
+ Vì tia \(Ot'\) nằm giữa hai tia \(Ox'\) và \(Oy,\) tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\)
Lại có hai góc \(xOy\) và \(x'Oy\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ox'\)
Suy ra tia \(Oy\) nằm giữa hai tia \(Ot\) và \(Ot'\)
Do đó \(\widehat {yOt'} + \widehat {yOt}=\widehat {t'Ot}\)
Suy ra \(\widehat {t'Ot}=50^0+40^0=90^0\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 35 trang 87 SGK Toán 6 tập 2
- Bài 36 trang 87 SGK Toán 6 tập 2
- Bài 37 trang 87 SGK Toán 6 tập 2
- Bài 33 trang 87 SGK Toán 6 tập 2
- Bài 32 trang 87 SGK Toán 6 tập 2
>> Xem thêm
Tham Gia Group Dành Cho Lớp 6 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
