Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Bài 6. Tia phân giác của góc
Bài 33 trang 87 SGK Toán 6 tập 2
Vẽ hai góc kề bù xOy, yOx',
Đề bài
Vẽ hai góc kề bù \(xOy, yOx',\) biết \(\widehat{xOy}=130^0\). Gọi \(Ot\) là tia phân giác của góc \(xOy.\) Tính số đo góc \(\widehat{x'Ot}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Hai góc kề bù là hai góc kề nhau và có tổng số đo bằng 180 độ.
+ Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2\)
Lời giải chi tiết
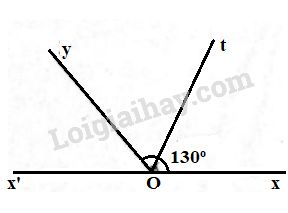
Vì \(Ot\) là tia phân giác của góc \(xOy\) nên:
\(\widehat{xOt} = \widehat {tOy} \)\(= \dfrac{1}2\widehat{xOy}\) \(=\dfrac{130^{0}}2=65^0\)
Vì hai góc \(xOy, yOx'\) kề bù nên \( \widehat {xOy} + \widehat {yOx'} = {180^0}=\widehat {xOx'}\)
Trên cùng một nửa mặt phẳng có bờ là đường thẳng \(xx'\), ta có \(\widehat {xOt}<\widehat {xOx'} \,\,({65^0}<{180^0} )\) nên tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Ox'\)
Do đó:
\(\widehat {xOt} + \widehat {x'Ot} = \widehat {xOx'} \)
\(\Rightarrow \widehat {x'Ot} = \widehat {xOx'} - \widehat {xOt} \)\(= {180^0} - {65^0} = {115^0} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 34 trang 87 SGK Toán 6 tập 2
- Bài 35 trang 87 SGK Toán 6 tập 2
- Bài 36 trang 87 SGK Toán 6 tập 2
- Bài 37 trang 87 SGK Toán 6 tập 2
- Bài 32 trang 87 SGK Toán 6 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
