 Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá
Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá
 Bài 3. Vị trí tương đối của đường thẳng và đường tròn -..
Bài 3. Vị trí tương đối của đường thẳng và đường tròn -..
Lý thuyết Vị trí tương đối của đường thẳng và đường tròn Toán 9 Cùng khám phá
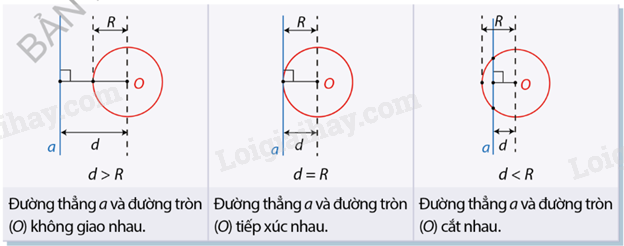
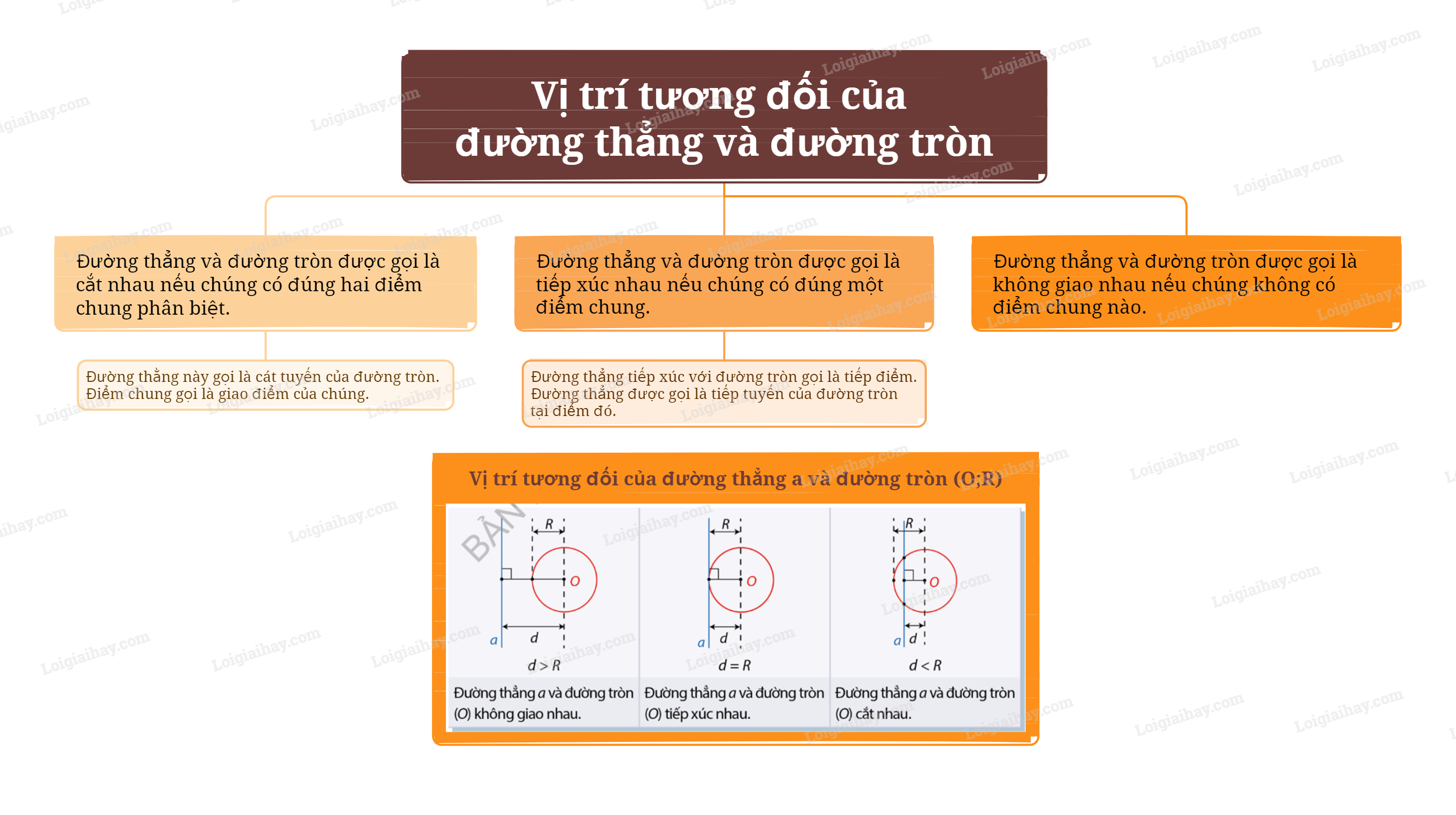
Đường thẳng và đường tròn được gọi là cắt nhau nếu chúng có đúng hai điểm chung phân biệt. Đường thẳng và đường tròn được gọi là tiếp xúc nhau nếu chúng có đúng một điểm chung. Đường thẳng và đường tròn được gọi là không giao nhau nếu chúng không có điểm chung nào.
|
Đường thẳng và đường tròn được gọi là cắt nhau nếu chúng có đúng hai điểm chung phân biệt. Đường thẳng và đường tròn được gọi là tiếp xúc nhau nếu chúng có đúng một điểm chung. Đường thẳng và đường tròn được gọi là không giao nhau nếu chúng không có điểm chung nào. |
Lưu ý:
- Nếu đường thẳng cắt đường tròn thì nó được gọi là cát tuyến của đường tròn. Điểm chung của đường tròn và cát tuyến được gọi là giao điểm của chúng.
- Khi đường thẳng tiếp xúc với đường tròn thì điểm chung của chúng được gọi là tiếp điểm và đường thẳng được gọi là tiếp tuyến của đường tròn tại điểm đó.
Vị trí tương đối của đường thẳng a và đường tròn (O;R) có thể được xác định dựa vào mối quan hệ giữa R và d như trong bảng dưới đây:
- Giải câu hỏi khởi động trang 107 SGK Toán 9 tập 1 - Cùng khám phá
- Giải câu hỏi trang 107, 108, 109 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 5.11 trang 109 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 5.12 trang 110 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 5.13 trang 110 SGK Toán 9 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá












Danh sách bình luận