-
Giải Toán 12 tập 1 - Kết nối tri thức
-
Giải Toán 12 tập 2 - Kết nối tri thức
Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
Bài 6. Vectơ trong không gian - Toán 12 Kết nối tri thức
Lý thuyết Vecto trong không gian Toán 12 Kết nối tri thức
1. Vecto trong không gian
1. Vecto trong không gian
Khái niệm vecto trong không gian
|
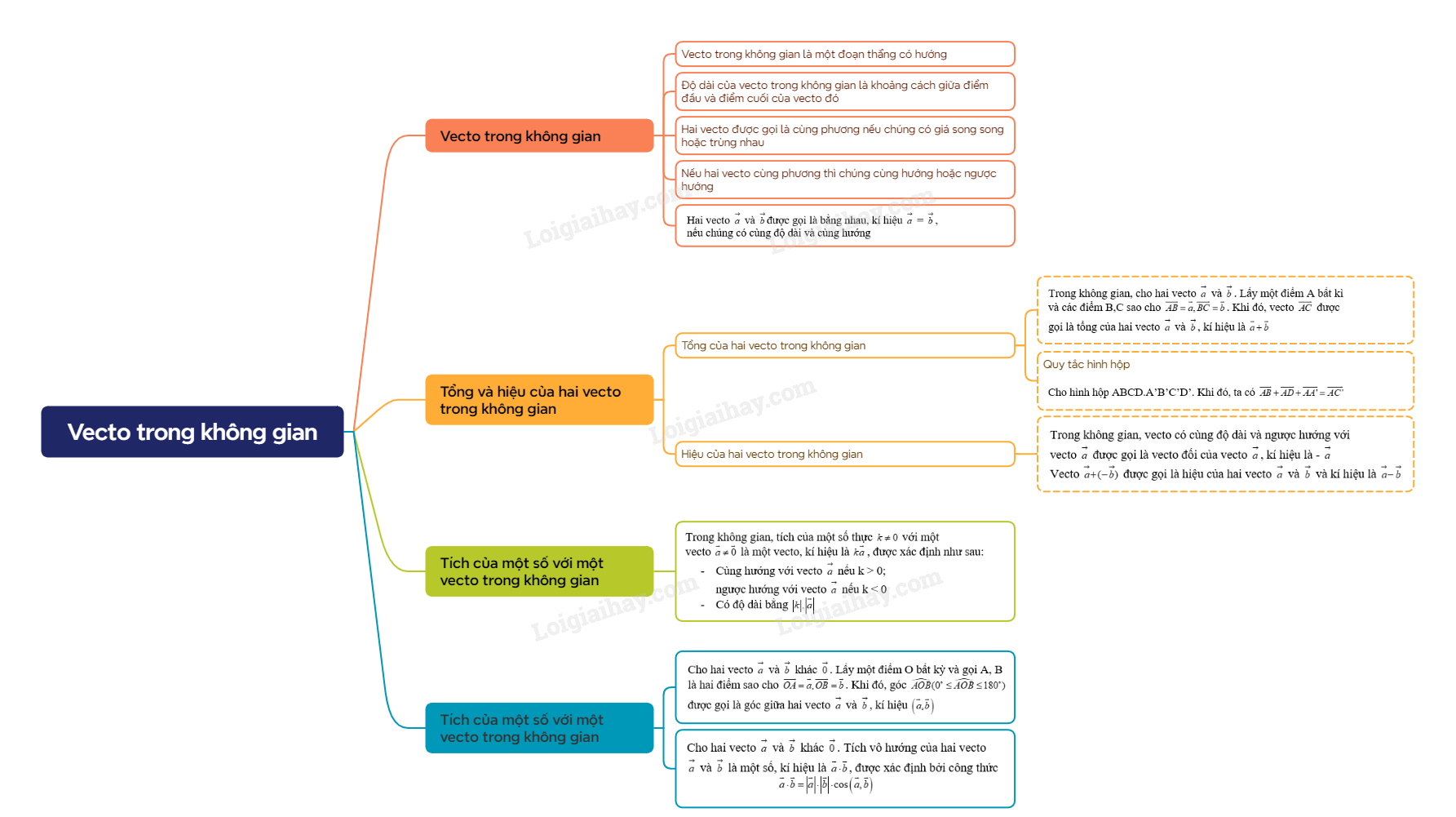
- Vecto trong không gian là một đoạn thẳng có hướng - Độ dài của vecto trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vecto đó - Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau - Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng - Hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \)được gọi là bằng nhau, kí hiệu \(\mathop a\limits^ \to \) = \(\mathop b\limits^ \to \), nếu chúng có cùng độ dài và cùng hướng |
2. Tổng và hiệu của hai vecto trong không gian
a) Tổng của hai vecto trong không gian
|
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \) Trong không gian, phép lấy tổng của hai vecto được gọi là phép cộng vecto |
Quy tắc hình hộp
|
Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \) |
b) Hiệu của hai vecto trong không gian
|
Trong không gian, vecto có cùng độ dài và ngược hướng với vecto \(\mathop a\limits^ \to \) được gọi là vecto đối của vecto \(\mathop a\limits^ \to \), kí hiệu là - \(\mathop a\limits^ \to \) Vecto \(\mathop a\limits^ \to + ( - \mathop b\limits^ \to )\) được gọi là hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) và kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \) Trong không gian, phép lấy hiệu của hai vecto được gọi là phép trừ vecto |
3. Tích của một số với một vecto trong không gian
|
Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau: - Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0 - Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\) Trong không gian, phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto |
4. Tích của một số với một vecto trong không gian
a) Góc giữa hai vecto trong không gian
|
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) |
b) Tích vô hướng của hai vecto trong không gian
|
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) |
Bình luận
Chia sẻ
- Giải mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải mục 2 trang 49, 50, 51 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải mục 3 trang 52, 53, 54 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải mục 4 trang 54, 55, 56 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải bài tập 2.12 trang 59 SGK Toán 12 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Kết nối tri thức - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Phương sai và độ lệch chuẩn Toán 12 Kết nối tri thức
- Lý thuyết Khoảng biến thiên và khoảng tứ phân vị Toán 12 Kết nối tri thức
- Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Kết nối tri thức
- Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức
- Lý thuyết Vecto trong không gian Toán 12 Kết nối tri thức
- Lý thuyết Phương sai và độ lệch chuẩn Toán 12 Kết nối tri thức
- Lý thuyết Khoảng biến thiên và khoảng tứ phân vị Toán 12 Kết nối tri thức
- Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Kết nối tri thức
- Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức
- Lý thuyết Vecto trong không gian Toán 12 Kết nối tri thức
