Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức Bài 6. Vectơ trong không gian - Toán 12 Kết nối tri thức

Giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức


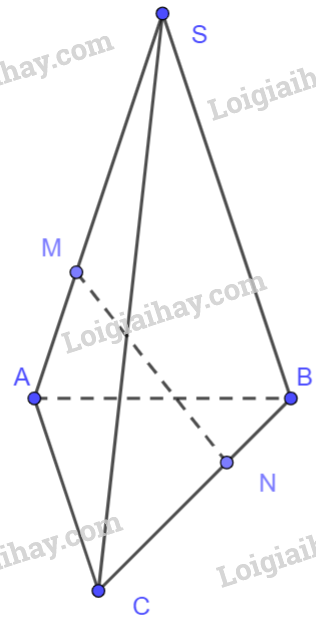
Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho \(SM = 2AM\). Trên cạnh BC, lấy điểm N sao cho \(CN = 2BN\). Chứng minh rằng \(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \).

Đề bài

Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho \(SM = 2AM\). Trên cạnh BC, lấy điểm N sao cho \(CN = 2BN\). Chứng minh rằng \(\overrightarrow {MN}  = \frac{1}{3}\left( {\overrightarrow {SA}  + \overrightarrow {BC} } \right) + \overrightarrow {AB} \).

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a  \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:

- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).

- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).

Lời giải chi tiết

Ta có: \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} = \frac{1}{3}\overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {BC} + \frac{2}{3}\overrightarrow {CB} \)

\( = \frac{1}{3}\overrightarrow {SA} + \overrightarrow {BC} - \frac{2}{3}\overrightarrow {BC} + \overrightarrow {AB} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \) (đpcm)

Ta có: \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} = \frac{1}{3}\overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {BC} + \frac{2}{3}\overrightarrow {CB} \)

\( = \frac{1}{3}\overrightarrow {SA} + \overrightarrow {BC} - \frac{2}{3}\overrightarrow {BC} + \overrightarrow {AB} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \) (đpcm)

 


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua