 Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
 Bài 6. Vectơ trong không gian - Toán 12 Kết nối tri thức
Bài 6. Vectơ trong không gian - Toán 12 Kết nối tri thức
Giải mục 3 trang 52, 53, 54 SGK Toán 12 tập 1 - Kết nối tri thức
Tích của một số với một vectơ trong không gian
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 52 SGK Toán 12 Kết nối tri thức
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)
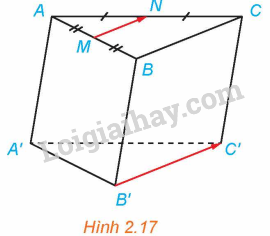
a) Hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương không? Có cùng hướng không?
b) Giải thích vì sao \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
Phương pháp giải:
a) Sử dụng kiến thức về hai vectơ cùng phương để chứng minh: Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
b) Sử dụng kiến thức về độ dài của vectơ trong không gian để chứng minh: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
a) Vì MN là đường trung bình của tam giác ABC nên MN//BC.
Vì BCC’B’ là hình bình hành nên BC//B’C’. Suy ra: MN//B’C’.
Do đó hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương và cùng hướng.
b) Vì BCC’B’ là hình bình hành nên \(BC = B'C'\)
Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}BC\)
Suy ra: \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
CH
Trả lời câu hỏi Câu hỏi trang 53 SGK Toán 12 Kết nối tri thức
Hai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau không? Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) có bằng nhau không?
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \) nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Hai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) bằng nhau vì chúng có cùng độ dài và cùng hướng.
Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) bằng nhau chúng có cùng độ dài và cùng hướng.
LT7
Trả lời câu hỏi Luyện tập 7 trang 53 SGK Toán 12 Kết nối tri thức
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB\). Chứng minh rằng \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \).
Phương pháp giải:
+ Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
+ Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \) nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:

Ta có \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\left( { = \frac{1}{3}} \right)\).
Xét tam giác SAB có: \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\) nên FE // AB và \(EF = \frac{1}{3}AB\) (theo định lí Thales).
Vì hai vectơ \(\overrightarrow {EF} \) và \(\overrightarrow {AB} \) cùng hướng nên \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AB} \) (1)
Vì ABCD là hình bình hành nên \(AB = CD\) và AB // CD. Do đó, \(\overrightarrow {AB} = \overrightarrow {DC} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \).
LT8
Trả lời câu hỏi Luyện tập 8 trang 54 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho \(\overrightarrow {AI} = 3\overrightarrow {IG} \) (H.2.19). Chứng minh rằng \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:

Theo ví dụ 8 ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \)
\(= 3\overrightarrow {AG} \)\( \Rightarrow \overrightarrow {AI} + \overrightarrow {IB} + \overrightarrow {AI} + \overrightarrow {IC} + \overrightarrow {AI} + \overrightarrow {ID} = 3\overrightarrow {AG} \)
\( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 3\overrightarrow {AG} - 3\overrightarrow {AI} \)
\(= 3\left( {\overrightarrow {AG} + \overrightarrow {IA} } \right) = 3\overrightarrow {IG} = \overrightarrow {AI} \)
\( \Rightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \).
VD8
Trả lời câu hỏi Vận dụng 3 trang 54 SGK Toán 12 Kết nối tri thức
Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900km/h lên 920km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900km/h và 920km/h lần lượt được biểu diễn bởi hai vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \). Hãy giải thích vì sao \(\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó. Tính giá trị của k (làm tròn kết quả đến chữ số thập phân thứ hai).

Phương pháp giải:
Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để giải bài toán: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Vì trong quá trình máy bay tăng vận tốc từ 900 km/h lên 920 km/h máy bay giữ nguyên hướng bay nên vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có cùng hướng. Do đó, \(\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó (1).
Gọi \({v_1},{v_2}\) lần lượt là vận tốc của của chiếc máy bay khi đạt 900 km/h và 920 km/h.
Suy ra \({v_1} = 900\) (km/h),{v_2} = 920\) (km/h).
Vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay nên:
\(\frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{\left| {\overrightarrow {{F_2}} } \right|}} = \frac{{v_1^2}}{{v_2^2}} = \frac{{{{900}^2}}}{{{{920}^2}}} = \frac{{2025}}{{2116}} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = \frac{{2025}}{{2116}}\left| {\overrightarrow {{F_2}} } \right|\) (2)
Từ (1) và (2) ta có: \(\overrightarrow {{F_1}} = \frac{{2025}}{{2116}}\overrightarrow {{F_2}} \Rightarrow k = \frac{{2025}}{{2116}} \approx 0,96\).
- Giải mục 4 trang 54, 55, 56 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải bài tập 2.1 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải bài tập 2.3 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức
- Giải bài tập 2.4 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức












Danh sách bình luận